Właściwości transformacji liniowych, jakie są zastosowanie, typy, przykłady

A Transformacja liniowa, które po prostu zadzwonimy, relacjonuje elementy dwóch przestrzeni wektorowych V i W, przypisując każdy wektor v należący do V jednego wektora W który należy do W, poprzez określoną operację.

Ta transformacja spełnia dwa warunki:

Rysunek 1. Transformacja liniowa dotyczy wektora przestrzeni wektorowej V, aby uzyskać inny wektor należący do przestrzeni wektorowej W. Źródło: f. Zapata.

-Warunek 1

Odnosi się do dodania, tak aby transformacja t -linearna musiała się spełnić, że:

T (v + W) = T (v) + T (W)

-Warunek 2

Drugi warunek reprezentuje jednorodność w rozmnażaniu skalaru przez wektor:

T (cv) = C⋅T (v)

Transformacja liniowa, jak sama nazwa wskazuje, jest odpowiedzialna za mapowanie lub przekształcenie elementów V w elementy W.

Notacja funkcji jest również używana w przypadku transformacji liniowych, a zatem domenę V jest zbiorem elementów (wektorów), które mają być przekształcone, podczas gdy kodominium lub trasa jest wynikowym zestawem.

Przykładem transformacji liniowej jest:

Wskazać, że litera T zostanie użyta. Transformacja zostanie zastosowana do wektora v których składnikami są x i y, które były reprezentowane przez matrycę jednorazową. Rezultatem jest inny wektor W którego składniki są x i 0, reprezentowane również przez matrycę kolumnową.

Dlatego jest to transformacja przestrzeni wektorowej r r² W kierunku przestrzeni wektorowej r², że podsumowując, jest tak napisane:

T: r² → R²         

Jeśli mamy wektor:

Transformacja nas zwraca:

I tak z dowolnym wektorem R². W przykładzie 1 zostanie zweryfikowane, że ta transformacja jest liniowa.

[TOC]

Właściwości transformacji liniowych

Załóżmy, że liniowa transformacja v w w, w której wektory v I Lub Należą do V, a następnie spełnione są następujące właściwości:

Właściwość 1

T (0) = 0

Gdzie 0 jest wektorem zerowym.

Właściwość 2

T (-v) = - t (v)

Właściwość 3

T (Lub  - v) = T (Lub) - T (v)

Właściwość 4

Być v = c₁v₁ + C₂v₂ +.. . +  C_Nv_N

 Więc:

T (c₁v₁ + C₂v₂ +.. . +  C_Nv_N) = c₁ T (v₁) + c₂ T (v₂) +.. . +  C_N T (v_N)

Elementy transformacji liniowej

Niech V i W już wspomniane przestrzenie wektorowe, w których transformacja liniowa T przekształca elementy V do W. Możemy zdefiniować następujące elementy:

-Nucile lub jądro: Jest to podzbiór domeny, do której jest oznaczona przez N (t) albo Ker (t) i zrozum wszystkie elementy V takie, że:

T (v) = 0.

Transformacja liniowa t (v) = 0 jest nazywany transformacja zerowa.

Naturalnie wektor zerowy v = 0 W każdym razie spełnia się z tym warunkiem, ale jądro składa się z całego wektorów innych niż wektory, które również je spełniają, dla danego t.

Może ci służyć: Funkcja rosnąca: jak to zidentyfikować, przykłady, ćwiczenia

-Obraz t: Jest to zestaw wektorów należących do w tak, że są obrazem co najmniej pewnego wektora w v. Jest oznaczony jako Im t) I jest to podzbiór przestrzeni wektorowej W.

Te elementy pomogą nam sklasyfikować przemiany liniowe później.

Czego są transformacje liniowe?

Początkowo transformacje liniowe działają z przestrzeniami wektorowymi, utworzonymi przez wektory. Wiele razy kojarzymy wektory z siłą i innymi wielkościami fizycznymi, jednak w cyfrowym przetwarzaniu obrazu piksel może być reprezentowany przez wektor.

W takim przypadku obraz może być manipulowany przez wygodne transformacje liniowe, aby uzyskać pożądane efekty, na przykład rzutowanie, obracanie, znajdowanie obrazu lustrzanego lub modyfikując jego rozmiar bez zmiany względnych wymiarów.

Transformacje liniowe są również szeroko stosowane w ekonomii i podejmowaniu decyzji, na przykład w celu poznania ilości surowca wymaganego do wyprodukowania określonej partii produktu.

Liczba elementów niezbędnych do złożenia różnych modeli wytwarzanych przez fabrykę, może być wykonywana przez układ matrycy, jak zobaczymy później.

Rodzaje transformacji liniowych (klasyfikacja)

Podobnie jak funkcje, transformacje liniowe mogą być:

-Wstrzykiwanie lub monomorfizmy

-Bijectives lub Epimorfizmy

-Zadoważający lub Izomorfizmy

Ponadto są następujące typy:

-Endomorfizmy

-Automorfizmy.

Trzeby liniowe do iniekcji

Niech przestrzenie V i W wektorowe i t a transformacja liniowa t: v → w. T jest wstrzykiwane, kiedy:

Ker (T) = 0

Liniowe przemiany zatrzymywania

Jeśli V i W są przestrzeniami wektorowymi takimi, że t: v → w, mówi się, że t jest biorcjami, gdy:

Im (t) = w

Bijkłowne transformacje liniowe

Transformacja liniowa T: V → W jest biorcjona, gdy jest zarówno iniekcyjna, jak i zatwierdzająca. Dlatego spełnia się, że:

Ker (T) = 0 I Im (t) = w

Endomorfizmy

Są to liniowe transformacje, w których domena i kodominium się pokrywają.

Automorfizmy

Tego rodzaju transformacje liniowe to biustonomiczne endomorfizmy.

Specjalne transformacje liniowe

Operator liniowy

Transformacja liniowa T: V → V, która przechodzi z przestrzeni wektorowej do tej samej przestrzeni wektorowej Operator liniowy.

Zerowa transformacja

Wspomniany powyżej, zerowa transformacja jest ważna, aby znaleźć jądro transformacji liniowej:

Może ci służyć: tetradecágon

T: v → w taki jak t (v) = 0 Dla każdego v.

Transformacja tożsamości

T: v → v taki, że t (v) = v  Dla każdego v.

Transformacja zdefiniowana przez matrycę

T: v → w taki jak t (v) = Av, gdzie A jest matrycą i v Jest to wektor kolumny.

Funtowanie liniowe

Funkcje liniowe typu y = mx to transformacje liniowe. Weźmy na przykład y = 3x i sprawdź, czy spełnia dwa warunki początku, testując dwie wartości a i b dowolne:

f (a+b) = 3 (a+b) = 3a+3b = f (a)+f (b)

f (ka) = 3 (ka) = k⋅ (3a) = k⋅f (a)

Rzeczywiście jest to transformacja liniowa.

Aplikacje

Transformacje liniowe mają zastosowania matematyczne, takie jak:

-Rotacja osi współrzędnych.

-W rozwiązaniu układów liniowych równań różniczkowych.

-Problemy z własną wartością i automatyczną.

Mają także zastosowania w innych dziedzinach nauki, na przykład w mechanice, mechanice kwantowej i ekonomii, między innymi.

Przykłady transformacji liniowych

Przykład 1

W wielu problemach mechanicznych musimy znaleźć projekcję wektora v należący do kosmosu, na określonej płaszczyźnie. Ten wektor v może na przykład reprezentować siłę.

Załóżmy, że chcesz rzutować wektor v = Na płaszczyźnie XY. Możemy zdefiniować transformację liniową podaną przez następującą matrycę:

Kiedy zastosujemy go do wektora v Otrzymujemy wektor, którego komponent Z jest anulowany. Geometrycznie jest reprezentowany, z rzutem v Na płaszczyźnie xy jako czerwony wektor z dwoma komponentami.

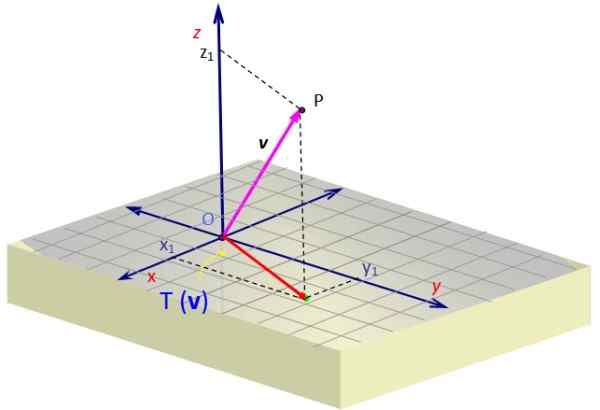Rysunek 2. Projekcja wektora w przestrzeni na płaszczyźnie, która jest uzyskiwana przez transformację liniową. Źródło: f. Zapata.

Przykład 2

Załóżmy, że masz fabrykę, która produkuje trzy rodzaje wózków z zabawkami: C1, C2 i C3, dla których z kolei potrzebujesz trzech rodzajów elementów w niektórych ilościach do produkcji każdego rodzaju wózka:

-Osie lub kawałek

-Koła lub kawałek b

-Podwozie lub kawałek c

Dla każdego rodzaju wózka liczba elementów jest inna, ponieważ modele są różne. Możemy pomieścić ilości w matrycy 3 × 3, w której kolumny są kierowane przez rodzaj wózka, a szeregi odpowiadają ilości elementów niezbędnych do skomplikowania każdego modelu.

Jest to przykład transformacji podanej przez matrycę, która byłaby taka:

Jeśli fabryka otrzyma określone zamówienie, które składa się z X Ilość C1, I  C2 i z Z C3, ile elementów A, B i C musi mieć dostępne do złożenia wózków zamówień?

Może ci służyć: jakie są wyrażenia algebraiczne, a które są najczęstsze?

Musimy znaleźć transformację liniową t (x) tak, aby:

Aby uzyskać wektor i:

To da nam ilość części, które musimy mieć w dyspozycji. W roku rozwiązanym 2 oceniamy skuteczność transformacji liniowych, aby znaleźć ilość części niezbędnych do spełnienia określonego zamówienia.

Rozwiązane ćwiczenia

- Ćwiczenie 1

Sprawdź, czy następująca transformacja t: r² → R² To jest liniowe:

Rozwiązanie

Aby to zrobić, musisz upewnić się, że transformacja spełnia dwa warunki opisane na początku, najpierw dodanie, a następnie iloczyn skalarny dla wektora. Więc musisz wziąć dwa wektory v I  Lub należący do r², Pisanie ich według notacji Matrix lub określenie komponentów.

Te wektory to:

v = x₁, I₁

Lub = x₂, I₂

Pierwszy warunek

-Pamiętając, że wektory są dodawane komponent komponentu, należy zweryfikować, że:

T (v+Lub) = T (v) + T (Lub)

T (v+Lub) = T (x₁+ X₂ ; I₁ + I₂)

Stąd uzyskuje się, że:

T (x₁+ X₂ ; I₁ + I₂) = (x₁+ X₂; 0)

-Z drugiej strony, przy zastosowaniu transformacji do każdego wektora osobno:

T (x₁,I₁) + T (x₂,I₂) = (x₁,0) + (x₂,0)

Dodając powstałe wektory, jest to skutecznie uzyskiwane:

W = (X₁+ X₂; 0)

Ponieważ oba wyniki są identyczne, pierwszy warunek jest spełniony.

Drugi warunek

Teraz zweryfikujemy to poprzez pomnożenie przez twardzinę C, może wyjść z transformacji:

T (cv) = C⋅T (v)

Sean:

v = x₁, I₁

C.v = C⋅x₁, C⋅Y₁

Więc:

T (cv) = T (c⋅x₁, C⋅Y₁ ) = (C⋅x₁ , 0)

Ale wiemy o tym z poprzedniego kroku T (v) = T (x₁, I₁ ) = (X₁ , 0).

Tak więc, ponieważ oba wyrażenia są identyczne, drugi warunek jest również spełniony, a transformacja jest liniowa.

- Ćwiczenie 2

Fabryka wózków z zabawkami składa trzy modele pojazdów: C1, C2 i C3, dla których potrzebujesz kawałków A, B i C, które są odpowiednio osiami, kółkami i podwoziami. Wymagane kwoty znajdują się w poniższej tabeli:

Fabryka została poproszona o przygotowanie 12 modeli C1, 22 C2 i 16 C3. Ile elementów A, B i C jest zobowiązanych do złożenia zamówienia?

Rozwiązanie

Zastosowana jest transformacja liniowa t (x) = y, której wynik jest produktem między matrycami:

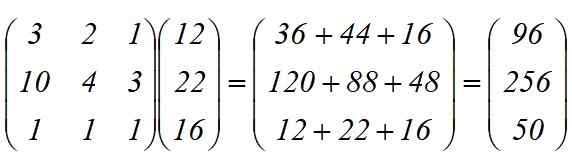
Są one wymagane w sumie:

-96 osi

-256 kół

-50 podwoziów.

Bibliografia

1. Algebra i geometria analityczna. Rdzeń i obraz. Klasyfikacja transformacji liniowych. Odzyskane z: Aga.FRBA.Utn.Edu.ar.
2. Grossman, s. 2012. Algebra liniowa. 7th. Wydanie. McGraw Hill.
3. Gutiérrez, e. 2014. Algebra liniowa i jej aplikacje. Grupa redakcyjna Patria.
4. Larson, r. 2016. Podstawy algebry liniowej. 6th. Wydanie. Cengage Learning.
5. Wikipedia. Aplikacje liniowe. Odzyskane z: jest.Wikipedia.org.