Praca mechaniczna, co jest, warunki, przykłady, ćwiczenia

On Praca mechaniczna Jest zdefiniowany jako zmiana stanu energetycznego systemu, spowodowanego działaniem sił zewnętrznych, takich jak grawitacja lub tarcie. Mechaniczne jednostki pracy w międzynarodowym systemie (SI) to Newton X Metro lub Joules, skrócone przez J.

Matematycznie jest to zdefiniowane jako iloczyn skalarny siły siły przez przemieszczenie wektora. Tak F To jest stała siła i L Jest to przemieszczenie, oba wektory, praca W jest wyrażona jako: W = F ● L

Rysunek 1. Podczas gdy sportowiec podnosi wagę, działa przeciwko grawitacji, ale kiedy utrzymuje wagę bez ruchu, z punktu widzenia fizyki nie wykonuje pracy. Źródło: Needpix.com

Gdy siła nie jest stała, musimy przeanalizować pracę wykonaną, gdy przemieszczenia są bardzo małe lub różnicowe. W takim przypadku, jeśli jest to uważane za punkt wyjścia do punktu A i jako przybycie na B, całkowita praca jest uzyskiwana przez dodanie wszystkich wkładów do tego samego. Jest to równoważne obliczanie następującej całki:

I jak wspomniano na początku, pod warunkiem, że nastąpi zmiana energii systemowej, będzie tak, ponieważ działają na nią siły z zagranicy, dlatego:

Zmienność energii systemowej = praca wykonana przez siły zewnętrzne

ΔE = w_ext

Gdy energia jest dodawana do systemu, w> 0 i po odjęciu<0. Ahora bien, si ΔE = 0, puede significar que:

-Układ jest izolowany i nie działa na niego żadne siły zewnętrzne.

-Istnieją siły zewnętrzne, ale nie pracują nad systemem.

Ponieważ zmienność energii jest równoważna pracy wykonanej przez siły zewnętrzne, jednostką, jeśli energia jest również Joule. Obejmuje to dowolny rodzaj energii: kinetyczny, potencjał, termiczny, chemiczny i więcej.

[TOC]

Warunki, aby były prace mechaniczne

Widzieliśmy już, że praca jest zdefiniowana jako produkt skalarny. Weźmy definicję pracy wykonanej przez stałą siłę i zastosuj pojęcie produktu skalarnego między dwoma wektorami:

W = F ● L = F.L.cos θ

Gdzie F Jest to wielkość siły, L Jest to wielkość przemieszczenia i θ Jest to kąt między siłą a przesunięciem. Na rycinie 2 istnieje przykład nachylonej siły zewnętrznej działającej na blok (system), który wytwarza poziome przemieszczenie.

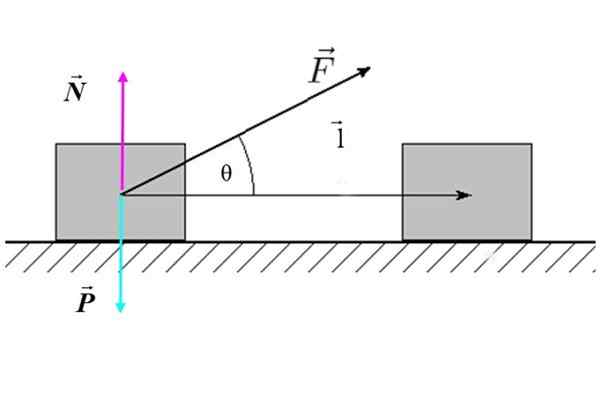Rysunek 2. Schemat wolnego ciała bloku, który porusza się po płaskiej powierzchni. Źródło: f. Zapata.

Przepisywanie pracy w następujący sposób:

W = (f. cos θ). L

Możemy potwierdzić, że tylko składnik siły równolegle do przesunięcia: F. cos θ ejest zdolny do pracy. Jeśli θ = 90º, to cos θ = 0, a praca byłaby nieważna.

Dlatego stwierdzono, że siły prostopadłe do przemieszczenia nie wykonują pracy mechanicznej.

W przypadku ryc. 2, ani normalnej siły N ani waga P Działają, ponieważ oba są prostopadłe do przemieszczenia L.

Oznaki pracy

Jak wyjaśniono powyżej, W Może być pozytywny lub negatywny. Kiedy cos θ> 0, Praca wykonana przez siłę jest pozytywna, ponieważ ma ten sam kierunek ruchu.

Może ci służyć: numer masowy: co to jest i jak go zdobyć (z przykładami)

Tak cos θ = 1, siła i przemieszczenie są równoległe, a praca jest maksymalna.

W przypadku cos θ < 1, la fuerza no está a favor del movimiento y el trabajo es negativo.

Gdy cos θ = -1, Siła jest całkowicie przeciwna do przemieszczenia, na przykład tarcie kinetyczne, którego efektem jest powstrzymanie obiektu, na którym działa. Więc praca jest minimalna.

Zgadza się to z tym, co zostało powiedziane na początku: jeśli praca jest pozytywna, energia jest dodawana do systemu, a jeśli jest ujemna, jest odejmowana.

Sieć W_internet Jest zdefiniowany jako suma prac wykonanych przez wszystkie siły działające w systemie:

W_internet = ∑w_Siema

Następnie możemy stwierdzić, że aby zagwarantować istnienie pracy mechanicznej netto, konieczne jest:

-Siły zewnętrzne działają na obiekcie.

-Siły te nie są prostopadłe do przemieszczenia (cos θ ≠ 0).

-Prace wykonane przez każdą siłę nie są ze sobą anulowane.

-Jest przemieszczenie.

Przykłady pracy mechanicznej

-Ilekroć konieczne jest umieszczenie obiektu w oparciu o odpoczynek, konieczne jest wykonywanie pracy mechanicznej. Na przykład popchnij lodówkę lub ciężki bagażnik na poziomej powierzchni.

-Innym przykładem sytuacji, w której konieczne jest wykonanie pracy mechanicznej, jest zmiana prędkości poruszającej się piłki.

-Konieczne jest wykonanie pracy, aby podnieść obiekt na określonej wysokości na podłodze.

Teraz istnieją równie powszechne sytuacje NIE Prace są wykonywane, chociaż pozory wskazują inaczej. Powiedzieliśmy, że aby podnieść obiekt na określonej wysokości, musimy wykonywać pracę, więc ładujemy obiekt, podnosimy go nad głową i trzymamy tam. Czy pracujemy?

Najwyraźniej tak, ponieważ jeśli przedmiot jest ciężki, ramiona wkrótce się zmęczy, jednak bez względu na to, ile pracy jest wykonywane, praca nie jest wykonywana z punktu widzenia fizyki. Dlaczego nie? Ponieważ obiekt się nie porusza.

Innym przypadkiem, w którym pomimo siły zewnętrznej, nie wykonuje pracy mechanicznej, jest to, że cząstka ma jednolity ruch kołowy.

Może ci służyć: normalny wysiłek: z czego składa się, jak jest obliczane, przykłady

Na przykład dziecko, które zwraca kamień przywiązany do sznurka. Napięcie sznurka to siła dośrodkowa, która umożliwia obrót kamienia. Ale przez cały czas siła ta jest prostopadła do przemieszczenia. Zatem nie wykonuj pracy mechanicznej, mimo że faworyzuje ruch.

Twierdzenie o energii pracy

Energia kinetyczna systemu jest tym, co ma pod jego ruchem. Tak M jest ciasto i v Jest to prędkość ruchu, energia kinetyczna jest oznaczona przez K I jest podany przez:

K = ½ mV²

Z definicji energia kinetyczna obiektu nie może być ujemna, ponieważ zarówno masa, jak i kwadrat prędkości są zawsze ilościami dodatnimi. Energia kinetyczna może wynosić 0, gdy obiekt jest w spoczynku.

Aby zmienić energię kinetyczną systemu, konieczne jest-. W tym celu należy zatem wykonywać pracę netto w systemie:

W_internet = ΔK

To jest twierdzenie o pracy - energia kinetyczna. Stwierdza, że:

Praca netto jest równoważna zmianie energii kinetycznej systemu

Zauważ, że chociaż K jest zawsze pozytywne, KK może być dodatnie lub ujemne, ponieważ:

ΔK = k_finał - K _wstępny

Tak K_finał >K _wstępny System zyskał energię i Δk> 0. Wręcz przeciwnie, tak K_finał < K _wstępny, System przyniósł energię.

Praca wykonana w celu rozciągnięcia sprężyny

Podczas rozciągania (lub kompresji) sprężyny konieczne jest wykonanie pracy. Ta praca jest przechowywana wiosną, pozwalając z kolei wykonywać pracę, powiedzmy, blok przymocowany do jednego z jego końca.

Prawo Hooke stwierdza, że ​​siła wywierana przez wiosnę jest siłą zwrotną - jest sprzeczne z przesiedleniem - a także proporcjonalnym do wspomnianego wysiedlenia. Stała proporcjonalności zależy od tego, jak sprężyna jest: miękka i łatwo odkształcalna lub sztywna.

Ta siła jest podana przez:

F_R = -kx

W wyrażeniu, F_R To jest siła, k To jest stała sprężyna i X To jest przemieszczenie. Znak ujemny wskazuje, że siła wywierana przez sprężynę sprzeciwia się przemieszczeniu.

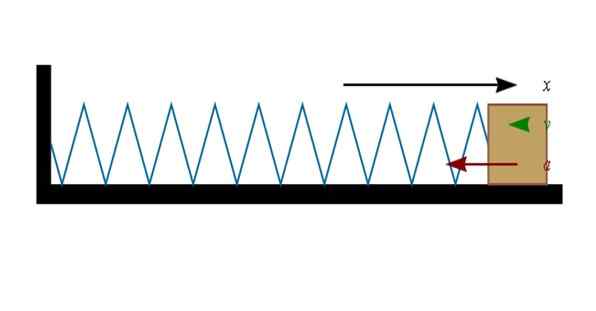Rysunek 3. Sprężona lub rozciągnięta sprężyna działa na obiekcie przywiązanym do jego końca. Źródło: Wikimedia Commons.

Jeśli sprężyna zostanie skompresowana (po lewej stronie na rysunku), blok na jego końcu przesunie się w prawo. A kiedy sprężyna jest rozciągnięta (po prawej), blok będzie chciał przesunąć się w lewo.

Aby skompresować lub rozciągnąć sprężynę, jakiś agent zewnętrzny musi wykonać zadanie, a ponieważ jest to zmienna siła, aby obliczyć tę pracę, musisz użyć definicji, która wystąpiła na początku:

Może ci służyć: Darcy Law

Bardzo ważne jest, aby zauważyć, że jest to praca wykonana przez agenta zewnętrznego (na przykład ręka osoby) w celu kompresji lub rozciągnięcia sprężyny. Dlatego znak negatywny nie pojawia się. A ponieważ pozycje są kwadratowe, bez względu na to, czy są to uciśnięcia lub wydłużenia.

Praca, która z kolei wykona sprężynę na bloku, to:

W_wiosna = -W_ext

Ćwiczenia

Ćwiczenie 1

Blok na rycinie 4 ma masę m = 2 kg i przesuwa się po pochyłej płaszczyźnie bez tarcia, z α = 36.9. Zakładając, że wolno zejść z reszty z górnej części płaszczyzny, której wysokość wynosi h = 3 m, znajdź prędkość, z jaką blok dociera do podstawy płaszczyzny, poprzez kinetykę twierdzenia o energii roboczej.

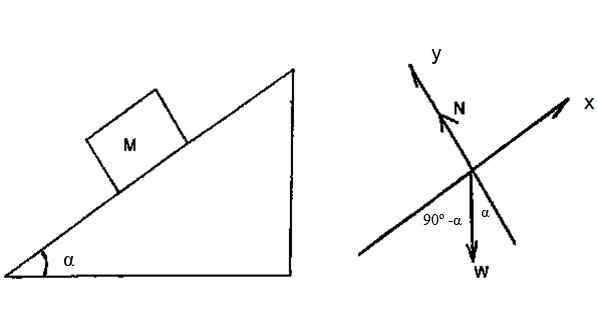Rysunek 4. Blok zsuwa się po nachylonej płaszczyźnie bez pocierania. Źródło: f. Zapata.

Rozwiązanie

Schemat wolnego ciała pokazuje, że jedyną siłą zdolną do pracy na bloku jest waga. Dokładniej: składnik wagi wzdłuż osi x.

Odległość przebywająca przez blok w płaszczyźnie jest obliczany za pomocą trygonometrii:

D = 3 / (cos 36.9º) M = 3.75 m

W_waga = (Mg). D. cos (90 α) = 2 x 9.8 x 3.75 x cos 53.1st J = 44.1 J

Pracując kinetyką twierdzenia o energii:

W_internet = ΔK

W_internet = W_waga

ΔK = ½ mV_F²- ½ mV_albo²

Ponieważ jest zwolniony z odpoczynku, v_albo = 0, W związku z tym:

W_internet = ½ mV_F²

Ćwiczenie 2

Pozioma sprężyna, której stał. Jedna osoba ściska drugi koniec w odległości 5 cm. Oblicz: a) siła wywierana przez osobę, b) praca, którą wykonał, aby skompresować sprężynę.

Rozwiązanie

a) Wielkość siły przyłożonej przez osobę jest:

F = kx = 750 N/ m . 5 x 10 ^-2 M = 37.5 n.

b) Jeśli koniec sprężyny jest pierwotnie w x₁ = 0, aby przenieść go stamtąd do ostatecznej pozycji x₂ = 5 cm, należy wykonać następujące prace, zgodnie z wynikiem uzyskanym w poprzednim rozdziale:

W_ext = ½ k (x₂² - X₁²) = 0.5 x 750 x (0.05² -0²) J = 0.9375 J.

Bibliografia

1. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Głośność 2. Dynamiczny. Pod redakcją Douglas Figueroa (USB).
2. Iparguirre, l. 2009. Podstawowa mechanika. Kolekcja nauk przyrodniczych i matematyka. Bezpłatna dystrybucja online.
3. Knight, r. 2017. Fizyka dla naukowców i inżynierii: podejście strategiczne. osoba.
4. Fizyka librettexts. Twierdzenie o energii pracy. Odzyskane z: Phys.Librettexts.org
5. Praca i energia. Odzyskane z: fizyka.Bu.Edu
6. Praca, energia i moc. Odzyskane z: NCERT.Nic.W