Poziome funkcje strzelania, formuły i równania, ćwiczenia

On Strzelanie poziome Jest to uruchomienie pocisku o poziomej prędkości z pewnej wysokości i pozostawione do działania grawitacji. Bez uwzględnienia oporu powietrza, trajektoria opisana przez telefon komórkowy będzie miała kształt łuku paraboli.

Rzutowanie obiektów poziomo jest dość powszechne. Pociski są wyrzucane z wszelkiego rodzaju końcami: od kamieni, z którymi tamy były przygnębione na początku historii, po te, które są przeprowadzane w sporcie piłki i są ściśle za nim tłumy.

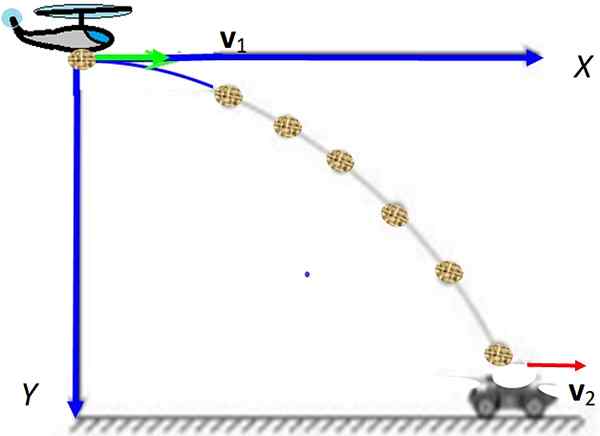
Rysunek 1. Strzelanie poziome z czerwonymi komponentami prędkości. Zauważ, że składnik poziomy pozostaje stały, a pionowy rośnie. Źródło: Wikimedia Commons.

[TOC]

Charakterystyka

Główne cechy strzelania poziomego to:

-Początkowa prędkość dostarczona do pocisku jest prostopadła do grawitacji.

-Ruch odbywa się w płaszczyźnie, więc potrzebne są dwa współrzędne: X I I.

-Odbywa się to z pewnej wysokości H nad poziomem gruntu.

-Czas, w którym pocisk trwa w powietrzu czas lotu.

-Czynniki takie jak odporność na powietrze lub fluktuacje nie są brane pod uwagę pod względem wartości G.

-Kształt, rozmiar i masa pocisku nie wpływają na jego ruch.

-Ruch rozkłada się na dwa jednoczesne ruchy: jeden pionowy w dół pod działaniem G; Drugi, pozioma, ze stałą prędkością.

Wzory i równania

Równania kinowe dotyczące uruchomienia poziomego są uzyskiwane z równań dla wolnego upadku i równania równomiernego ruchu prostoliniowego.

Może ci służyć: energia wewnętrzna

Jak wyraźnie pokazuje animacja na rycinie 1, pocisk jest wyposażony w poziomą prędkość początkową, oznaczoną jako v_albo = v_wół Siema (Bold w drukowanym tekście wskazuje, że jest to wektor).

Należy zauważyć, że początkowa prędkość ma wielkość v_wół i jest skierowany wzdłuż osi X, Jaki jest kierunek wektora jednostki Siema. W animacji ostrzega się również, że prędkość początkowa nie ma składnika pionowego, ale w miarę upadku komponent ten rośnie jednolicie dzięki działaniu G, Przyspieszenie grawitacyjne.

Jeśli chodzi o poziomy składnik prędkości, pozostaje on stały, podczas gdy ruch trwa.

Zgodnie z tym, co zostało powiedziane, pozycje są ustalane jako funkcja czasu, zarówno na osi poziomej, jak i w osi pionowej. Prawo jest przyjmowane jako osi +x, a w dół jest adres -i. Wartość grawitacji to G = -9.8 m/s² albo -32 stóp/s²:

x (t) = x_albo + v_wół.t (pozycja pozioma); v_wół To jest stałe

i (t) = y_albo + v_Oy.T - ½ g.T² (pozycja pionowa); v_I = v_Oy - G.T (prędkość pionowa)

Pozycja, prędkość, czas lotu i maksymalny zasięg poziomego

Równania są uproszczone, jeśli wybiorą następujące początkowe pozycje: X_albo = 0, I_albo = 0 w miejscu uruchomienia. Oprócz v_Oy = 0, Ponieważ telefon komórkowy jest rzutowany poziomo. Z tym wyborem równania ruchu są takie:

x (t) = v_wół.T; v_X = v_wół

i (t) = - ½ g.T²; v_I = - g.T

Gdy czas nie jest dostępny, równanie odnoszące prędkości i przemieszczenia jest przydatne. Jest to ważne dla prędkości pionowej, ponieważ poziome pozostaje stałe w całym ruchu:

Może ci służyć: fluor wapnia (CAF2): struktura, właściwości, zastosowania

v_I² = v_Oy² + 2.G .y = 2.G.I

Czas lotu

Aby obliczyć Czas lotu t_lot, Załóżmy, że telefon komórkowy jest rzutowany z wysokości H na podłodze. Ponieważ pochodzenie systemu odniesienia w punkcie uruchomienia zostało wybrane, gdy dotrze do ziemi, jest w pozycji -H. Zastąpienie tego w równaniu 2) otrzymuje się:

-H = - ½ g.T²_lot

T_lot = (2H/g)^½

Maksymalny zakres

On Poziomy zasięg Tym razem uzyskuje się przez zastąpienie X (t):

X_Max = v_wół. (2H/g)^½

Rozwiązane ćwiczenia

-Ćwiczenie rozwiązane 1

Helikopter leci poziomo, utrzymując stałe wysokość 580 m, gdy uwalnia pudełko zawierające jedzenie na obozie dla uchodźców. Pudełko wyląduje w poziomej odległości 150 m od momentu jego wystrzelenia. Znajdź: a) czas lotu pudełka.

b) szybkość helikoptera.

c) Jak szybko dotknęło pudełko?

Rozwiązanie

a) Wysokość h, z której uwalnia się jedzenie, wynosi h = 500 m. Z tymi danymi podczas wymiany otrzymujesz:

T_lot = (2H/g)^½= (2 x 580/9.8) ^½S = 10.9 s

b) Helikopter przenosi poziomą prędkość początkową v_wół pakietu, a ponieważ jeden z danych jest X_Max:

X_Max = v_wół. (2H/g)^½ ® v_wół = x_Max /(2H/g)^½= x_Max / T_lot = 150 m/ 10.9 s = 13.8 m/s

c) prędkość pocisku w dowolnym momencie jest:

v_I = -G.T = -9.8 m/ s² x 10.9 s = -106.82 m/s = - 384.6 km/h

Znak ujemny wskazuje, że telefon komórkowy porusza się w dół.

-Ćwiczenie rozwiązane 2

Z samolotu, który leci poziomo na wysokości H = 500 m I 200 km/h Pakiet padnie, który musi spaść na otwarty pojazd, który maszeruje 18 km/h na drodze. W której pozycji powinien samolot pozwolić, aby paczka spadła do pojazdu? Nie bierz pod uwagę oporu powietrza ani prędkości wiatru.

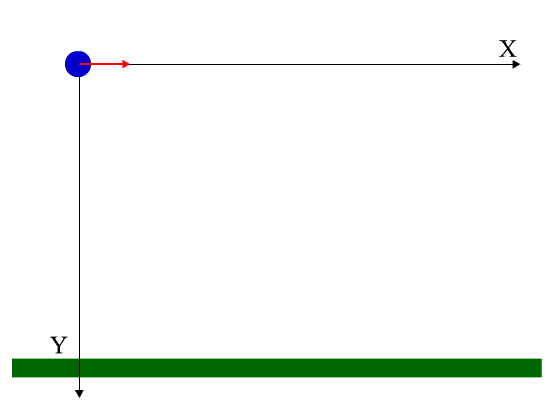
Może ci służyć: analiza wymiarowaRysunek 2. Schemat ćwiczeń rozwiązanych 2. Źródło: Przygotowane przez F. Zapata.

Rozwiązanie

Wygodne jest najpierw przekazanie wszystkich jednostek do systemu międzynarodowego:

18 km/h = 6 m/s

200 km /h = 55 m /s

Istnieją dwa telefony komórkowe: płaszczyzna (1) i pojazd (2) i konieczne jest wybrać układ współrzędnych, aby zlokalizować je oba. Jest to wygodne w punkcie początkowym pakietu w samolocie. Pakiet jest rzutowany poziomo z prędkością, którą nosi samolot: v₁, podczas gdy pojazd przenosi się do v₂ domniemana stała.

-Samolot

Położenie początkowe: x = 0; y = 0

Początkowa prędkość = v₁ (poziomy)

Równania pozycji: i (t) = -½g.T²  ; x (t) = v₁.T

-Pojazd

Położenie początkowe: x = 0, y = -h

Początkowa prędkość = v₂  (stały)

x (t) = x_albo + v₂. T

Czas, w którym trwa lot pakietu, to:

T_lot = (2H/g)^½ = (2 × 500/9.8)^½S = 10.1 s

W tej chwili pakiet doświadczył poziomego przemieszczenia:

X_Max = v_wół . (2H/g)^½= 55 m/s x 10.1 s = 556 m.

W tej chwili pojazd poruszał się również w poziomie:

x (t) = v₁.T = 6 m/s x10.1 s = 60.6 m

Jeśli samolot natychmiast zwolni paczkę, że pojazd przejdzie pod nim, nie będzie w stanie wpaść w nią. Aby to się stało, musi to odrzucić:

D = 556 m - 60.6 m = 495.4 m.

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill. 74-84.
2. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 1. Kinematyka. Pod redakcją Douglas Figueroa (USB).117 - 164.
3. Ruch pocisku. Odzyskane z: Phys.Librettexts.org.
4. Rex, a. 2011. Podstawy fizyki. osoba. 53-58.
5. Tippens, s. 1. 2011. Fizyka: koncepcje i zastosowania. 7. edycja. McGraw Hill. 126-131.