Rodzaje funkcji i ich wykresy

Są zróżnicowane Rodzaje funkcji które są używane do modelowania problemów w gałęziach wiedzy, takich jak nauki przyrodnicze, administracja, gospodarka i nauki społeczne. Matematycznie, funkcją jest związek między dwiema lub więcej zmiennymi.

Wiele razy niektóre obiekty lub ilości są ze sobą powiązane. Kwoty te są reprezentowane przez zmienne. Na przykład istnieją dwie powiązane zmienne, należące do dwóch zestawów A i B, niekoniecznie numeryczne, chociaż przez większość czasu są-.

Aby uznać się za funkcję, związek ten musi spełniać dwa warunki: pierwsze jest to, że wszystkie elementy początkowego zestawu do uczestnictwa, a drugi, że każdy element wspomnianego zestawu jest związany tylko z jednym z elementów zestawu B.

Zmienne są zwykle wywoływane z literami X I I, z X jak Zmienna niezależna I I jak zmienna zależna. Oczywiście można je wywołać w dowolny inny sposób, wybierając nazwę zmiennej zgodnie z wielkością, którą reprezentuje.

Związek między nimi jest oznaczony przez list F -lub inna litera alfabetu i jest reprezentowana na kilka sposobów, takich jak zestaw uporządkowanych par, wykres, wyrażenie werbalne lub formuła algebraiczna:

• f (x) = x + 1
• Populacja P pewnego miasta w określonym przedziale czasowym t.
• H (x) = (1,3); (2,4); (3,5); (4.6)

Funkcje charakteryzują się posiadaniem domena I zasięg lub trasa. Domena to zestaw wartości, które zmienna X Możesz wziąć, podczas gdy zakres jest zbiorem wartości, które nabywa funkcję zależną lub zmienną i.

Klasyfikacja funkcji

Funkcje można pogrupować w 5 dużych kategorii, jak odzwierciedlono w następującym schemacie, w którym każda grupa jest oznaczona liczbą rzymską i kolorem. Począwszy od lewej do prawej, funkcje są klasyfikowane zgodnie z:

• I) jego forma.
• Ii) Symetria.
• Iii) sposób wyrażenia zmiennej.
• Iv) jego ciągłość i monotonia.
• V) sposób, w jaki elementy domeny są powiązane z elementami zakresu.

Główne kryteria klasyfikacji funkcji. Źródło: f. Zapata.

Teraz postępuj zgodnie z krótkim opisem każdego z rodzajów funkcji z odpowiednimi przykładami.

I) funkcje zgodnie z jego formą

Siema.1) Funkcje algebraiczne

Należą one do najczęściej używanych funkcji w wielu dziedzinach nauki, a zatem są najbardziej znani. Charakteryzują się posiadaniem jako zasady korespondencji, wyrażenia algebraicznego.

Z kolei funkcje algebraiczne są podzielone na następujące typy:

• Siema.1.a) Wielomian lub wielomian.
• Siema.1.b) racjonalne.
• Siema.1.c) irracjonalne.
• Siema.1.d) według sekcji.

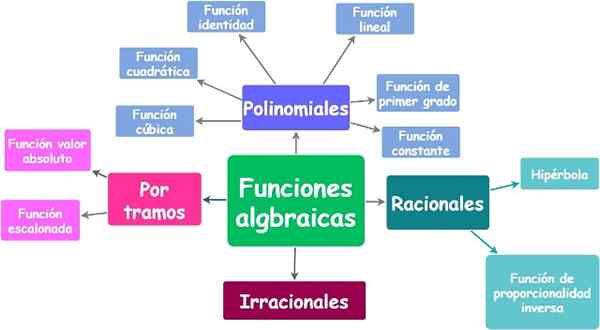Funkcje algebraiczne i ich typy. Źródło: f. Zapata.

Siema.1.A) Funkcje wielomianowe lub wielomianowe

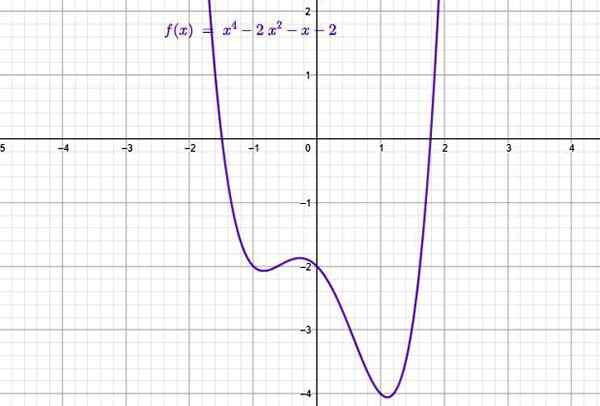Przykład funkcji typu wielomianowego. Źródło: f. Zapata przez Geogebra.

Składają się z sum terminów, których ogólną formą jest:

P (x) = a_NX^N + Do _N-1X^N-1 +… Do₁x + a₀

Gdzie współczynniki_N, Do _N-1… Do₁, Do₀ Są liczbami rzeczywistymi, a N jest liczbą całkowitą. Domena funkcji wielomianowych jest zestaw R liczb rzeczywistych, a także są funkcjami ciągłymi w tej dziedzinie.

Na górnej figurze znajduje się wykres następującej funkcji wielomianowej rzędu 4:

f (x) = x⁴ - 2x² - x -2

Wśród funkcji wielomianowych niektóre szczególne przypadki są rozróżniane, zgodnie z wartościami współczynników. Warto uważnie rozważyć, ponieważ są one bardzo przydatne w wielu sytuacjach:

i) stała funkcja

Istnieje stała funkcja, gdy wszystkie współczynniki są anulowane, z wyjątkiem₀:

f (x) = a₀ = k

Wykres funkcji stałej jest linią prostą równoległą do osi poziomej, takiej jak linie:

• f (x) = 2
• g (x) = π
• H (x) = -3/2

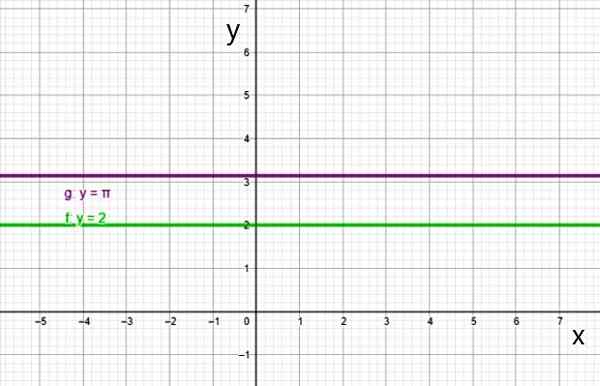Dwa przykłady stałej funkcji. Źródło: f. Zapata.

Ii) Funkcja pierwszego stopnia

Pierwsza funkcja -stope lub powiązana funkcja to, której wykres jest linią prostą. Jest to szczególny przypadek funkcji wielomianowej, w której wszystkie współczynniki pierścienia₁ już₀. Jest podany przez:

f (x) = a₁x + a₀

Wartość a₁ Jest to nachylenie linii, która daje miarę jej skłonności i₀ Jest to cięcie linii z osą pionową. Oba mogą przyjmować wartości dodatnie lub ujemne.

Przykłady funkcji pierwszego stopnia są następujące:

• G (x) = 2x -1
• H (x) = -6x +5/2

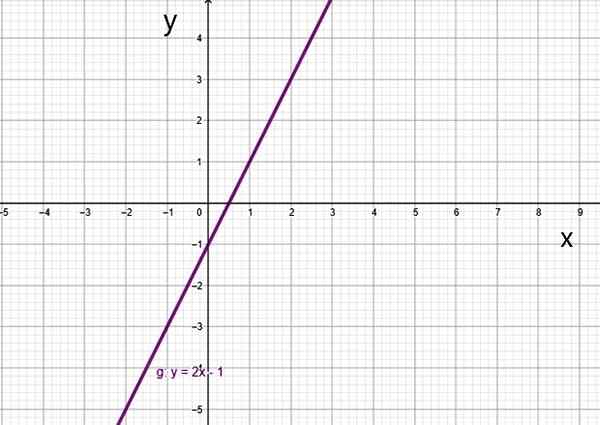Funkcja pierwszego stopnia f (x) = 2x-1. Źródło: f. Zapata.

Istnieje specjalny przypadek, który jest funkcją liniową.

Może ci służyć: środkowe miary tendencji dla zgrupowanych danych: formuły, ćwiczenia

iii) funkcja liniowa

Kiedy współczynnik do₀ Jest 0, funkcja zawsze przechodzi przez pochodzenie i jest wyrażana przez f (x) = a₁X, dzwoniąc Funtowanie liniowe, Jak się masz:

• f (x) = 5x
• G (x) = -7x

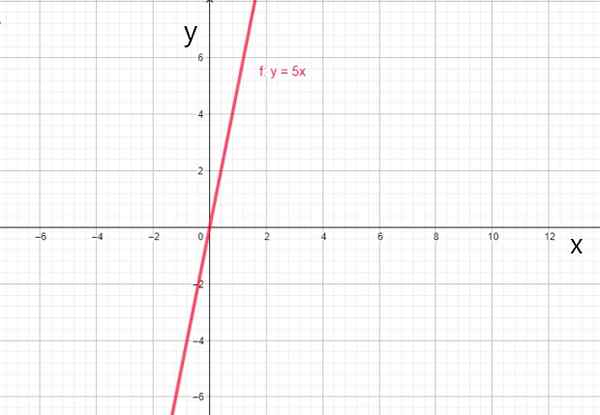Funkcja liniowa f (x) = 5x. Źródło: f. Zapata.

iv) Funkcja tożsamości

Jest to szczególny przypadek funkcji liniowej, w której₁ = 1:

f (x) = x

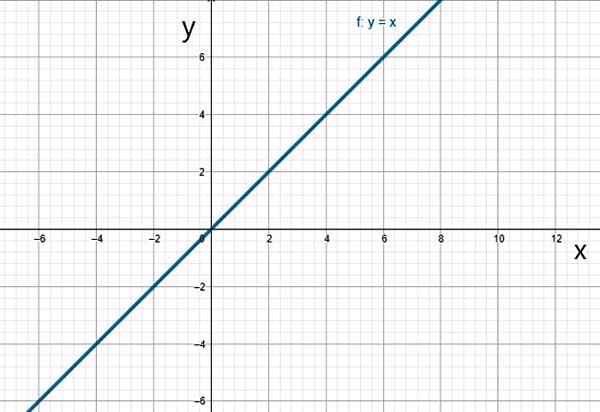Funkcja tożsamości. Źródło: f. Zapata.

v) funkcja kwadratowa

Ma ogólną formę:

f (x) = a₂X² +Do₁x + a₀

Z₂  ≠ 0.

Jego wykres jest przypowieścią, której osi osiowa lub symetria jest równoległa do osi organów. Zawsze przecina oś pionową w punkcie współrzędnej x = 0, y = a₀. Jeśli chodzi o skrzyżowania z osą poziomą, może mieć maksymalnie 2.

Przykłady funkcji kwadratowych są:

• f (x) = x² - 3x - 4
• G (x) = 4x²
• H (x) = x²-1

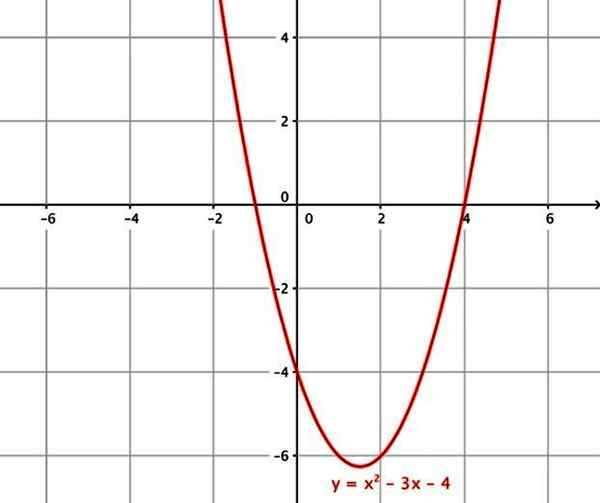Funkcja kwadratowa. Źródło: Wikimedia Commons.

vi) funkcja sześcienna

Jak sama nazwa wskazuje, funkcja sześcienna zawiera moc 3:

f (x) = a₃X³ + Do₂X² + Do₁x + a₀

Współczynnik a₃ Zawsze różni się od 0, jak w tych przypadkach:

• f (x) = x³
• G (x) = 5x³ - 2
• H (x) = -3x³ + 4x² + 10x + 1

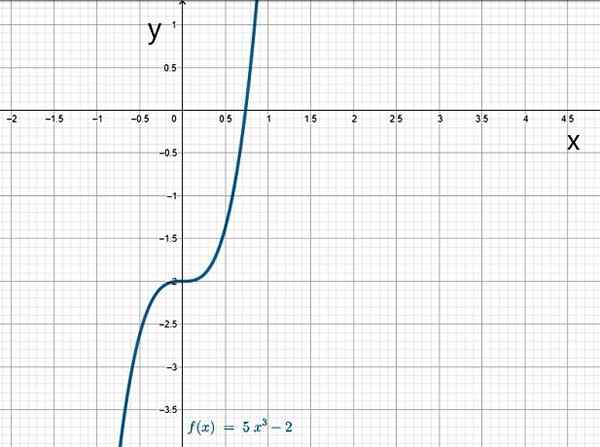Funkcja sześcienna. Źródło: f. Zapata.

Siema.1.b) funkcje racjonalne

Racjonalne funkcje mają formę:

 Gdzie p (x) i q (x) są nieredukowalnymi wielomianami, to znaczy nie mają wspólnego czynnika, a w każdym razie q (x) ≠ 0.

Z domeny funkcji racjonalnych, wszystkie wartości, które pierścienia mianownik q (x), to znaczy jego korzenie, podczas gdy wartości wartości wartości wartości I które określają poziome asymptoty.

Asymptota to linia, do której zbliża się funkcja, zarówno po lewej, jak i po prawej stronie, powyżej lub poniżej, ale nigdy się nie przekracza. Takie linie mogą być pionowe, poziome lub nachylone.

Przykładami funkcji racjonalnych są:

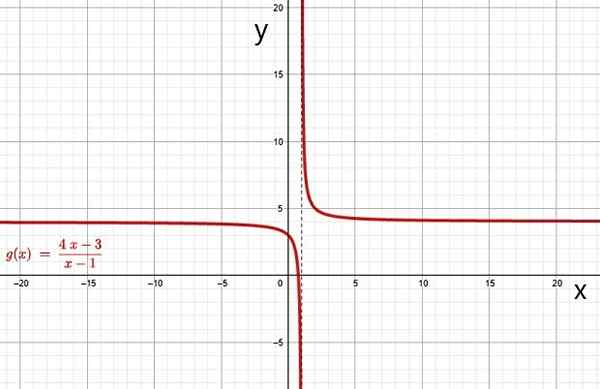Funkcja wymierna. Źródło: f. Zapata przez Geogebra.

i) Hiperbola

Wykres funkcji racjonalnej jest hiperboli, gdy wielomian w mianowniku Q (x) ma stopień 1. Wykres funkcji f (x) i g (x) powyższych przykładów to hiperbole, można go łatwo sprawdzić za pośrednictwem bezpłatnego oprogramowania graficznego online, takiego jak Geogebra.

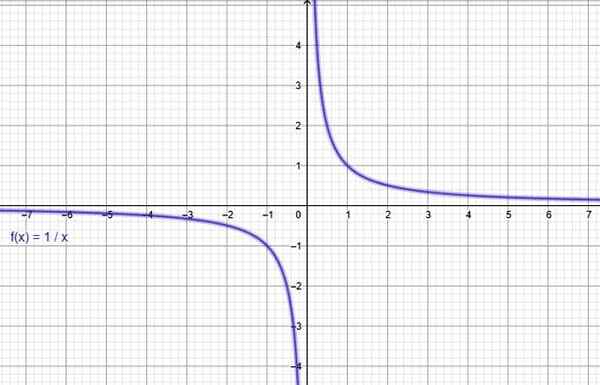Funkcja y = 1/x. Źródło: f. Zapata przez Geogebra.

Ii) Odwrotna funkcja proporcjonalności

Jest to funkcja formy:

Gdzie c jest realnym numerem różnym od 0. Jego domena jest zbiorem liczb rzeczywistych, z wyjątkiem 0.

Siema.1.c) irracjonalne funkcje

To te, których niezależna zmienna jest pod znakiem radykalnym. Jego ogólna forma to:

Niektóre z tych funkcji mogą być:

• 
• 

Domena tych funkcji jest określana w następujący sposób:

-Jeśli korzenie są z wskaźnika momentu obrotowego, kwota subradical f (x) musi zawsze być 0 lub dodatnia.

-Gdy korzenie są dziwne, F (x) może być dodatnie lub ujemne. Dlatego w tym przypadku dziedziną funkcji są liczby rzeczywiste.

Na przykład domena:

Jest to zbiór liczb rzeczywistych, tak że X-3 jest większy lub równy 0. W takim przypadku x musi być większe lub równe 3. Dlatego domeną tej funkcji jest zestaw wartości interwału [3, ∞+).

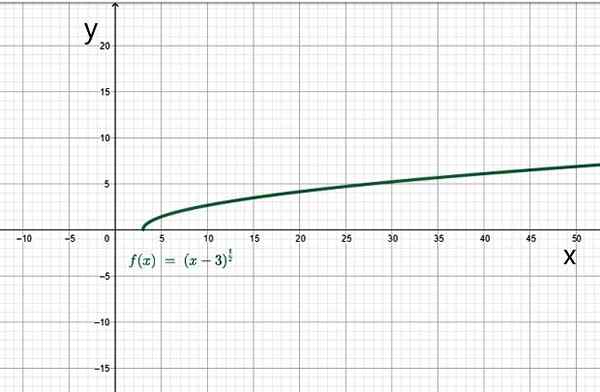 Przykład funkcji irracjonalnej. Źródło: f. Zapata.

Siema.1.d) funkcje na kawałki lub według sekcji

Funkcja w częściach, według sekcji lub elementów, jest taka, która wymaga więcej niż jednej formuły dla różnych wartości domeny. Oto kilka przykładów Twojej aplikacji:

-Stawki za wysyłanie pakietów pocztą, w zależności od masy lub wolumenu, pochodzenia i miejsca docelowego tego samego.

-Stawki za usługi, na przykład telefonię i energię elektryczną.

-Sprzedaż biletów na muzea lub parki rozrywki, w zależności od wieku.

W formie matematycznej funkcja w części może być na przykład:

Domena funkcji w części zależy od jej definicji. W poprzednim przykładzie domena jest zestawem utworzonym przez: (-∞, -1) ∪ [1,+∞).

Funkcja wartości bezwzględnej. Źródło: f. Zapata przez Geogebra.

Ii) Funkcja Escalonada

Wykres tej funkcji według sekcji składa się z kroków, takich jak te z drabiny lub może mieć różne wysokości, w zależności od sposobu zdefiniowania funkcji.

Może ci służyć: Hipparco z Nicea: biografia i wkład w naukę

W tym celu wybrano skończony interwał [a, b], który zawiera pewną skończoną liczbę nieciągłości, zwaną x_Siema < x₁ < x₂ <… . x_N  I wybiera się otwarty interwał (x_Siema , X_I+1) Dać mu stałą wartości s_Siema, Ze skokami w punktach x_Siema. Wartość s_Siema Jest to wysokość danego kroku.

Przykładem funkcji zatoczonej jest cała część, która przyjmuje dowolną liczbę i kojarzy ją z następującą liczbą całkowitą, albo przez nadmiar lub domyślnie. Poniżej znajduje się cała część:

[x] = (większa liczba całkowita ≤ x)

Zgodnie z tą funkcją cała część 2.5 to:

[2.5] = (większa liczba całkowita ≤ 2.5) = 2

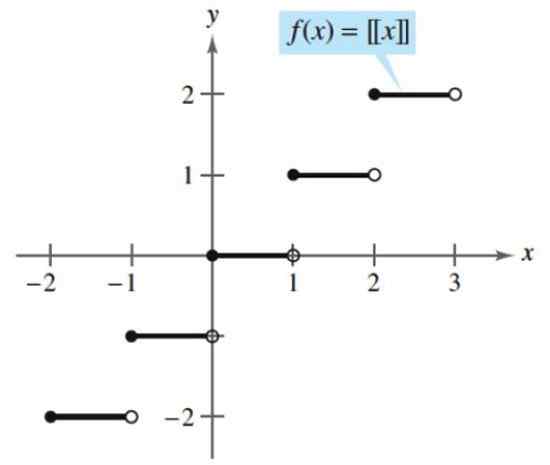Cała część. Źródło: Larson, r. Obliczanie za pomocą geometrii analitycznej. McGraw-Hill.

Siema.2) Funkcje transcendentne

Funkcje niealgebraiczne nazywane są transcendentami. Funkcje wykładnicze, logarytmiczne i trygonometryczne są funkcjami transcendentnymi.

W nich zmienna X Jest to część argumentu funkcji lub jako część wykładnika lub wskaźnik niektórych korzeni, na przykład:

• f (x) = log (x+1)
• H (x) = -0.2⋅8^-3x

Funkcje transcendentne mają wiele zastosowań, na przykład w badaniu wibracji i fal, rozkładów prawdopodobieństwa, modelowaniu fal, wzrostu różnorodnych populacji, rozkładu radioaktywnego, stopach procentowych i wielu innych. 

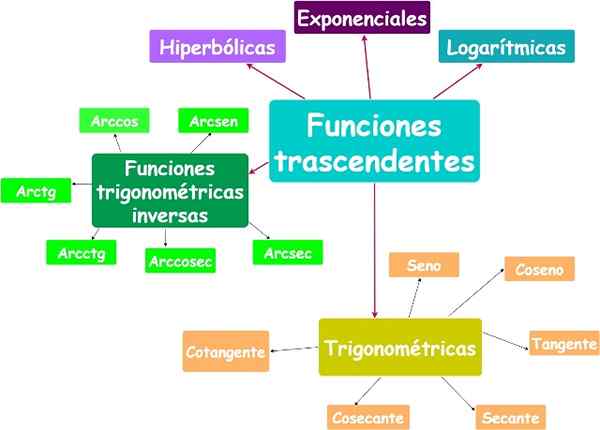Główne funkcje transcendentne. Źródło: f. Zapata.

Siema.2.a) Funkcja wykładnicza 

Funkcja wykładnicza jest zdefiniowana przez:

f (x) = a^X

Gdzie A jest podstawą, która jest zawsze dodatnią liczbą 1, a zmienna, liczba rzeczywista, pojawia się w wykładniku. Ogólnie rzecz biorąc, funkcja wykładnicza jest napisana:

f (x) = a⋅a^Bx

Tutaj a i b są prawdziwymi współczynnikami. Poniżej przedstawiono funkcje tego typu:

• f (x) = 5e^X
• H (x) = 4. 10^5x
• g (t) = 8e^-2t

Baza I, Gdzie I Jest to liczba Euler 2.71828 ..., często pojawia się w problemach nauki i inżynierii, a także statystyk. Gdy funkcja ma tę podstawę, jest wywoływane Naturalna funkcja wykładnicza.

Domena funkcji wykładniczej jest zbiór liczb rzeczywistych, podczas gdy zakres jest liczbami dodatnimi.

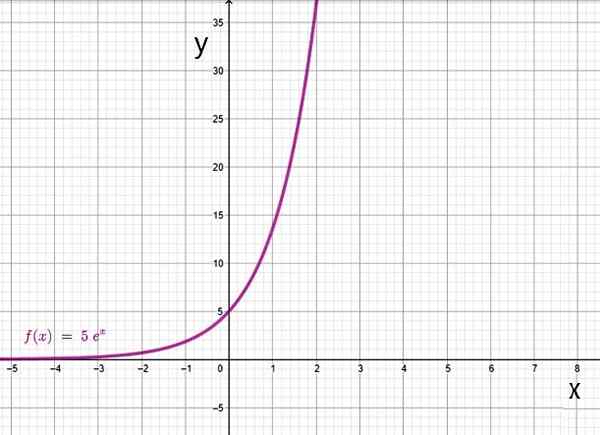Funkcja wykładnicza na podstawie. Źródło: f. Zapata przez Geogebra.

Siema.2.b) Funkcja logarytmu

Ze swojej części funkcja logarytmu na podstawie Do Jest to odwrotna funkcja funkcji wykładniczej na podstawie Do. Tak:

dziennik_Do x = y

Więc:

x = a^I

W szczególności, jeśli podstawą logarytmu jest liczba e, funkcja jest wywoływana Neperiańska funkcja logarytmu I jest to oznaczone jako Ln. Funkcje tego typu to:

• f (x) = ln x
• g (x) = log (x+1)
• H (t) = 1 - log x²

Domena funkcji logarytmu, niezależnie od podstawy, są dodatnie liczby rzeczywiste, nie uwzględniając 0. To znaczy nie ma logarytmów liczb ujemnych ani 0.

Jednak logarytm może być 0 lub ujemny: logarytm liczby między 0 a 1 jest ujemny i ze względu na jej część osiąga_Do 1 = 0.

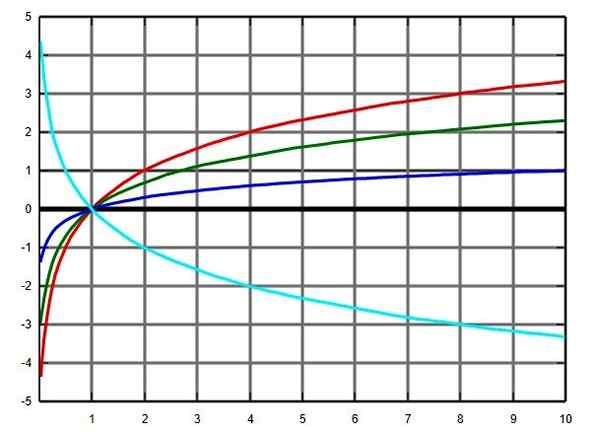Wykres funkcji logarytmu w kilku podstawach: podstawa 2 w kolorze czerwonym, zielonym E, baza niebieska i turkus na podstawie 0.5. Źródło: Wikimedia Commons.

Siema.2.c) funkcje trygonometryczne

Są to te, które pochodzą z powodów trygonometrycznych: zatok, cosinus, styczna, suszenie, harmonowanie i kąt. Są one oznaczone odpowiednio jako:

Sen X, cos x, tg x, sec x, harm x i cotg x

Są to funkcje okresowe, co oznacza, że ​​jego forma jest powtarzalna, więc są one bardzo przydatne do opisania naturalnych zjawisk, takich jak sygnały, oscylacje, ruch okrągły i ruchy huśtawki, które charakteryzują się powtarzaniem.

Przykładami funkcji trygonometrycznych są:

• f (x) = sin x
• G (t) = 5⋅cos (ωt + π)
• H (x) = tg (x/2)

Zmienna X jest wyrażana w radiach.

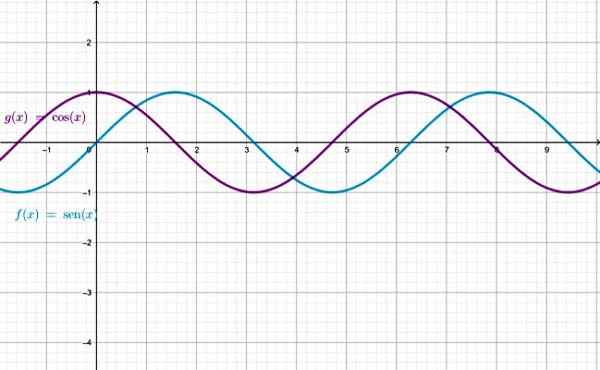Wykres funkcji Sen X i cos x, zauważ, że są one identyczne, z wyjątkiem tego, że jeden jest przesunięty w odniesieniu do drugiego. Źródło: f. Zapata przez Geogebra.

Mistrzostwo funkcji Sen X i Cos X jest zbiorem liczb rzeczywistych. Dla pozostałych funkcji istnieją x wartości, dla których funkcja nie jest zdefiniowana:

-Funkcja Tg X nie istnieje, gdy x = ± π /2, ± 5π /2 ... to jest wszystkie nieparzyste wielokrotności π /2.

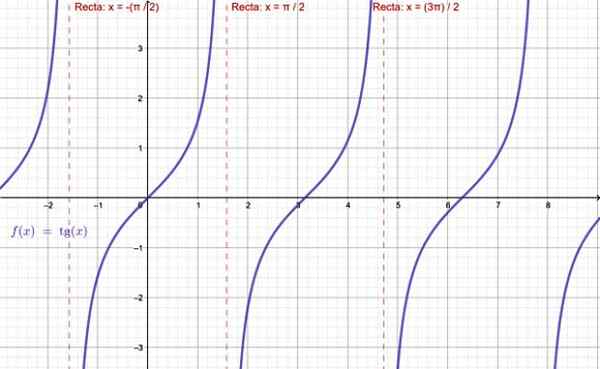Wykres funkcji stycznej. Źródło: f. Zapata przez Geogebra.

-Jeśli chodzi o f (x) = cotg x, ta funkcja nie jest zdefiniowana dla całych wielokrotności π: ± π, ± 2π, ± 3π ..

Może ci służyć: prawo znaków

-Funkcja y = sec x jest nieprawidłowa, gdy cos x = 0, co wyklucza x = ± π /2, ± 5π /2….

-Wreszcie dla f (x) = szkoda x, całe wielokrotności π nie należą do ich domeny.

Siema.2.D) Funkcje hiperboliczne

Funkcje hiperboliczne to specjalne kombinacje wykładniczych i^X i e^-X I są nazywani Bosom, Coseno .. .hiperboliczny. Podobnie jak w przypadku funkcji trygonometrycznych, zwanych również „okrągłym”, istnieje 6 funkcji hiperbolicznych:

-Zatok hiperboliczny Senh X:

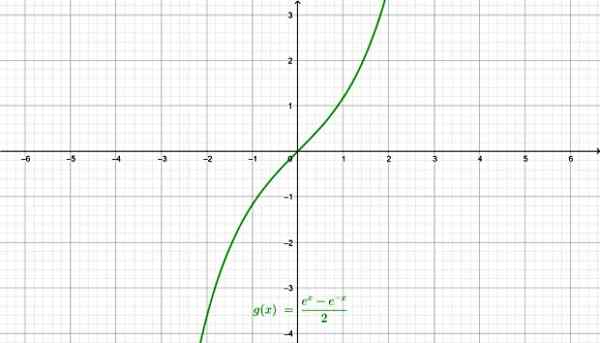Funkcja zatoki hiperbolicznej. Źródło: f. Zapata przez Geogebra.

-Hiperboliczny cosinus COSH X:

 -Styczna hiperboliczna Tanh X:

 -Hiperboliczne kombajn CSCH X:

 -Sevant hiperboliczny Sech x:

-Hiperboliczny Cotangent Coth X:

Elastyczny kabel, wykonany z munduru i wiszącego materiału między dwoma punktami, ma kształt krzywej nazywanej łańcuchowy, który jest wyrażany jako hiperboliczny cosinus:

Siema.2.e) Odwrotne funkcje trygonometryczne

Odpowiadają odwrotnie funkcji trygonometrycznych. Na przykład, jaki byłby kąt (ARC), którego bosom jest wart 0.5?

Odpowiedź to Arc Sen 0.5, który brzmi „Sinus łukowy 0.5 ”, a kąt ten wynosi 30º, choć zasadniczo nie byłby to jedyny kąt, którego bosom jest wart 0.5, ponieważ funkcja Sen X jest okresowa. To, co się stanie, to, że jeśli funkcja SEN X zostanie podjęta w całej jej domenie, nie miałaby odwrotnej, więc nie można było zdefiniować funkcji Arcoseno. Problem jest rozstrzygany przez ograniczenie wszystkiego do kątów między -π/2 i +π/2.

Można to wyrazić w następujący sposób:

Jeśli Arc Sen x = θ, oznacza to, że sin θ = x

Z -π/2 ≤ θ ≤ π/2.

Innym notacją stosowaną dla arc sen x jest f (x) = sin^-1 X. Wykres pokazano poniżej:

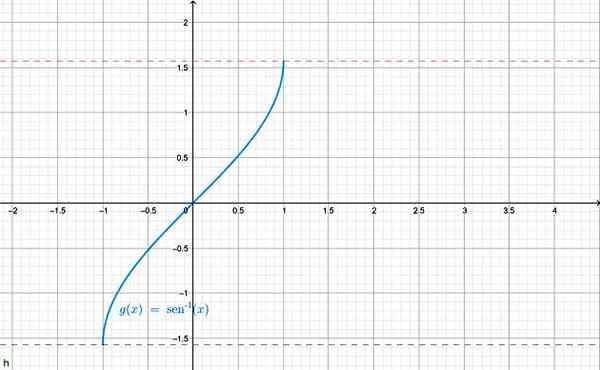Arcsen x Funkcja Graphics. Źródło: f. Zapata przez Geogebra.

Możliwe jest również zdefiniowanie odwrotności dla innych funkcji trygonometrycznych, na przykład: Arc cos x = θ. Dla każdego ranga jest prawidłowo ograniczona, aby być odwrotnością odpowiedniej funkcji trygonometrycznej.

Ii) funkcje zgodnie z symetrią

Ii.1) par

Jeśli dla wszystkich X należących do domeny f (x) jest spełnione, że:

f (x) = f (-x)

Mówi się, że funkcja jest równa, tak jak te, które następują:

• f (x) = x² - 3
• g (x) = cos x
• 

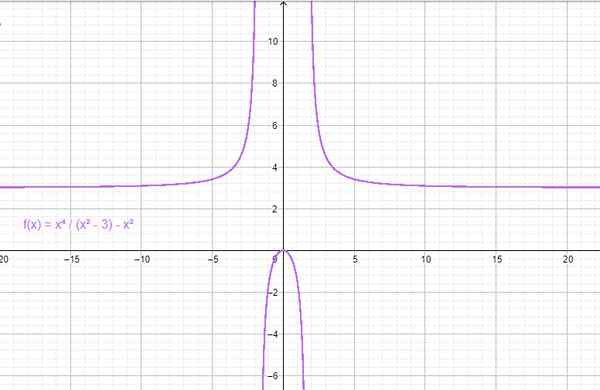  Przykład funkcji pary. Źródło: f. Zapata przez Geogebra.

Na przykład robienie x = 1 cala f (x) = x² - 3 otrzymuje:

f (1) = 1² - 3 = -2.

A jeśli x = -1, to:

f (-1) = (-1)² - 3 = -2.

Oba wyniki są identyczne.

Wyrównane funkcje mają symetrię wokół osi pionowej, jak widać na poprzedniej figurze.

Ii.2) Dziwna funkcja

Z drugiej strony tak:

f (-x) = -f (x)

Funkcja jest dziwna.

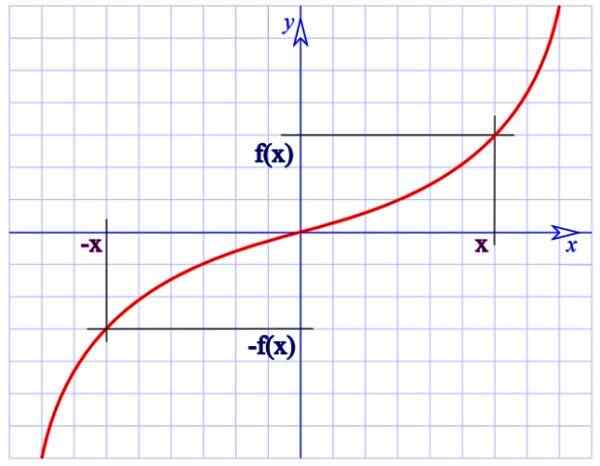Dziwna funkcja. Źródło: Wikimedia Commons.

Na przykład funkcja f (x) = 1/x górnej figury jest dziwna, ponieważ:

f (-x) = -1/x

I

-f (x) = -1/x

Inną ważną funkcją impar jest F (x) = sin x.

Należy zauważyć, że funkcje nieparzyste mają symetrię obrotu 180º wokół pochodzenia (wykres nie ulega zmianie, jeśli każdy jego punkt zostanie skręcony o 180º w odniesieniu do pochodzenia współrzędnych).

Iii) funkcja zgodnie z wyrażeniem zmiennej

Iii.1) Funkcje jawne

Są one wyrażane bezpośrednio w kategoriach zmiennej zależnej, takiej jak y = f (x). Na przykład:

• f (x) = x³

Iii.2) Niejawne funkcje

W funkcjach ukrytych żadna z zmiennych nie wydaje się jasne. Są one wyrażone jako f (x, y) = 0, takie jak:

• X² + I² -3xy = 0
• xy = - x²+ X-5

Funkcje opisane w tym artykule są funkcjami jawnymi.

Iv) funkcje zgodnie z grafiką

Zgodnie z ich wykresem funkcje mogą być ciągłe lub nieciągłe. Ciągłe funkcje można prześledzić bez przerywania udaru, z drugiej strony, nieciągłe funkcje obecne skoki. Na poniższym obrazie funkcja jest nieciągła przy x = a:

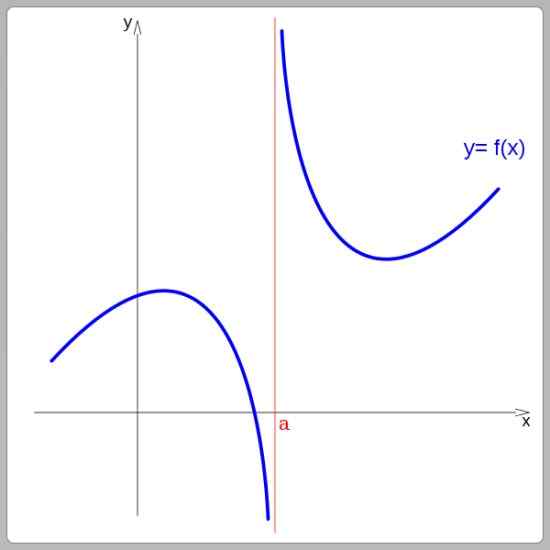Funkcja nieciągłości przy x = a. Źródło: Wikimedia Commons.

Przykładami funkcji ciągłych są funkcje liniowe, funkcje kwadratowe oraz funkcje sinusoidalne i cosinus. A wśród nieciągłych funkcji znajdują się rozłożona funkcja i funkcja styczna.

V) funkcje zgodnie z zależnością między elementami domeny a zakresem

V.1) Funkcja iniekcyjna

Funkcja jest Invicitive Gdy w zestawie domeny lub domeny nie ma dwóch różnych elementów, które mają ten sam obraz w zestawie przyjazdu.

Załóżmy, że rzeczywiste funkcje mają, o ile nie określono inaczej, na przykład:

f (x) = 5x -2

Cała wartość x należąca do domeny f (x), która jest zestawem ℛ liczb rzeczywistych, ma unikalny, również prawdziwy obraz. Z drugiej strony w tej drugiej funkcji:

g (x) = x²

Istnieją różne elementy w domenie, które mają ten sam obraz, na przykład x₁= 2 i x₂= -2:

G (2) = g (-2) = 4.

Sposobem identyfikacji funkcji incydentu z jej wykresu jest rysowanie linii poziomej, jeśli jest one odcięta na krzywą w więcej niż jednym punkcie, funkcja nie jest instrumentowa.

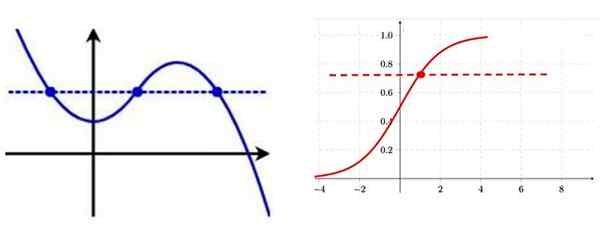Po lewej stronie nie incydentacji, zauważ, że istnieje kilka punktów wykresu z tą samą współrzędną pionową. Po prawej funkcji incydentu, w każdym z punktów krzywej ma określoną współrzędną „y”. Źródło: f. Zapata.

V.2) Funkcja zatrzymywania

w Funkcje onjective, Wszystkie elementy zestawu przybycia są obrazem jakiegoś elementu zestawu początkowego. Przykładem funkcji zatwierdzającej jest ten sam f (x) = 5x -2, ale g (x) = x² Tak nie.

Jednak domenę można było na nowo zdefiniować, aby G (x) była zatrzymująca, jeśli na przykład zmieni się na wszystkie pozytywne rzeczywiste plus 0. 

V.3) Funkcja biejcive

Wreszcie, nazywana jest funkcja, która jest zarówno iniekcyjna, jak i zatwierdzająca Bijecveive. Przykłady funkcji biejcive to: funkcja powiązana, funkcja wykładnicza i funkcja logarytmu.

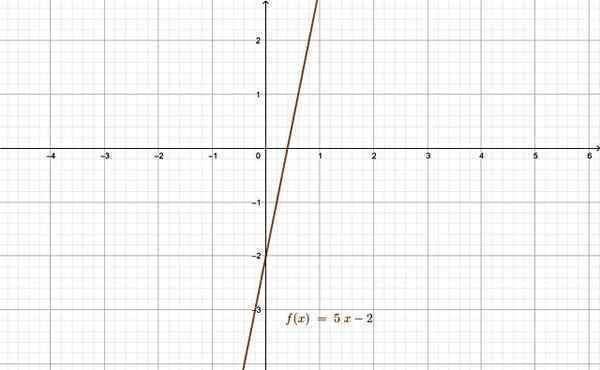Powiązana funkcja jest dobrym przykładem funkcji bijkłowców. Źródło: f. Zapata przez Geogebra.

Bibliografia

1. Strefa e-matem. Rodzaje funkcji. Odzyskany z: Emathzone.com.
2. Hoffman, J.G. Wybór problemów z matematyką. Wyd. SPPHINX.
3. Matematyka jest zabawna. Odniesienie funkcji Commons. Odzyskany z: Mathisfun.com.
4. Requena, ur. Formuły wszechświata. Rodzaje funkcji. Odzyskane z: Universoformulas.com.
5. Stewart, J. 2006. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.