Charakterystyka Teselados, typy (regularne, nieregularne), przykłady

 Tesselled Są to powierzchnie pokryte jedną lub więcej nazwami nazywanych Tessels. Są wszędzie: na ulicach i wszelkiego rodzaju budynkach. Tessels lub płytki są płaskimi kawałkami, zwykle wielokątami z przystającymi lub izometrycznymi kopiami, które są umieszczane zgodnie z regularnym wzorem. W ten sposób nie ma spacji bez objęcia, a płytki lub mozaiki nie nakładają się. 

W przypadku użycia pojedynczego typu mozaiki utworzonej przez zwykły wielokąt, wówczas istnieje Zwykły Tesseld, Ale jeśli używane są dwa lub więcej rodzajów zwykłych wielokątów, to jest to Pół -regularny tesselled.

Rysunek 1. Nieregularna podłoga podłogowa, ponieważ prostokąty są wielokątami nieregularnymi, nawet gdy są kwadraty. Źródło: Pixabay.

Wreszcie, gdy wielokąty, które tworzą Tesseldo, nie są regularne, więc jest to Nieregularny Tesselled.

Najczęstszym rodzajem teseldo jest ten utworzony przez prostokątne i szczególnie kwadratowe mozaiki. Na rycinie 1 mamy dobry przykład.

[TOC]

Historia Teselados

Tessellacja jest używana od tysięcy lat do pokrycia podłóg i ścian pałaców i świątyń różnych kultur i religii.

Na przykład cywilizacja sumeryjska, która rozkwitała około 3500 do.C. Na południe od Mezopotamii, między eufratami i rzekami Tigris, używali TESELE w swojej architekturze.

Rysunek 2. Teselados Sumerios przy drzwiach Istar. Źródło: Wikimedia Commons.

Tesels również wzbudziły zainteresowanie matematyków wszystkich czasów: zaczynając od Archimedesa w trzecim wieku pne, a następnie Johannes Kepler w 1619 r., Camille Jordan w 1880 roku, aż do współczesnych czasów z Rogerem Penrose.

Może ci służyć: ułamek równoważny 3/5 (rozwiązanie i wyjaśnienie)

Penrose stworzył nieobseriową tessellację znaną jako Penrose Tessellation. Ite To tylko niektóre nazwy naukowców, którzy dużo wnieśli wkład w tessellację.

Zwykłe Tesels

Zwykłe teslate są wykonane z jednego typu zwykłego wielokąta. Z drugiej strony, aby Tesseldo można uznać za zwykły cały punkt samolotu:

-Należy do wnętrza wielokąta

-Lub do krawędzi dwóch sąsiednich wielokątów 

-Wreszcie może należeć do wspólnego wierzchołka co najmniej trzech wielokątów.

Z powyższymi ograniczeniami można wykazać, że tylko trójkąty równoboczne, kwadraty i heksagony mogą tworzyć zwykły tessel.

Nomenklatura

Istnieje nomenklatura oznaczająca tesele, które składają się z listy w kierunku igieł zegara i oddzielona przez punkt, liczba boków wielokątów otaczających każdy węzeł (lub wierzchołek) tesselled, zawsze zaczynając od najmniejszej liczby boków.

Ta nomenklatura dotyczy regularnych i pół -regularnych tesselvów. 

Przykład 1: Trójkątny Teselado

Rycina 3 pokazuje trójkątną regularną płytkę. Należy zauważyć, że każdy trójkątny węzeł płytek jest wspólnym wierzchołkiem sześciu trójkątów równobocznych. 

Sposób oznaczania tego typu Tesseldo wynosi 3.3.3.3.3.3, co jest również oznaczone przez 3⁶.

Rysunek 3. Trójkątny regularny Teselado 3.3.3.3.3.3. Źródło: Wikimedia Commons

Przykład 2: Square Tessel

Rycina 4 pokazuje zwykłą płytkę złożoną tylko z kwadratów. Należy zauważyć, że każdy węzeł płytek jest otoczony czterema przystającymi kwadrami. Notacja, która dotyczy tego rodzaju kwadratowych tesselvów, to: 4.4.4.4 O naprzemiennie 4⁴

Rysunek 4. Square Tesseld 4.4.4.4. Źródło: Wikimedia Commons.

Przykład 3: Sześciokątny Tesseld

W sześciokątnej Tesselle. Nomenklatura regularnego sześciokątnego Tesselled to 6.6.6 O naprzemiennie 6³.

Może ci służyć: sekcje stożkowe: typy, aplikacje, przykłady Rysunek 5. Sześciokątny Tesseld 6.6.6. Źródło: Wikimedia Commons.

Pół -regularny tesselled

TESELE SEMI -regularne lub tesselled archimedes składa się z dwóch lub więcej rodzajów zwykłych wielokątów. Każdy węzeł jest otoczony rodzajami wielokątów, które składają się na tesselled w tej samej kolejności, a stan krawędzi całkowicie udostępniony są sąsiadowi.

Istnieje osiem pół -regularnych teselów:

1. 3.6.3.6 (Tri-hexagonal Tesselled)
2. 3.3.3.3.6 (sześciokątny Teslate Romo)
3. 3.3.3.4.4 (Elongado Triangular Teselado)
4. 3.3.4.3.4 (Romo Square Tesselled)
5. 3.4.6.4 (Rombi-tri-heksagonalny Tesseld)
6. 4.8.8 (skrócony kwadratowy tesselled)
7. 3.12.12 (ścięty sześciokątny Tesseld)
8. 4.6.12 (skrócony trójkagonalny Tesseld)

Niektóre przykłady pół -regularnego teslanu pokazano poniżej.

Przykład 4: Tixagonal Teselado

Jest to ten, który składa się z regularnych trójkątów równobocznych w strukturze 3.6.3.6, co oznacza, że ​​węzeł kafelkowy jest otoczony (dopóki nie zakończy powrotu) trójkątem, sześciokątem, trójkątem i sześciokątem. Rysunek 6 pokazuje taki tessel.

Rysunek 6. TRI-HEXGONAL TESSELD (3.6.3.6) Jest to przykład pół -regularnego tesselled. Źródło: Wikimedia Commons.

Przykład 5: Sześciokątny Tesseldo Romo

Podobnie jak płytki poprzedniego przykładu, składa się również z trójkątów i heksagonów, ale jego dystrybucja wokół węzła wynosi 3.3.3.3.6. Rycina 7 wyraźnie ilustruje ten rodzaj tesselled.

Rysunek 7. Sześciokątny Tesseldo Romo składa się z sześciokąta otoczonego 16 trójkątami w konfiguracji 3.3.3.3.6. Źródło: Wikimedia Commons.

Przykład 6: Rombi-tri-heksagonalny tessel

Jest to płytka, która składa się z trójkątów, kwadratów i sześciokątów, w konfiguracji 3.4.6.4, co pokazano na rycinie 8.

Cyfra 8. Pół -regularny tesselled złożony z trójkąta, kwadratu i sześciokątu w konfiguracji 3.4.6.4. Źródło: Wikimedia Commons.

Nieregularne Tesels

Są one nazywane nieregularnymi teselami do tych, które są tworzone przez nieregularne wielokąty lub przez zwykłe wielokąty, ale nie spełniają kryterium, że węzeł jest wierzchołkiem co najmniej trzech wielokątów.

Może ci służyć: antykiwatywne: formuły i równania, przykłady, ćwiczenia

Przykład 7

Rycina 9 pokazuje przykład nieregularnej płytki, w której wszystkie wielokąty są regularne i przystające. Jest to nieregularne, ponieważ węzeł nie jest wspólnym wierzchołkiem co najmniej trzech kwadratów, a także są sąsiednie kwadraty, które nie mają całkowicie przewagi.

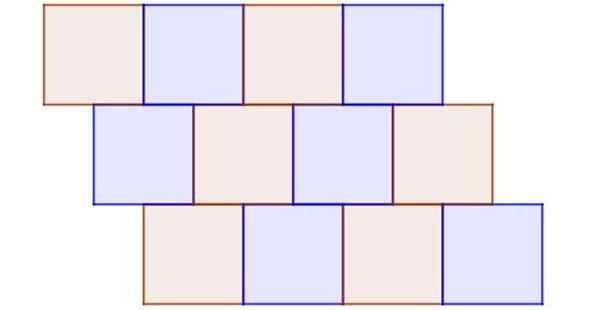Rysunek 9. Nawet gdy wszystkie płytki są przystającymi kwadrami, jest to wyraźny przykład nieregularnego tesselled. Źródło: f. Zapata.

Przykład 8

Równoległobok tee płaską powierzchnię, ale chyba, że ​​jest to kwadrat nie może utworzyć zwykłego tessela.

Rysunek 10. Tesseldo utworzone przez równoległoboki jest nieregularne, ponieważ jego mozaiki są wielokątami nieregularnymi. Źródło: f. Zapata.

Przykład 9

Nieregularne heksagony z centralną symetrią ustawiają płaską powierzchnię, jak pokazano na poniższym rysunku:

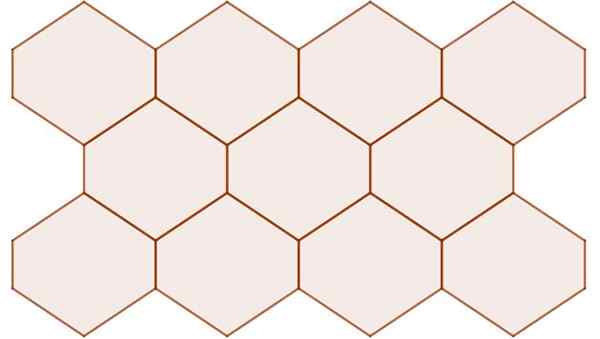Rysunek 11. Sześciokąt z centralną symetrią, nawet jeśli nie są regularne, ustawiają samolot. Źródło: f. Zapata.

Przykład 10: El Cairo Teselado

Jest to bardzo interesująca tessellacja, złożona z pięciokrotnych boków równej długości, ale z nierównymi kątami, z których dwa są proste, a pozostałe trzy mają 120º każdy każdy.

Powiada się, że ten Tesseld jest w chodniku niektórych ulic Kairu w Egipcie. Rycina 12 pokazuje Tesseldo z Kairu.

Rysunek 12. Cairo Tesseldo. Źródło: Wikimedia Commons.

Przykład 11: Teselado al-Andalus

Tesseldo podczas niektórych części Andaluzji i Afryki Północnej charakteryzują się geometrią i epigrafią, oprócz elementów ozdobnych, takich jak roślinność. 

Tesselled Palacios, takie jak Alhambra złożona z płytek utworzonych przez ceramiczne kawałki wielu kolorów, z wieloma (nie mówiąc o nieskończoności) form, które wywołały wykresy geometryczne.

Rysunek 13. Teselado Palacio de la alhambra. Tartaglia / domena publiczna

Przykład 12: Teselado w wideo

Znany również jako Tesellation, jest to jeden z najbardziej boomów w grach wideo. Jest to tworzenie tekstur do symulacji teselda różnych scenariuszy, które pojawiają się w symulatorze.

Jest to wyraźna refleksja, że ​​okładki te nadal ewoluują, przenosząc granice rzeczywistości.

Bibliografia

1. Ciesz się matematyką. Tesels. Odzyskane z: FaveMatimaticas.com
2. Rubiños. TESELE rozwiązały przykłady. Odzyskane z: matematyki.Blogspot.com
3. Weisstein, Eric W. „Deiregula tessellation”. Weisstein, Eric W, Ed. Mathworld. Wolfram Research.
4. Wikipedia. Tesselled. Odzyskane z: jest.Wikipedia.com
5. Wikipedia. Zwykły Tesseld. Odzyskane z: jest.Wikipedia.com