Zielone twierdzenie, demonstracja, zastosowania i ćwiczenia

On Zielone twierdzenie Jest to metoda obliczeniowa stosowana do powiązania całek linii z podwójnym obszarem lub całkami powierzchniowymi. Zaangażowane funkcje muszą być oznaczone jako wektor i zdefiniowane pola w trajektorii C.

Na przykład wyrażenie linii integralnej może być bardzo skomplikowane w rozwiązaniu; Jednak podczas wdrażania twierdzenia Greena podwójne całki stają się dość podstawowe. Zawsze ważne jest, aby szanować pozytywne poczucie trajektorii, odnosi się to do kierunku igieł zegarowych.

Twierdzenie Greena jest szczególnym przypadkiem twierdzenia Stokesa, w którym projekcja funkcji wektorowej jest przeprowadzana w płaszczyźnie XY.

[TOC]

Definicja

Wyrażenie Twierdzenia Greena jest następujące:

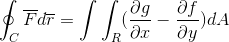
W pierwszym okresie obserwuje się całkowanie linii zdefiniowane przez trajektorię „C”, skalarnego produktu między funkcją wektora „F” a funkcją wektora „R”.

C: Jest to zdefiniowana trajektoria, na której funkcja wektora będzie rzutowana, o ile zostanie zdefiniowana dla tej płaszczyzny.

F: Funkcja wektora, w której każdy z jego składników jest zdefiniowany przez funkcję jako taką (F, G).

Odp. W takim przypadku działa z różnicą tego wektora.

W drugim terminie obserwuje się zielone twierdzenie, w którym obserwuje się podwójna całka zdefiniowana w regionie R różnicy częściowych pochodnych G i F, w odniesieniu do x i i odpowiednio. Dla różnicy obszaru, który jest niczym więcej niż produktem obu różnicowych różnic (DX.dy).

To twierdzenie ma idealnie zastosowanie do całek przestrzeni i powierzchni.

Demonstracja

Aby zademonstrować twierdzenie Greena w prosty sposób, zadanie to zostanie podzielone na 2 części. Najpierw założymy, że funkcja wektora F ma tylko definicję w wersji Siema. Podczas gdy funkcja „g” odpowiadająca versorowi J będzie równe zero.

Może ci służyć: ile setnych pasuje w ciągu jednej dziesiątej? (Przykłady)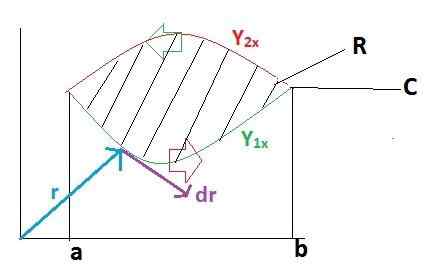Autor

F = f (x, y)Siema + G (x, y)J = f (x, y)Siema + 0

R = xSiema + IJ

DR = DXSiema + DyJ

Najpierw opracowujemy całkę linii w stosunku do trajektorii C, dla której trajektoria została rozegrana w 2 sekcjach, które przechodzą pierwsze z A do B i po B do A.

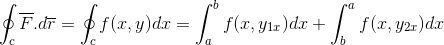
Zastosowana jest definicja podstawowego twierdzenia o obliczeniach dla zdefiniowanej całki.

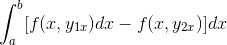
Wyrażenie jest przełożone w pojedynczej całce, jest wspólne dla negatywnych, a kolejność czynników jest odwrócona.

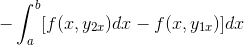
Przez szczegółowe obserwowanie tego wyrażenia staje się oczywiste, że przy stosowaniu kryteriów funkcji prymitywnej jest ono w obecności całki wyrażenia pochodzącego z F w odniesieniu do i. Oceniane w parametrach

[I_1x , I_2x]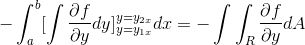

Teraz wystarczy założyć, że funkcja wektorowa jest zdefiniowana tylko dla G (x, y)J. Gdzie działając w sposób homologowany do poprzedniej sprawy, jest to uzyskiwane:

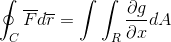
Wreszcie, 2 demonstracje są pobierane i dołączają w przypadku, gdy funkcja wektora przyjmuje wartości dla obu wersji. W ten sposób jest to pokazane jako całka linii po zdefiniowaniu i uznaniu jako jednowymiarowa trajektoria, może być w pełni rozwinięta dla płaszczyzny i przestrzeni.

F = f (x, y)Siema + G (x, y)J

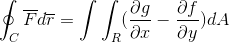
W ten sposób wykazano twierdzenie Greena.

Aplikacje

Zastosowania zielonego twierdzenia są szerokie w gałęziach fizyki i matematyki. Rozciągają się one na dowolną aplikację lub zastosowanie, które można podać do integracji linii.

Prace mechaniczne wykonywane siłą F poprzez trajektorię C można opracować za pomocą całki linii, która jest wyrażona jako podwójna całka obszaru przez twierdzenie Greena.

Może ci służyć: Pentagonowy pryzmat: Charakterystyka, części, wierzchołki, krawędzie, objętość

Momenty bezwładności wielu ciał poddanych siłom zewnętrznym w różnych punktach zastosowania, również reagują na opracowalne całki z twierdzeniem Greena.

Ma to wiele funkcji w badaniach oporowych używanych materiałów. Gdzie wartości zewnętrzne można określić ilościowo i wziąć pod uwagę przed opracowaniem różnych elementów.

Ogólnie rzecz biorąc, twierdzenie Greena ułatwia zrozumienie i definicję obszarów, w których funkcje wektorowe są określone w odniesieniu do regionu zgodnie z trajektorią.

Historia

Został opublikowany w 1828 roku w pracy Analiza matematyczna dla teorii energii elektrycznej i magnetyzmu, Napisane przez brytyjskiego matematyka George'a Greena. Bada dość decydujące sekcje zastosowania obliczeń w fizyce, takie jak koncepcja potencjału, funkcje zielonego i zastosowania jego twierdzenia auto zatytułowanego.

George Green sformalizował swoją karierę studencką w wieku 40 lat, jak dotąd całkowicie samozadowolenia matematyka. Po studiach na University of Cambridge jego badania trwają, wkład w dziedzinę akustyki, optyki i hydrodynamiki, które są nadal obowiązujące.

Związek z innymi twierdzeniami

Twierdzenie Greena jest szczególnym przypadkiem i wynika z 2 innych bardzo ważnych twierdzeń w oddziale obliczeniowym. To są twierdzenie Kelvina-Stokesa i rozbieżność lub twierdzenie Gausskiego.

Począwszy od dowolnego z obu twierdzeń, że możesz dotrzeć do twierdzenia Greena. Pewne definicje i propozycje są konieczne do opracowania tych demonstracji.

Ćwiczenia

- Poniższe ćwiczenie pokazuje, jak przekształcić całkę linii w podwójną całkę w odniesieniu do regionu R.

Oryginalne wyrażenie jest następujące:

Może ci służyć: ile warto x?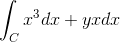

I należy być oceniany w regionie trójkątnym, który łączy punkty (0, 0), (1, 0), (0, 1) oznaczone przez c. W tym przypadku zostanie rozważone pozytywne poczucie zakrętu.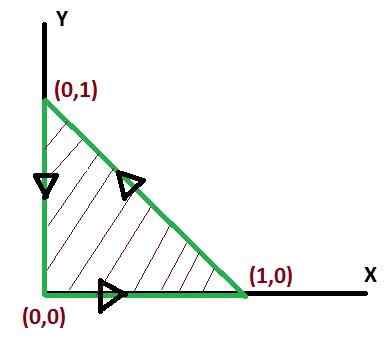

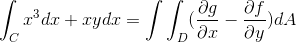
Skąd są pobierane funkcje odpowiadające F i G

f (x, y) = x³                      g (x, y) = yx

df/dy = 0 dg/dx = y

Ważne jest, aby zdefiniować funkcje, które składają się na granice regionu C, aby móc złożyć różnicowy produkt, który całkowicie pokryje region.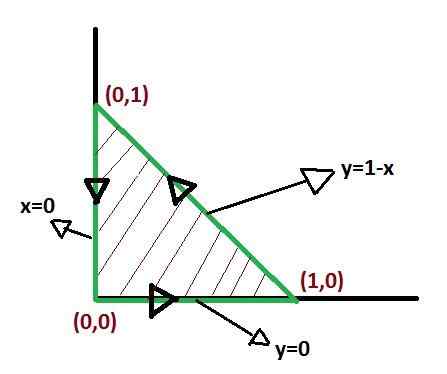

Nie ma unikalnego sposobu zdefiniowania limitów integracji przy stosowaniu twierdzenia Greena. Ale istnieją formy, w których całki po zdefiniowaniu mogą być prostsze. W taki sposób, że optymalizacja limitów integracji zasługuje na uwagę.

W tym przypadku to wyrażenie jest rozważane: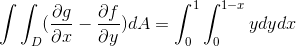

Gdzie w rozwiązywaniu całek, które otrzymujemy:

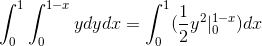
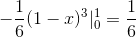
Wartość ta odpowiada jednostkom sześciennym w regionie poniżej funkcji wektora i na regionie trójkątnym zdefiniowanym przez C.

W przypadku całki linii bez wykonywania zielonej metody konieczne byłoby parametryzację funkcji w każdej sekcji regionu. To znaczy, że 3 sparametryzowane całki do rozdzielczości. Jest to wystarczający dowód skuteczności, który Robert Green przyczynił się do swojego twierdzenia do obliczeń.

Bibliografia

1. Wprowadzenie do mechaniki ciągłej. W Michael Lai, David H. Rubin, Erhard Krempl, David Rubin Butterworth-Heinemann, 23 lipca. 2009
2. Rachunek wielowymiarowy. James Stewart. Cengage Learning, 22 marca. 2011
3. Nieformalna historia twierdzenia Greena i powiązanych pomysłów. James Joseph Cross. Department of Mathematics, University of Melbourne, 1975
4. Zachowanie cieplne za pomocą funkcji zieleni. Kevin d. Cole, James V. Beck, a. Haji-Sheikh, Bahman Luckouhi. Taylor i Francis, 16 lipca. 2010
5. Zastosowanie twierdzenia Greena do ekstremalizacji integral liniowych. Centrum Informacji Technicznej obrony, 1961