Teoria zbiorów charakterystyk, elementy, przykłady, ćwiczenia

Ustaw teorię Jest to gałąź logicznej matematyki, która jest odpowiedzialna za badanie relacji między podmiotami zwanymi zestawami. Zestawy charakteryzują się byciem kolekcjami obiektów tego samego rodzaju. Te obiekty są elementami zestawu i mogą być: liczby, litery, liczby geometryczne, słowa reprezentujące obiekty, obiekty i inne.

To był Georg Cantor pod koniec XIX wieku, zaproponował zestaw zestawów. Podczas gdy inni godne uwagi matematycy w XX wieku dokonali sformalizowania: Gottlob Frege, Ernst Zermelo, Bertrand Russell, Adolf Fraenkel.

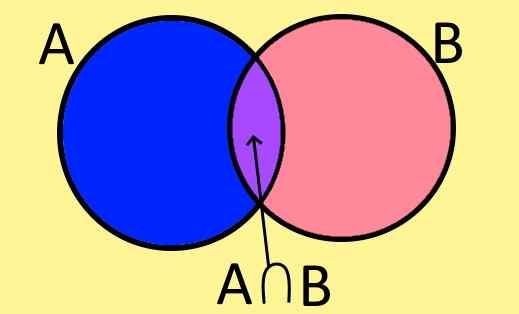
Rysunek 1. Schemat Venna zestawów A, B i ich skrzyżowanie A⋂ B. (Własne opracowanie).

Schematy Venna są graficznym sposobem reprezentowania zestawu i składa się z zamkniętej płaskiej postaci, w której znajdują się elementy zestawu.

Na przykład ryc. 1 pokazuje dwa zestawy A i B, które mają wspólne elementy, elementy wspólne dla A i B. Tworzą one nowy zestaw zwany zestawem przecięcia A i B, który jest napisany symbolicznie w następujący sposób:

A ∩ B

[TOC]

Charakterystyka

Zestaw jest prymitywną koncepcją, ponieważ w geometrii koncepcja punktu, prosta lub płaska. Nie ma lepszego sposobu na wyrażenie koncepcji niż wskazanie przykładów: 

Zestaw i utworzony przez kolory flagi Hiszpanii. Ten sposób wyrażania zestawu jest nazywany zrozumieniem. Ten sam zestaw i napisane przez rozszerzenie to:

E = czerwony, żółty

W takim przypadku czerwone i żółte są elementami zestawu i. Należy zauważyć, że elementy są wymienione między klawiszami i nie są powtarzane. W przypadku hiszpańskiej flagi znajdują się trzy paski kolorów (czerwony, żółty, czerwony) z których dwa są powtarzane, ale elementy nie są powtarzane po wyrażaniu zestawu.

Załóżmy zestaw V utworzony przez pierwsze trzy litery wokalne:

V = a, e, i

Moc V, która jest oznaczona przez p (v), jest zestawem wszystkich zestawów, które można uformować za pomocą elementów V:

P (v) = a, e, i, a, e, a, i, e, i, a, e, i

Rodzaje zestawów

Zestaw skończony

Jest to zestaw, w którym jego elementy są liczne. Przykładami skończonych zestawów są litery hiszpańskiego alfabetu, samogłoski hiszpańskie, planety Układu Słonecznego. Liczba elementów skończonego zestawu nazywa się jego kardynalnością.

Nieskończony zestaw

Nieskończony zespół, każdy, kto liczba jego elementów jest bezczelna, ponieważ niezależnie od tego, jak duża liczba jego elementów jest zawsze możliwa do znalezienia większej liczby elementów.

Nieskończonym przykładem zestawu jest zbiór liczb naturalnych N, który jest szeroko wyrażany w następujący sposób:

Może ci służyć: Koplanares Punkty: Równanie, przykład i rozwiązane ćwiczenia

N = 1, 2, 3, 4, 5, .. . jest wyraźnie nieskończony zestaw, ponieważ nie ma znaczenia, jak duża może być liczba naturalna, następujący kierunek zawsze może znaleźć w niekończącym się procesie. Oczywiście kardynał nieskończonego zestawu wynosi ∞.

Pusty zestaw

Jest to zestaw, który nie zawiera żadnego elementu. Pusty zestaw V jest oznaczony przez Ø lub za pomocą pary klawiszy bez elementów w środku:

V = = Ø.

Pusty zestaw jest unikalny, dlatego musi być nieprawidłowe powiedzenie „pustego zestawu”, właściwym formularzem jest powiedzenie „pustego zestawu”.

Wśród właściwości pustego zestawu jest to, że jest to podzbiór każdego zestawu:

Ø ⊂ a

Ponadto, jeśli zestaw jest podzbiorem pustego zestawu, ten zestaw koniecznie będzie pustką:

A ⊂ Ø ⇔ a = Ø

Zestaw jednolity

Nazywa się to zestawem jednolitowym dowolnym zestawem zawierającym pojedynczy element. Na przykład zestaw naturalnych satelitów Ziemi jest zestawem jednostkowym, którego jedynym elementem jest księżyc. Zestaw B liczb całkowitych mniejszych niż 2 i większy niż zero ma tylko element 1, dlatego jest to zestaw jednostkowy.

Zestaw binarny

Zestaw jest binarny, jeśli ma tylko dwa elementy. Na przykład ustaw x, tak że x jest rzeczywistą liczbą x^2 = 2 = 2. Ten zestaw według rozszerzenia jest napisany w ten sposób:

X = -√2, +√2

Uniwersalny zestaw

Zestaw uniwersalny to zestaw, który zawiera inne zestawy tego samego rodzaju lub natury. Na przykład uniwersalny zestaw liczb naturalnych jest zestawem liczb rzeczywistych. Ale liczby rzeczywiste są również uniwersalne liczb całościowych i racjonalnych.

Główne elementy

- Relacje między zestawami

W zestawach możesz ustalić kilka rodzajów relacji między nimi a ich elementami. Jeśli dwa zestawy a i b mają dokładnie te same elementy, wśród nich równa relacja jest oznaczona w następujący sposób:

DO = B

Jeśli wszystkie elementy zestawu do należącego do zestawu B, ale nie wszystkie elementy B należą do A, wówczas spośród tych zestawów istnieje związek włączenia, który jest oznaczony w następujący sposób:

A ⊂ b, ale b ⊄ a

Poprzednie wyrażenie brzmi: A jest podzbiorem B, ale B nie jest podzbiorem A.

Aby wskazać, że niektóre lub niektóre elementy należą do zestawu, są używane symbol przynależności ∈, na przykład stwierdzenie, że element lub elementy należą do zestawu A jest napisane symbolicznie w następujący sposób:

x ∈ A

Tak, element i nie należy do zestawu do tego związku, jest napisane w ten sposób:

i ∉ a

Relacja przynależna jest podana między elementami zestawu a zestawem, z wyłącznym wyjątkiem zestawu mocy, zbiorem jest kolekcja lub zestaw wszystkich możliwych zestawów, które można uformować za pomocą elementów wspomnianego zestawu.

Może ci służyć: czynnikowanie

Załóż, że v = a, e, i, twoja moc to p (v) = a, e, i, a, e, a, i, e, i, a, e, i, w takim przypadku zestaw v staje się elementem zestawu p (v) i można go zapisać:

V ∈ P (v)

- Właściwości włączenia

Pierwsza właściwość włączenia stwierdza, że ​​każdy zestaw jest zawarty sam w sobie, lub innymi słowy, co jest podzbiorem samego:

A ⊂ a

Inną właściwością włączenia jest przechodność: jeśli A jest z kolei podzbiór B i B, jest to podzbiór C, to A jest podzbiorem C. Smakowe relacja z przechodnością jest napisana w ten sposób:

(A ⊂ b) ^ (b ⊂ c) => a ⊂ c

Poniżej znajduje się schemat Venna odpowiadający przechodniejszności:

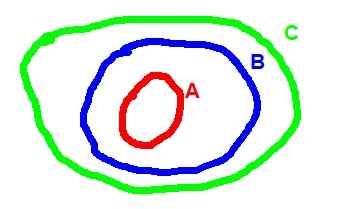Rysunek 2. (A ⊂ b) ^ (b ⊂ c) => a ⊂ c

- Operacje między zestawami

Skrzyżowanie

Przecięcie to operacja między dwoma zestawami, która powoduje nowy zestaw należący do tego samego uniwersalnego zestawu dwóch pierwszych. W tym sensie jest to operacja zamknięta.

Symbolicznie operacja przecięcia jest sformułowana w następujący sposób:

A⋂b = x / x∈A ^ x∈B

Przykład jest następujący: Ustaw A liter w słowie „elementy” i ustawiaj B liter słowa „powtarzane”, przecięcie między A i B jest napisane w ten sposób:

A⋂b = e, l, m, n, t, s ⋂ r, e, p, t, i, d, o, s = e, t, s . Uniwersalny zestaw A, z B, a także A⋂B jest zestawem liter hiszpańskiego alfabetu.

Unia

Związek dwóch zestawów to zestaw utworzony przez elementy wspólne dla dwóch zestawów i niekommonowych elementów dwóch zestawów. Operacja Unii między zestawami jest wyrażona symbolicznie w następujący sposób:

A∪b = x/x∈A v x∈B

Różnica

Działanie zestawu przynajmniej zestaw jest oznaczone przez A-B. A-B to nowy zestaw utworzony przez wszystkie elementy, które są w A i które nie należą do B. Symbol jest napisany w ten sposób:

A - b = x/ x ∈ A ^ x ∉ B

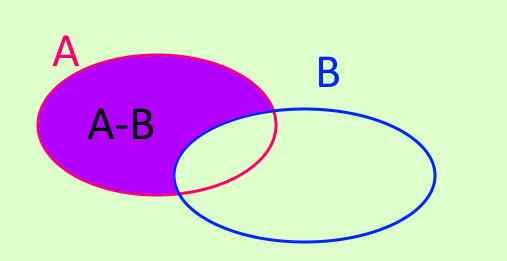Rysunek 3. A - b = x/ x ∈ A ^ x ∉ B

Różnica symetryczna

Różnica symetryczna to operacja między dwoma zestawami, w których wynikowy zestaw składa się z elementów, które nie są wspólne dla dwóch zestawów. Symetryczna różnica symbolicznie jest reprezentowana w następujący sposób:

A⊕b = x/ x∈ (a-b) ^ x∈ (B-a)

Przykłady

Przykład 1

Schemat Venna to graficzny sposób reprezentowania zestawów. Na przykład zestaw C liter zestawu słów jest reprezentowany w następujący sposób:

Przykład 2

Poniżej pokazano za pomocą diagramów Venna, że ​​zestaw samogłosek w słowie „zestaw” jest podzbiorem zestawu liter słowa „Ustaw”.

Może ci służyć: pobieranie próbek kwot: metoda, zalety, wady, przykłady

Przykład 3

Ustawić N Z liter hiszpańskiego alfabetu jest to zestaw skończony, ten zestaw jest napisany w ten sposób:

N = A, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, W, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, W, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, x, y, z i to Kardinalność wynosi 27.

Przykład 4

Ustawić V Z samogłosek w języku hiszpańskim jest to podzbiór zestawu:

V ⊂ N Dlatego jest to skończony zestaw.

Zestaw skończony V Rozszerzony sposób, w jaki jest napisane w ten sposób: V = a, e, i, o, u, a jej kardynał wynosi 5.

Przykład 5

Biorąc pod uwagę zestawy a = 2, 4, 6, 8 i b = 1, 2, 4, 7, 9 określić A-B i B-A. 

A - b są elementami, których nie są w B:

A - b = 6, 8

B - A są elementami B, które nie są w:

B - a = 1, 7, 9

Rozwiązane ćwiczenia

Ćwiczenie 1

Napisz symbolicznie, a także przedłużając płatek P liczby naturalnych nawet niższy niż 10.

Rozwiązanie: P = xof N / x < 10 ^ x mod 2 = 0

P = 2, 4, 6, 8

Ćwiczenie 2

Załóżmy, że całość utworzona przez liczby naturalne, które są czynnikami 210, a zestaw B, który powstał przez kuzyny liczb naturalnych niższy niż 9. Określ oba zestawy po rozszerzeniu i ustal, jakie są relacje między tymi dwoma zestawami.

Rozwiązanie: Aby określić elementy zestawu A, musisz zacząć od znalezienia czynników naturalnej liczby 210:

210 = 2 * 3 * 5 * 7

Następnie Set A jest napisane:

A = 2, 3, 5, 7

Rozważamy zestaw B, który jest kuzynami mniejszymi niż 9. 1 nie jest kuzynem, ponieważ nie spełnia definicji kuzyna: „Liczba jest kuzynem, jeśli i tylko wtedy, gdy ma dokładnie dwa dzielniki, 1 i sama liczba”. 2 jest parzyste, a jednocześnie kuzyna, ponieważ spełnia definicję kuzyna, pozostali kuzyni mniejsi niż 9 to 3, 5 i 7. Więc ten zestaw B jest:

B = 2, 3, 5, 7

Dlatego dwa zestawy są takie same: a = B.

Ćwiczenie 3

Określić zestaw, którego elementy x różnią się od x.

Rozwiązanie: C = x / x ≠ x

Jak każdy element, liczba lub obiekt jest równy sobie, zestaw C nie może być inny niż pusty zestaw:

C = Ø

Ćwiczenie 4

Być zestawem N liczb naturalnych i z zestawem liczb całkowitych. Określić n ⋂ z y n ∪ z.

Rozwiązanie: 

N ⋂ Z = x ∈ Z / x ≤ 0 = (-∞, 0]

N ∪ z = z ponieważ n ⊂ z.

Bibliografia

1. Garo, m. (2014). Matematyka: równania kwadratowe: jak rozwiązać równanie kwadratowe. Marilù Garo.
2. Haeussler, e. F., I Paul, r. S. (2003). Matematyka administracji i ekonomii. Edukacja Pearsona.
3. Jiménez, J., Rodríguez, m., Estrada, r. (2005). Matematyka 1 września. Próg.
4. Precious, c. T. (2005). Kurs matematyki 3o. Progreso redakcyjne.
5. Mathematics 10 (2018). „Przykłady skończonych zestawów”. Źródło: Mathematics10.internet
6. Wikipedia. Ustaw teorię. Odzyskane z: jest.Wikipedia.com