Suma wektorów metoda graficzna, przykłady, rozwiązane ćwiczenia

suma wektorów Jest to operacja dodawania między wektorami, która powoduje inny wektor. Wektory charakteryzują się wielkością, a także kierunkiem i znaczeniem. Dlatego ogólnie nie jest możliwe dodawanie ich tak, jak zrobiłoby to z wielkościami skalarnymi, to znaczy dodawaniem liczb.

Wektor uzyskany z sumy kilku wektorów jest nazywany wynikowy wektor. W mechanice rozmawiamy o wynikowa siła, która jest sumą wektorową wszystkich sił na ciele. Ten wynik jest równoważny z zestawem lub systemem sił.

Aby całkowicie określić wektor sumy, konieczne jest wskazanie wielkości i jedności, kierunku i znaczenia.

Ważne jest, aby podkreślić, że dodając wektory, muszą one reprezentować tę samą wielkość fizyczną, dlatego suma wektora jest jednorodną operacją. Oznacza to, że możemy dodać jedną siłę z drugą, ale nie siłą z przemieszczeniem, ponieważ wynik jest bez znaczenia.

Dostępnych jest kilka metod, aby znaleźć wynikowy wektor: grafika i analizy. Aby znaleźć sumy wektorowe za pomocą metod graficznych, opiera się on na prostej reprezentacji wektora, a mianowicie zorientowanej na segment lub strzałkę:

Graficzna reprezentacja wektora w płaszczyźnie. Źródło: f. Zapata.

Wektory są oznaczone czarnymi literami w drukowanym tekście lub strzałką nad literą, aby odróżnić je od odpowiednich wielkości lub wielkości skalarnych. Na przykład wielkość wektora v To jest po prostu v.

[TOC]

Metoda graficzna do dodawania wektorów

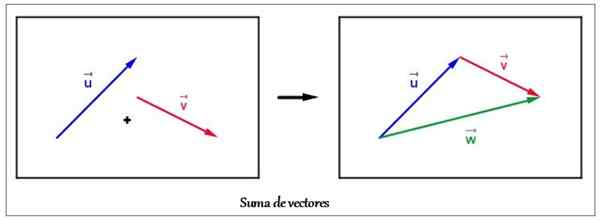
Aby dodać więcej niż dwa wektory kupletów, Metoda wielokąta albo wielokąt, który polega na przeniesieniu się do każdego z adresowanych wektorów. Cechą wektorów jest to, że są one niezmienne w odniesieniu do tłumaczenia, dlatego użyjemy tej właściwości do ustalenia sumy.

Może ci służyć: rozszerzenie termiczne

Zaczyna się od dowolnego z wektorów, ponieważ dodatek wektorowy jest komutowany, a kolejność dodatków nie zmienia sum. Drugi wektor porusza się poniżej, dopasowując swoje pochodzenie do końca pierwszego.

Następnie zostaje wprowadzony do następnego wektora, a następnie umieszcza tę samą procedurę, która ma dopasować pochodzenie do końca poprzedniego. W ten sposób przystąpimy do pozycjonowania ostatniego wektora.

Powstały wektor to ten, który łączy pochodzenie pierwszego z wolnym końcem ostatniego. Nazwa tej metody pochodzi od liczby, która wynika: wielokąt.

Przykład

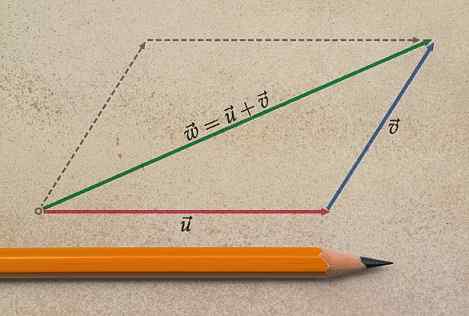
Sum przykład dwóch wektorów w płaszczyźnie metodą graficzną. Źródło: Wikimedia Commons

Weźmy jako przykład sumę dwóch wektorów Lub I v to pokazane na górnej figurze.

Zaczynając od wektora Lub, Przeniósł się do wektora v Aby dopasować jego pochodzenie do końca pierwszego. Powstały wektor W Jest wyciągany z pochodzenia Lub do końca v, tworząc trójkąt trzypasowy: trójkąt. Dlatego w tym szczególnym przypadku wywoływana jest procedura Metoda trójkąta.

Zwróć uwagę na ważny szczegół, wielkość lub moduł powstałego wektora nie jest sumą modułów dodatkowych wektorów. W rzeczywistości jest prawie zawsze mniej, chyba że wektory są równoległe.

Zobaczmy poniżej, co się stanie w tym przypadku.

Specjalny przypadek: suma wektorów równoległych

Opisaną metodę można również zastosować do specjalnego przypadku, w którym wektory są równoległe. Rozważ następujący przykład:

Może ci służyć: Boltzmann stała: historia, równania, obliczenia, ćwiczeniaSuma równoległych wektorów. Źródło: f. Zapata.

Wektor jest pozostawiony v W pierwotnej pozycji i przechodzi do wektora Lub w taki sposób, że jego pochodzenie zgadza się z końcem  v. Teraz wektor jest wyciągany z pochodzenia v I koniec Lub.

Jest to wynikowy wektor W a jego rozmiar jest sumą rozmiarów reklam. Kierunek i kierunek trzech wektorów jest taki sam.

Powstały wektor ma maksymalny moduł, jeśli dodatki tworzą kąt 0º, na przykład z przykładu. Jeśli wektory tworzą ze sobą kąt 180º, wynikowy wektor ma minimalny moduł.

Przykłady sumy wektorów

- Przemieszczenia

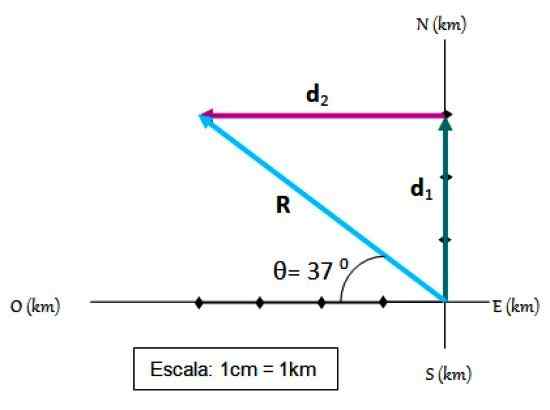
Rowerzysta podróżuje najpierw 3 km na północ, a następnie 4 km na zachód. Twoje przemieszczenie, które nazywamy R, Można go łatwo znaleźć za pomocą metody trójkąta plus system odniesienia, w którym oznaczone są punkty kardynalne:

Wynikające z dwóch przemieszczeń. Źródło: f. Zapata.

Kroki, aby dodać wektor

-Punkt początkowy zbiega się z pochodzeniem systemu odniesienia.

-Na osie współrzędnych wybiera się skala, która w tym przypadku wynosi 1 cm = 1 km

-Pierwsze przemieszczenie jest rysowane na skalę D_1.

-Następnie D₁ Drugie przemieszczenie jest narysowane D₂, Również na skalę.

-Powstałe przemieszczenie R Jest to wektor, który przechodzi od pochodzenia do końca D₂.

-Rozmiar R Jest mierzony za pomocą reguły stopniowej, łatwo jest sprawdzić, czy r = 5.

-Wreszcie kąt to R Forma z poziomym jest mierzona za pomocą transportera i okazuje się, że θ = 37 ⁰

- Wynikowa prędkość

Pływak chce przekroczyć rzekę i za to nic z prędkością 6 km/h, prostopadłe do brzegu, ale prąd, który niesie prędkość 4 km/h.

Może ci służyć: Ohm: Mierniki oporowe, przykłady i ćwiczenia rozwiązane

Aby poznać jego wynikową prędkość, dodawane są wektory prędkości pływaka, które zostały narysowane pionowo i prąd, który jest pozioma.

Zgodnie z metodą graficzną uzyskuje się wynikową prędkość v_R:

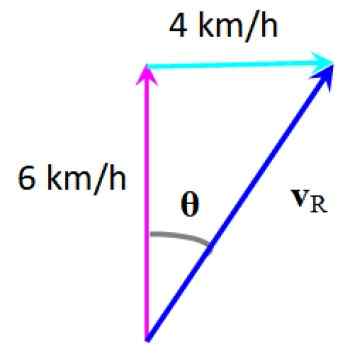Wynikowa prędkość. Źródło: f. Zapata.

Odchylenie doświadczane przez pływaka można obliczyć przez:

θ = ARCTG (4/6) = 33.7 po prawej stronie pierwszego adresu

Wielkość jego prędkości rośnie, ponieważ prędkość rzeki dodaje wektorowo. Możesz znaleźć ostrożnie skalę, jak w poprzednim przykładzie.

Lub za pomocą trygonometrycznych przyczyn 33.7:

Sen 33.7th = 4/v_R

v_R = 4/ sin 33.7. = 7.21 km/h

Ćwiczenie rozwiązane

Na cząsteczce następujące siły Ustawa, których wielkości wymieniono poniżej:

F₁= 2.5 N; F₂= 3 N; F₃= 4 N; F₄= 2.5 n

Znajdź wynikową siłę.

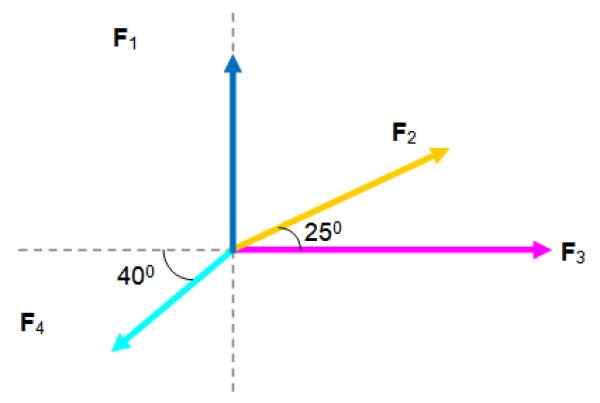System sił Coplanar. Źródło: f. Zapata.

Rozwiązanie

Możemy dodać graficznie zaczynając od dowolnego z wektorów, ponieważ suma wektora jest przemienna.

Na rysunku zaczęło się od F₁. Ustanowienie skali i przy pomocy reguły i oddziału pozostałe wektory są przenoszone, aby umieścić je jeden po drugim.

Wektor F_R jest skierowany z pochodzenia F₁ do końca F₄. Jego wielkość wynosi 5.2 N i tworzy kąt 26.5 w odniesieniu do poziomego.

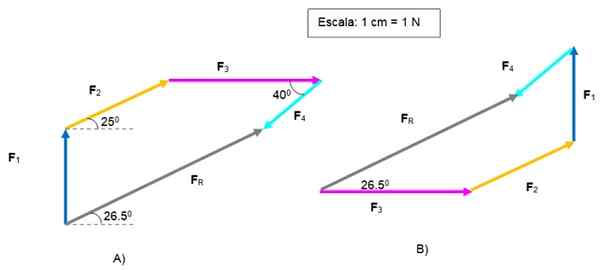Wektorowa suma graficzna. Źródło: f. Zapata.

Na rysunku B Ten sam problem został rozwiązany, zaczynając od F₃ i kończąc z F₄, Aby uzyskać to samo F_R .

Wielokąty są różne, ale wynik jest taki sam. Czytelnik może ponownie przetestować kolejność wektorów.

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill.
2. Bedford, 2000. DO. Mechanika inżynierii: statyczne. Addison Wesley.
3. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 1. Kinematyka. Pod redakcją Douglas Figueroa (USB).
4. Giambattista, a. 2010. Fizyka. 2. Wyd. McGraw Hill.
5. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1.