Przykłady metody metody równoległej, rozwiązane ćwiczenia

On Metoda równoległobramowa Jest to metoda graficzna dodawania dwóch wektorów w płaszczyźnie. Często jest używany do znalezienia wyniku dwóch sił nakładanych na ciało lub dwie prędkości, jak w przypadku pływaka, który zamierza przekroczyć rzekę prostopadle i jest kierowany przez prąd.

Aby zbudować równoległobok, początki wektorów, które należy dodać, narysowane na skalę, muszą się pokryć w punkcie.

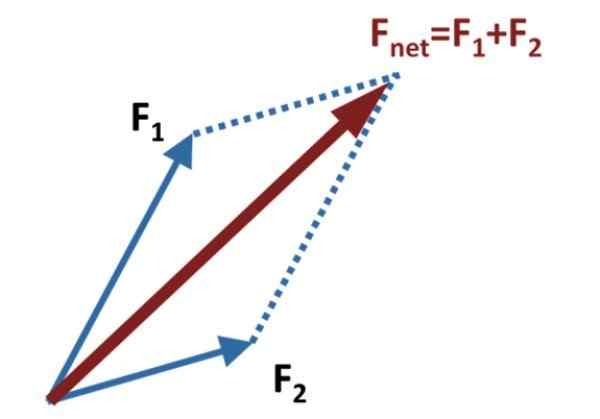
Rysunek 1. Metoda równoległoboku do dodania dwóch wektorów. Źródło: Wikimedia Commons.

Następnie linie pomocnicze są rysowane równolegle do każdego wektora, które docierają do końca drugiego, jak pokazano na górnej rysunku.

Dodatkowy lub wynikowy wektor, zwany również siłą netto, jest wektorem F_internet, to uzyskuje się przez rysowanie wektora, który wychodzi ze wspólnego pochodzenia F₁ I F₂, do punktu, w którym przecinają się pomocnicze linie równoległe. Na schemacie rysunku są one reprezentowane przez linie kropkowane.

Metoda odbiera swoją nazwę z figury utworzonej z uzależnionymi i linii pomocniczych, które są dokładnie równoległobokiem. Główną przekątną równoległoboku jest wektor sum.

Bardzo ważne jest, aby podkreślić, że kolejność, w której umieszczane są dodatkowe wektory, nie zmienia sum.

[TOC]

Przykład metody równoległoboku krok po kroku

Poniższy obraz pokazuje wektory v I Lub W arbitralnych jednostkach. Wektor v Mierzy 3.61 jednostek i tworzy kąt 56.3. z horyzontalnym, a Lub Środki 6.32 jednostki i kąt 18.4º w odniesieniu do tej linii odniesienia.

Może ci służyć: błąd losowy: wzór i równania, obliczenia, przykłady, ćwiczenia

Znajdźmy Twój wektor dodaje metodę równoległoboku.

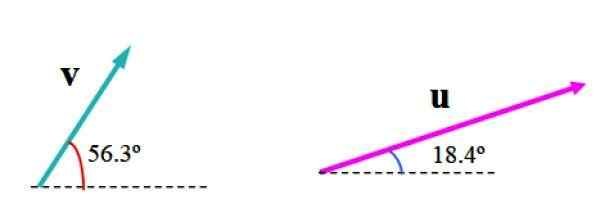Rysunek 2. Dowolne dwa wektory w płaszczyźnie, których chcemy znaleźć wynikowy wektor. Źródło: f. Zapata

Konieczne jest wybranie odpowiedniej skali, takiej jak ta pokazana na poniższym rysunku, na którym płaszczyzna została podzielona przez siatkę. Szerokość kwadratu reprezentuje jedną (1) jednostkę.

Ponieważ wektory nie zmieniają się podczas przenoszenia, są one umieszczane w taki sposób, aby ich pochodzenie pokryły się z pochodzeniem układu współrzędnych (obraz po lewej).

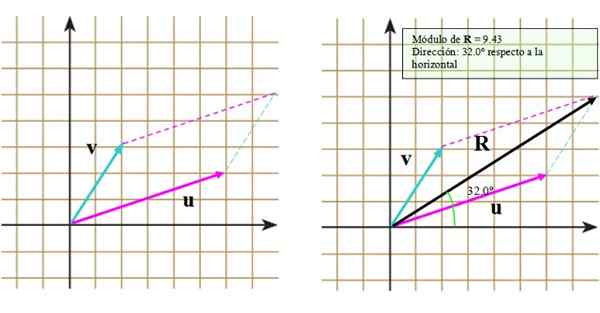Rysunek 3. Suma wektorów metodą równoległoboku. Źródło: f. Zapata.

Teraz wykonajmy te kroki:

1. Wektor koniec wektora v Linia segmentowa, która jest równoległa do wektora Lub.
2. Powtórz procedurę, ale tym razem z końcem wektora Lub.
3. Narysuj główną przekątną, która rozciąga się od wspólnego pochodzenia do punktu przecięcia linii segmentowych.

Wynik można zobaczyć na odpowiednim obrazie, na którym pojawia się wynikowy wektor R.

Jeśli chcemy poznać wielkość R, Możemy zmierzyć jego długość i porównać ją z skalą, którą mamy. A co do ich kierunku, osi pozioma lub oś pionowa może być używane na przykład jako odniesienia.

Za pomocą osi poziomej lub osi X, kąt R forma z tą osą jest mierzona za pomocą przenośnika i w ten sposób znamy adres R.

Również wielkość i kierunek R Można je obliczyć na podstawie twierdzeń cosinus i piersi, ponieważ utworzony równoległobok można podzielić na dwa przystające trójkąty, których boki to moduły wektorów Lub, v I R. Zobacz przykład rozwiązany 1.

Może ci służyć: szybkość natychmiastowa: definicja, wzór, obliczenia i ćwiczenia

Specjalny przypadek: suma wektorów prostopadłych

Gdy wektory są prostopadłe do siebie, uformowana figura jest prostokątem. Powstały moduł wektorowy odpowiada długości przekątnej, co można łatwo obliczyć za pomocą twierdzenia Pitagorasa.

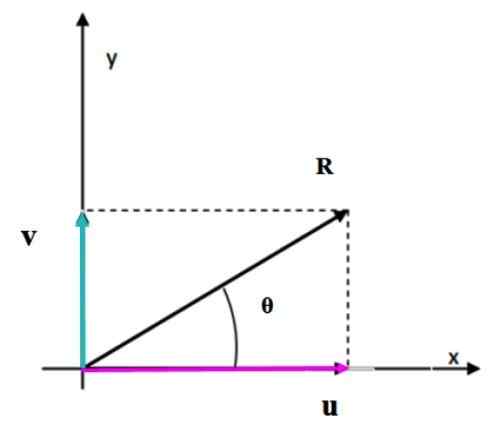Rysunek 4. Suma dwóch prostopadłych wektorów przy użyciu metody równoległoboku. Źródło: f. Zapata.

Rozwiązane ćwiczenia

- Ćwiczenie 1

Masz wektor v, który mierzy 3.61 jednostek i tworzy kąt 56.3. z poziomym i wektorem Lub, którego miara to 6.32 jednostki i tworzy kąt 18.4. (ryc. 2). Określ wynikowy moduł wektorowy R = Lub + v oraz kierunek, który tworzy wspomniany wektor z osą poziomą.

Rozwiązanie

Metodę równoległoboku jest stosowana zgodnie z opisanymi powyżej krokami, aby uzyskać wektor R. Jak wspomniano wcześniej, jeśli wektory są starannie narysowane po skali i za pomocą reguły i transportera, wielkości i kierunku R Są mierzone bezpośrednio na rysunku.

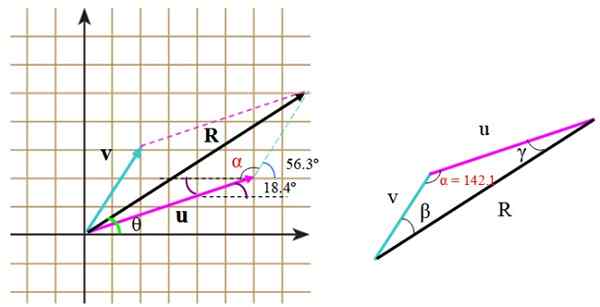Rysunek 5.- Obliczenie wielkości i kierunku powstałego wektora. Źródło: f. Zapata.

Można je również obliczyć bezpośrednio, za pomocą trygonometrii i właściwości kątów. Gdy utworzony trójkąt nie jest prostokątem, podobnie jak w tym przypadku, twierdzenie cosinusowe jest stosowane, aby znaleźć brakującą stronę.

W prawym trójkącie boki mierzą u, v i r. Aby zastosować twierdzenie cosinusowe, należy znać kąt między v I Lub, które możemy znaleźć za pomocą siatki, odpowiednio ustawiając kąty dostarczone przez oświadczenie.

Ten kąt jest α i składa się z:

α = (90-56.3.) + 90º +18.4. = 142.1st

Może ci służyć: czerwony krasnolud

Według twierdzenia Coseno:

R² = v² + Lub² - 2U⋅V⋅COS α = 3.61² + 6.32² - 23.61 × 6.32 × cos 142.1st = 88.98

R = 9.43 jednostki.

Wreszcie kąt między R A oś pozioma wynosi θ = 18.4 º + γ. Kąt γ można znaleźć na podstawie twierdzenia o piersi:

sin α / r = SEN γ / U

Dlatego:

sin γ = v (sin α / r) = 3.61 x (Sen 142.1st / 9.43)

γ = 13.6th

θ = 18.4 º + 13.6 º = 32º

- Ćwiczenie 2

Pływak przygotowuje się do przekroczenia rzeki pływających prostopadle do prądu o stałej prędkości 2.0 m/s. Pływak zaczyna od A, jednak kończy się w B, punkcie niższym, ze względu na prąd, który go odwrócił.

Jeśli prędkość prądu wynosi 0.8 m/s i wszystkie prędkości powinny znaleźć prędkość pływaka, co widziane przez obserwatora stojącego na brzegu.

Rozwiązanie

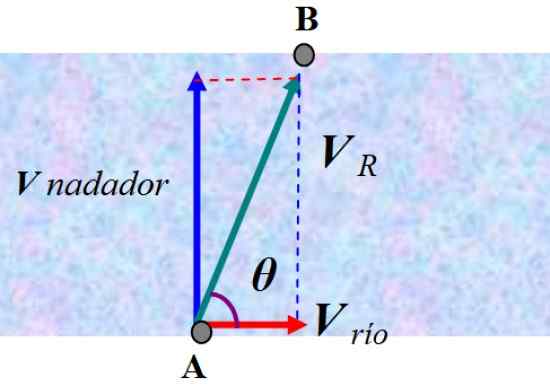Rysunek 6. Suma prędkości metodą równoległoboku. Źródło: f. Zapata.

Obserwator stojący na brzegu zobaczyłby, jak pływak jest kierowany zgodnie z wynikową prędkością V_R. Aby znaleźć odpowiedź, musimy dodać prędkość pływaka i prędkość prądu, którą nazywamy V _rzeka:

V _R = V _pływak + V _rzeka

Na rysunku, który nie jest na skali, wektory zostały dodane w celu uzyskania V _R. W takim przypadku można zastosować twierdzenie Pitagorasa w celu uzyskania jego wielkości:

V_R² = 2.0² + 0.8² = 4.64

V_R = 2.15 m/s

Adres, w którym pływak prostopadły jest łatwo obliczany, zauważając, że:

θ = ARCTG (2/0.8) = 68.2

Następnie pływak odbiega 90º - 68.2nd = 27.2. z oryginalnego adresu.

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill.
2. Bedford, 2000. DO. Mechanika inżynierii: statyczne. Addison Wesley.
3. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 1. Kinematyka. Pod redakcją Douglas Figueroa (USB).
4. Giambattista, a. 2010. Fizyka. 2. Wyd. McGraw Hill.
5. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1.