Suma historii Riemanna, formuły i nieruchomości, ćwiczenia

Riemann sum Jest to nazwa, która odbiera przybliżone obliczenie zdefiniowanej całki, za pomocą dyskretnej suma o skończonych warunkach. Wspólnym zastosowaniem jest podejście obszaru funkcji w grafice.

To niemiecki matematyk Georg Friedrich Bernhard Riemann (1826–1866) zaoferował po raz pierwszy rygorystyczną definicję całki funkcji w danym przedziale. Ogłosił to w artykule opublikowanym w 1854 roku. 

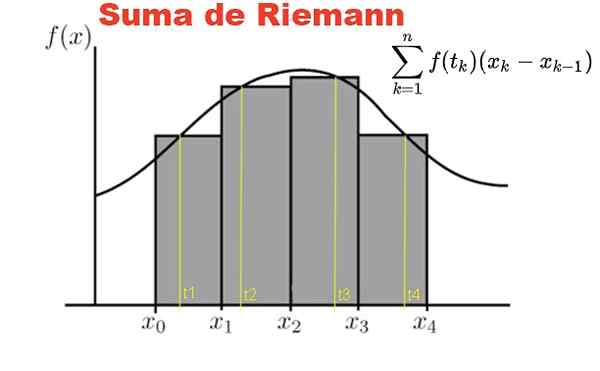
Rysunek 1. Suma Riemanna jest zdefiniowana na funkcji F i partycji w przedziale [x0, x1]. Źródło: Fanny Zapata.

Suma Riemanna jest zdefiniowana na funkcji y = f (x), przy czym x należy do zamkniętego przedziału [a, b]. W tym przedziale wykonano partycję P elementów n:

P = x₀= a, x₁, X₂,…, X_N= B

Oznacza to, że przedział jest podzielony w następujący sposób:

 Tutaj t_k jest między x_K-1 i x_k:

X_K-1 ≤ t_k ≤ x_k

Ryc. 1 pokazuje sumę riemann funkcji F w przedziale [x₀, X₄] Na partycji czterech podinterwali, szare prostokąty.

Suma reprezentuje całkowitą powierzchnię prostokątów, a wynik tej sumy jest numerycznie podejście do obszaru pod krzywą F, wśród odciętnych x = x₀ y x = x₄.

Oczywiście podejście do obszaru pod krzywą znacznie poprawia N partycji jest większy.  W ten sposób suma zbiega się do obszaru pod krzywą, gdy liczba N partycje mają tendencję do nieskończoności.

[TOC]

Formuły i właściwości

Suma F (x) Riemanna na partycji:

Może ci służyć: Rhomboid: Charakterystyka, jak wyjąć obwód i obszar

P = x₀= a, x₁, X₂,…, X_N= B

Zdefiniowane w przedziale [a, b], jest podany przez:

S (p, f) = ∑_{K = 1}^N f (t_k) (X_k - X_K-1) 

Gdzie t_k Jest to wartość w przedziale [x_k, X_K-1]. W sumie Riemanna zwykle stosuje się regularne odstępy szerokości ΔX = (B - a)/n, gdzie A i B są minimalnymi i maksymalnymi wartościami odciętej, podczas gdy N jest liczbą podziałów.

W takim przypadku Rysowa suma Riemanna Jest:

Sd (f, n) = [f (a+δx)+f (a+2Δx)+…+f (a+(n-1) δx)+f (b)]*δx

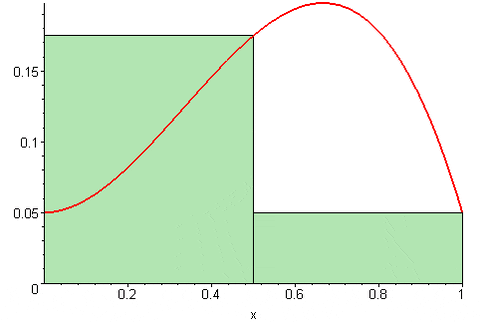Rysunek 2. Rysowa suma Riemanna. Źródło: Wikimedia Commons. 09GLASGOW09 [CC BY-SA (https: // creativeCommons.Org/licencje/by-sa/3.0)].

Podczas Riemanna pozostawiona suma Jest wyrażany jako:

Tak (f, n) = [f (a)+f (a+δx)+…+f (a+(n-1) δx)]*δx

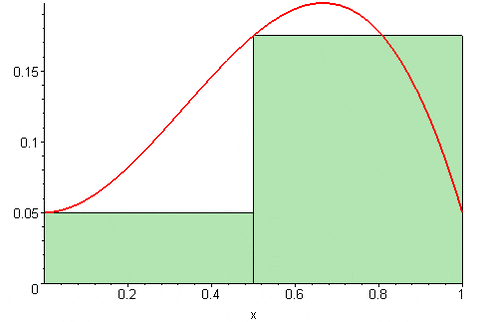Rysunek 3. Suma Riemanna opuściła. Źródło: Wikimedia Commons. 09GLASGOW09 [CC BY-SA (https: // creativeCommons.Org/licencje/by-sa/3.0)]

Wreszcie Riemann Central Sum Jest:

SC (F, N) = [F (A+δX/2)+F (A+3ΔX/2)+…+F (B-δx/2)]*δx

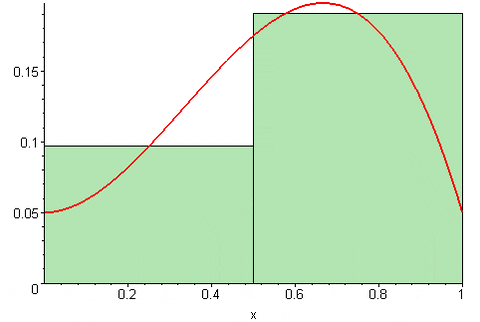Rysunek 4. Pośrednia suma Riemanna. Źródło: Wikimedia Commons. 09GLASGOW09 [CC BY-SA (https: // creativeCommons.Org/licencje/by-sa/3.0)]

W zależności od miejsca, w którym znajduje się punkt T_k W przedziale [x_k, X_K-1] Suma Riemanna może przecenić lub nie docenić dokładnej wartości obszaru pod krzywą funkcji y = f (x) (x). To znaczy prostokąty mogą wyróżniać się z krzywej lub być nieco poniżej tego.

Obszar pod krzywą

Główną właściwością sumy Riemanna i której staje się jego znaczenie, jest to, że jeśli liczba podziałów dąży do nieskończoności, wynik sumy zbiega się z zdefiniowaną całką funkcji:

Poprzednie wyrażenie odpowiada definicji całki Riemanna i ma zastosowanie, pod warunkiem, że funkcja F jest ciągła i miękka. Aby uzyskać bardziej szczegółowe funkcje, istnieją inne definicje całki (całka de standjes i integral de lebesgue).

Może ci służyć: standardowy błąd oceny: jak jest obliczany, przykłady, ćwiczenia

Rozwiązane ćwiczenia

- Ćwiczenie 1

Oblicz wartość całki zdefiniowanej między a = -2 do b = +2 funkcji:

f (x) = x²

Skorzystaj z suma Riemanna. Aby to zrobić, znajdź sumę regularnych partycji przedziału [a, b], a następnie weź limit matematyczny w przypadku, że liczba partycji przechowuje do nieskończoności. 

Rozwiązanie

To są kroki, którymi należy przestrzegać:

-Po pierwsze, interwał partycji jest definiowany jako: 

Δx = (B - a)/n. 

-Następnie suma Riemanna po prawej odpowiadającej funkcji f (x) jest taka:

-Teraz są one zastępowane a = -2 i b =+2, tak że interwał lub krok δx = 4/n. To znaczy, że suma Riemanna dla funkcji f (x) = x² Jest:

-Następnie rozwija się kwadratowy dwumian: 

[-2 +(4i/n)]² = 4 - (16 I /N) + (4 /n)² Siema²

-A następnie jest ostrożnie zastępowany w sumie:

-Następnym krokiem jest oddzielenie podsumowań i usunięcie stałych ilości jako wspólnego współczynnika każdej suma. Należy wziąć pod uwagę, że indeks to ja, a zatem liczby i warunki z N Są uważane za stałe:

-Każda suma jest oceniana, ponieważ dla każdego z nich istnieją odpowiednie wyrażenia. Na przykład pierwsze z podsumowań:

Drugi to:

 A trzeci to:

 -Zastępując wyniki podsumowań w sumie Riemanna, jest ostatecznie uzyskane:

S (f, n) = 16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²

-Na koniec musisz obliczyć całkę to:

= lim_N➝∞ [16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6N²] =

= 16 -(64/2) + (64/3) = 16/3 = 5,333

Czytelnik może sprawdzić, czy jest to dokładny wynik, który można uzyskać poprzez rozwiązanie całki nieokreślonej i ocenę granic integracji według reguły Barrow.

Może ci służyć: jak przekonwertować z km/h a m/s? Rozwiązane ćwiczenia

- Ćwiczenie 2

Określ w przybliżeniu obszar pod funkcją: 

f (x) = (1/√ (2π) e^(-X2/2)

Między x = -1 i x =+1, przy użyciu centralnej suma riemanna z 10 partycjami. Porównaj z dokładnym wynikiem i oszacuj różnicę procentową.

Rozwiązanie

Krok lub wzrost między dwiema kolejnymi wartościami dyskretnymi to:

ΔX = (1 - (-1)/10 = 0,2

Tak, że partycja P, na której zdefiniowane są prostokąty, była taka:

P = -1,0; -0,8; -0,6; -0,4; -0,2; 0,0; 0,2; 0,4; 0,6; 0,8; 1.0

Ale jak chcesz, jest suma centralna, funkcja f (x) zostanie oceniona w środkowych punktach podintervals, to znaczy w zestawie:

T = -0.9; -0,7; -0,5; -0,3; -0,1; 0,1; 0,3; 0,5; 0,7; 0,9.

Suma Riemanna (centralna) jest taka:

S = f (-0,9)*0,2 +f (-0,7)*0,2 +f (-0,5)*0,2 +… +f (0,7)*0,2 +f (0,9)*0,2

Ponieważ funkcja F jest symetryczna, możliwe jest zmniejszenie sumy do tylko 5 terminów, a wynik jest mnożony przez dwa:

S = 2*0,2*F (0,1)+ F (0,3)+ F (0,5)+ F (0,7)+ F (0,9)

S = 2*0,2*0,397+ 0,381+ 0,352+ 0,312+ 0,266 = 0,683

Funkcja podana w tym przykładzie jest nikt inny jak dobrze znany Bell Gaussa (znormalizowany, ze średnią równą zero i odchyleniem standardowym). Wiadomo, że obszar pod krzywą w przedziale [-1,1] dla tej funkcji wynosi 0,6827.

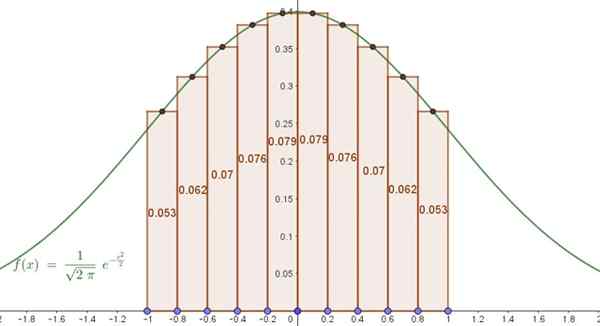Rysunek 5. Obszar pod przybliżonym dzwonkiem Gauss za pomocą suma Riemanna. Źródło: f. Zapata.

Oznacza to, że przybliżone rozwiązanie o zaledwie 10 terminach pokrywa się z dokładnym rozwiązaniem do trzech dziesiętnych. Błąd procentowy między przybliżoną całką a dokładnością wynosi 0,07%.

Bibliografia

1. Casteleiro, J. M., & Gómez-Alvarez, r. P. (2002). Kompleksowe obliczenia (ilustrowane ed.). Madryt: ESIC Editorial.
2. Unican. Historia koncepcji integralnej. Odzyskane z: repozytorium.Unican.Jest
3. UIS. Riemann Sums. Odzyskane z: matematyki.UIS.Edu.współ
4. Wikipedia. Riemann sum. Odzyskane z: jest.Wikipedia.com
5. Wikipedia. Integracja Riemanna. Odzyskane z: jest.Wikipedia.com