Suma wielomianów, jak się dzieje, przykłady, ćwiczenia

Suma wielomianów Jest to operacja, która polega na dodaniu dwóch lub więcej wielomianów, co skutkuje kolejnym wielomianem. Aby go wykonać, konieczne jest dodanie warunków tego samego rzędu każdego z wielomianów i wskazać wynikową sumę.

Najpierw krótko oceniamy znaczenie „warunków tego samego zamówienia”. Wielomian czyny składa się z sum i/lub odejmowania warunków.

Rysunek 1. Aby dodać dwa wielomiany, należy je zamówić, a następnie zmniejszyć podobne warunki. Źródło: Pixabay + Wikimedia Commons.

Warunki mogą być produktami o liczbach rzeczywistych i jednej lub więcej zmiennych, reprezentowanych na przykład z literami: 3x² i -√5.Do²pne³ Są warunkami.

Warunki tego samego zamówienia to te, które mają ten sam wykładnik lub moc, chociaż mogą mieć inny współczynnik.

-Warunki równej kolejności to: 5x³, √2 x³ i -1/2x³

-Różne zamówienia Warunki: -2x^-2, 2xy^-1 i √6x²I

Należy pamiętać, że można dodać lub odejmować tylko warunki tego samego zamówienia, operację znaną jako zmniejszenie. W przeciwnym razie suma jest po prostu wskazana.

Po wyjaśnieniu koncepcji terminów tego samego zamówienia, wielomiany są dodawane zgodnie z następującymi krokami:

-Zamówienie Najpierw wielomiany do dodania, wszystko w ten sam sposób, zwiększając lub zmniejszając, to znaczy z mocą od najmniejszej do największej lub odwrotnie.

-Ukończyć, W przypadku braku jakiejkolwiek mocy w sekwencji.

-Zmniejszyć Podobne warunki.

-Wskazać Wynikowa suma.

[TOC]

Przykłady sum wielomianowych

Zaczniemy od dodania dwóch wielomianów z jedną zmienną wywołaną X, na przykład wielomianki p (x) i q (x) podane przez:

P (x) = 2x² - 5x⁴ + 2x -x⁵ - 3x³ +12

Q (x) = x⁵- 25 x + x²

Zgodnie z opisanymi krokami zaczyna się od uporządkowania ich zmniejszania, co jest najbardziej typowym sposobem:

P (x) = -x⁵- 5x⁴  - 3x³  + 2x² + 2x +12

Może ci służyć: wpisany kąt koła: definicja, twierdzenia, przykłady

Q (x) = x⁵+ X² - 25x

Wielomianowa q (x) nie jest kompletna, widać, że moce z wykładnikiem 4, 3 i 0. Ten ostatni to po prostu niezależny termin, ten, który nie ma listu.

Q (x) = x⁵+ 0x⁴ + 0x³ + X² - 25x + 0

Po zakończeniu tego kroku są gotowe do dodania. Możesz dodać podobne warunki, a następnie wskazać sumę lub umieścić wielomiany uporządkowane przez siebie nawzajem i zmniejszyć kolumny, w ten sposób:

- X⁵ - 5x⁴  - 3x³ + 2x² + 2x +12

+ X⁵ + 0x⁴ + 0x³  +  X²  - 25x + 0     +

--

0x⁵-5x⁴ - 3x³  +3x² - 23x + 12 = p (x) + q (x)

Należy zauważyć, że po dodaniu, odbywa się to algebraicznie, szanując zasadę znaków, w ten sposób 2x + (-25 x) = -23x. To znaczy, jeśli współczynniki mają inny znak, a wynik przenosi znak głównego.

Dodaj dwa lub więcej wielomianów z więcej niż jedną zmienną

Jeśli chodzi o wielomiany z więcej niż jedną zmienną, jedna z nich jest wybierana, aby ją zamówić. Załóżmy na przykład, że należy dodać:

R (x, y) = 5x²  - 4y² +  8xy - 6y³ 

I:

T (x, y) = ½ x²- 6y²  - 11xy + x³I

Jedna ze zmiennych jest wybierana, na przykład x do kolejności:

R (x, y) = 5x² +  8xy - 6y³  - 4y²

T (x, y) = + x³y + ½ x² - 11xy - 6y² 

Brakujące warunki są natychmiast wypełnione, zgodnie z którym każdy wielomian ma:

R (x, y) = 0x³i + 5x² +  8xy - 6y³  - 4y²

T (x, y) = + x³y + ½ x² - 11xy + 0y³ - 6y² 

I oba są gotowe zmniejszyć podobne warunki:

0x³i + 5x² +  8xy - 6y³  - 4y²

Może ci służyć: współczynnik determinacji: wzory, obliczenia, interpretacja, przykłady

+ X³y + ½ x² - 11xy + 0y³ - 6y²       +

-

+ X³Y + 11/2x² - 3xy - 6y³  - 10Y²    = R (x, y) + t (x, y)

Ćwiczenia wielomianowe

- Ćwiczenie 1

W następnej sumie wielomianów wskazuj termin, który musi przejść w pustym miejscu, aby uzyskać sumę wielomianową:

-5x⁴  + 0x³ +  2x²         + 1

X⁵  + 2x⁴             - 21x² + 8x - 3

2x⁵             +9x³             -14x

-

-6x⁵+10x⁴ -0x³  + 5x²   - 11x + 21

Rozwiązanie

Aby uzyskać -6x⁵ Wymagany jest termin formularza AX⁵, tak, że:

A + 1+ 2 = -6

Dlatego:

A = -6-1-2 = -9

A poszukiwany termin jest:

-9x⁵

-Kontynuuj w podobny sposób, aby znaleźć resztę warunków. Oto wykładnik 4:

-5 + 2 + A = 10 → A = 10 + 5-2 = 13

Brakujący termin to: 13x⁴.

-Dla x mocy³ Natychmiast jest to, że termin ten musi wynosić -9x³, W ten sposób współczynnik terminu sześciennego wynosi 0.

-Jeśli chodzi o moce kwadratowe: a + 8-14 = -11 → a = -11 -8 + 14 = -5, a termin to -5x².

-Termin liniowy jest uzyskiwany przez +8 -14 = -11 → A = -11 + 14 -8 = -5, będąc brakującym terminem -5x.

-Wreszcie niezależny termin wynosi: 1-3 + A = -21 → A = -19.

- Ćwiczenie 2

Płaski teren jest otoczony, jak pokazano na rysunku. Znajdź wyrażenie dla:

a) Obwód i

b) jego obszar, pod względem wskazanych długości:

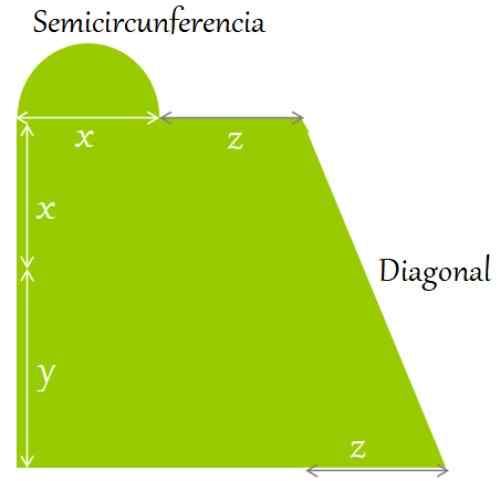Rysunek 2. Płaski teren jest otoczony wskazanymi formą i wymiarami. Źródło: f. Zapata.

Rozwiązanie

Obwód jest zdefiniowany jako suma boków i konturów rysunku. Zaczynając w lewym dolnym rogu, w kierunku dłoni zegara, masz:

Może ci służyć: Isosceles Trapezoid: właściwości, relacje i wzory, przykłady

Obwód = y + x + długość półkola + z + długość po przekątnej + Z + z + x

Półkola ma średnicę równą x. Ponieważ promień ma połowę średnicy, musi:

Radio = x/2.

Formuła długości całkowitego obwodu jest:

L = 2π x radio

Więc:

Długość półkola = ½. 2π (x/2) = πx/2

Ze swojej części przekątna jest obliczana z twierdzeniem Pitagoras stosowanym na boki: (x+y), która jest pionową stroną i z, która jest pozioma:

Diagonal = [(x+y)² + z²]^1/2

Wyrażenia te są zastępowane na obwodzie, aby uzyskać:

Obwód = y + x + πx/2 + z + [(x + y)² + z²]^1/2+ Z + X + Z

Podobne warunki są zmniejszone, ponieważ suma wymaga uproszczenia wyniku do maksimum:

Obwód = y + [x + π (x/2) + x] + z + z + z + [(x + y)² + z²]^1/2 = y + (2 + π /2) x + 3z

Rozwiązanie b

Powstały obszar to suma obszaru prostokąta, półkola i prawy trójkąt. Formuły tych obszarów to:

-Prostokąt: Podstawa X Wysokość

-Półkole: ½ π (radio)²

-Trójkąt: Podstawa x wysokość /2

Obszar prostokąta

(x+y). (x+z) = x² + Xz + yx + yz

Obszar półkola

½ π (x/2)² = π x² / 8

Obszar trójkąta

½ z (x + y) = ½ zx + ½ zy

Całkowita powierzchnia

Aby znaleźć całkowitą powierzchnię, dodane są wyrażenia dla każdego obszaru częściowego:

Całkowity obszar = x² + Xz + yx + yz + (π x² / 8) + ½ ZX + ½ Zy

I wreszcie wszystkie podobne terminy:

Całkowity obszar = (1 + π/8) x² + 3/2 xy + 3/2yz + yx

Bibliografia

1. Baldor, a. 1991. Algebra. Wenezuelskie redakcje kulturalne.DO.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Matematyka jest zabawna. Dodanie i odejmowanie wielomianów. Odzyskany z: MathSisfun.com.
4. Monterey Institute. Dodawanie i odejmowanie wielomianów. Odzyskane z: Montereyinstitute.org.
5. UC Berkeley. Algebra wielomianów. Odzyskane z: matematyki.Berkeley.Edu.