System ósemkowy

Co to jest system ósemkowy?

On System ósemkowy Jest to podstawowy system numeracji osiem (8); To znaczy składa się z ośmiu cyfr, które to: 0, 1, 2, 3, 4, 5, 6 i 7. Dlatego każda cyfra liczby ósemkowej może mieć dowolną wartość od 0 do 7. Liczby ósemkowe powstają z liczb binarnych.

Jest tak, ponieważ jego podstawa jest dokładną mocą dwóch (2). Oznacza to, że liczby należące do systemu ósemkowego powstają, gdy są zgrupowane w trzy kolejne cyfry, uporządkowane od prawej do lewej, w ten sposób uzyskując swoją wartość dziesiętną.

Historia systemu ósemkowego

System ośmiokadowy ma swoje pochodzenie w czasach starożytnych, kiedy ludzie używali rąk do liczenia ośmiu przez osiem zwierząt.

Na przykład, aby policzyć liczbę krów w stajni, prawa ręka zaczęła mieć kciuk z małym palcem; Następnie, by policzyć drugie zwierzę, kciuk zniknął z palcem wskazującym i tak dalej z pozostałymi palcami każdej ręki, aż do ukończenia 8.

Istnieje możliwość, że system numeracji ósemkowej przed dziesiętnym, aby móc policzyć przestrzenie międzydigitalne; to znaczy, powiedz wszystkie palce, z wyjątkiem kciuków.

Następnie ustanowiono system numeracji ósemkowej, który powstał z systemu binarnego, ponieważ potrzebuje wielu cyfr, aby reprezentować tylko jedną liczbę; Odtąd utworzono systemy ośmiokrotne i sześciokątne, które nie wymagają tak wielu cyfr i które mogą łatwo przekonwertować na system binarny.

System numeracji ósemkowej

System ósemkowy składa się z ośmiu cyfr od 0 do 7. Mają one taką samą wartość jak w przypadku systemu dziesiętnego, ale ich względna wartość zmienia się w zależności od pozycji. Wartość każdej pozycji jest podana przez moce podstawowe 8.

Może ci służyć: reguła t: Charakterystyka, tak że jest przykłady

Pozycje cyfr w numerze ósemkowym mają następujące pesos:

8⁴, 8³, 8², 8¹, 8⁰, Point Octal, 8^-1, 8^-2, 8^-3, 8^-4, 8^-5.

Główna cyfra ośmiorodosła to 7; W ten sposób, gdy liczy się w tym systemie, rośnie pozycja cyfry od 0 do 7. Po osiągnięciu 7 jest poddawany recyklingowi na 0 dla następnej liczby; Zwiększa to następującą pozycję cyfrową. Na przykład, aby zliczyć sekwencje, w systemie ósemkowym będzie:

• 0, 1, 2, 3, 4, 5, 6, 7, 10.
• 53, 54, 55, 56, 57, 60.
• 375, 376, 377, 400.

Istnieje fundamentalne twierdzenie, które jest stosowane do systemu ósemkowego i jest wyrażane w następujący sposób:

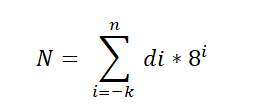
W tym wyrażeniu DI reprezentuje cyfrę pomnożoną przez zasadę zasadą 8, która wskazuje wartość pozycyjną każdej cyfry, w taki sam sposób, w jaki jest zamówiony w układzie dziesiętnym.

Na przykład masz numer 543.2. Aby zabrać go do systemu ósemkowego, rozkłada się w następujący sposób:

N = ∑ [(5 _* 8²) + (4 _* 8¹) + (3 _*8⁰) + (2 _*8^-1)] = (5 * 64) + (4 * 8) + (2 * 1) + (2 * 0,125)

N = 320 +32 + 2 + 0,25 = 354 + 0,25_D

W ten sposób masz 543,2_Q = 354,25_D. Klopa dolna wskazująca, że ​​jest to liczba ósemkowa, która może być również reprezentowana przez numer 8; a indeks dolny D odnosi się do liczby dziesiętnej, którą można również przedstawić za pomocą numeru 10.

Konwersja układu ósemkowego na dziesiętne

Aby przekonwertować numer układu ósemkowego na jego równoważny w układ dziesiętny, każda cyfra osławiona musi zostać pomnożona przez jego wartość pozycyjną, zaczynając od prawej.

Przykład 1

732₈ = (7_* 8²) + (3_* 8¹) + (2_* 8⁰) = (7 _* 64) + (3 _* 8) + (2 _* 1)

732₈= 448 +24 +2

732₈= 474₁₀

Może ci służyć: równość matematyczna

Przykład 2

26,9₈ = (2 _*8¹) + (6_* 8⁰) + (9_* 8^-1) = (2 _* 8) + (6 _* 1) + (9 _* 0,125)

26,9₈ = 16 + 6 + 1.125

26,9₈= 23 125₁₀

Konwersja układu dziesiętnego na ósemkę

Liczbę dziesiętną można przekształcić w liczbę ósemkową przy użyciu metody powtarzanego podziału, w której liczba całkowita dziesiętna jest podzielona przez 8, aż iloraz będzie równy 0, a marnotrawstwo każdego podziału będą reprezentować numer ośmiorodowy.

Odpady są uporządkowane od ostatniego do pierwszego; Oznacza to, że pierwsza pozostałość będzie najmniej znaczącą cyfrą liczby ósemkowej. W ten sposób najważniejszą cyfrą będzie ostatnia pozostałość.

Przykład

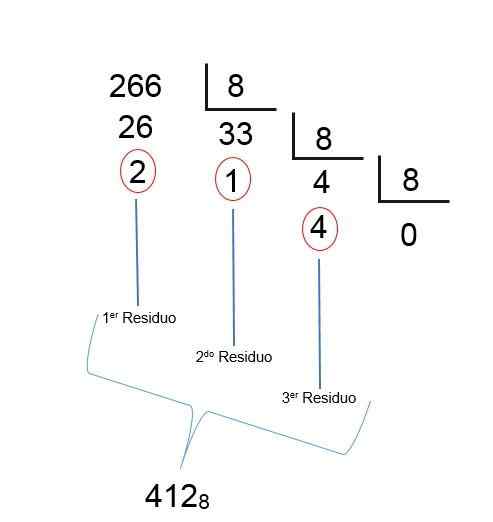
Oktal dziesiętnego numeru 266₁₀

- Numer dziesiętny 266 jest podzielony przez 8 = 266/8 = 33 + 2 pozostałości.

- Następnie 33 jest podzielone przez 8 = 33/8 = 4 + 1 pozostałość.

- 4 jest podzielone przez 8 = 4/8 = 0 + 4 reszty.

Podobnie jak w przypadku ostatniego podziału, uzyskano iloraz mniejszy niż 1, oznacza to, że wynik został znaleziony; Tylko pozostałości muszą być zamówione na odwrót, tak że liczba ósemkowa dziesiętna 266 wynosi 412, jak widać na następującym obrazie:

Konwersja systemu binarnego

Przekształcenie układu ósemkowego na binarne odbywa się podczas konwersji cyfry ósemkowej w jej równoważną cyfrę binarną, utworzoną przez trzy cyfry. Istnieje tabela pokazująca, jak stały się osiem możliwych cyfr:

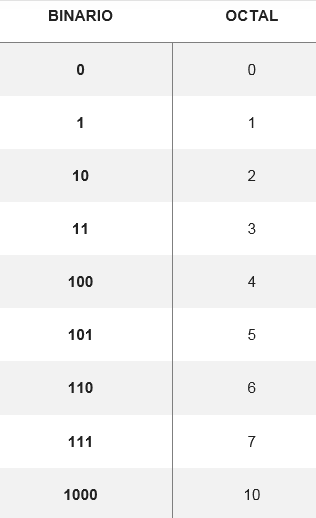
Na podstawie tych konwersji możesz zmienić dowolną liczbę systemu ósemkowego na binarny, na przykład przekonwertowanie numeru 572₈ Twoje odpowiedniki są poszukiwane w tabeli. Zatem musisz:

5₈ = 101

7₈= 111

2₈ = 10

Dlatego 572₈ równoważny w układzie binarnym do 10111110.

Układ binarny do konwersji ósemkowej

Proces konwersji liczb całkowych na liczby całkowitych ósemek jest odwrotnym działaniem do poprzedniego procesu.

Może ci służyć: jakie są elementy kąta?

To znaczy bity liczb binarnych są pogrupowane w dwie grupy trzech bitów, zaczynając od prawej do lewej. Następnie konwersja binarna do ósemka wykonuje się z poprzednią tabelą.

W niektórych przypadkach liczba binarna nie będzie miała grup 3 bitów; Aby go ukończyć, jedno lub dwie zera są dodawane na lewo od pierwszej grupy.

Na przykład, aby zmienić liczbę binarną 11010110 na ósemkę, wykonano następujące:

- Grupy 3 bitów są tworzone po prawej stronie (ostatni bit):

11010110

- Ponieważ pierwsza grupa jest niekompletna, po lewej stronie dodaje się zero:

011010110

- Konwersja jest wykonana z tabeli:

011 = 3

010 = 2

110 = 6

W ten sposób liczba binarna 011010110 jest równoważna 326₈.

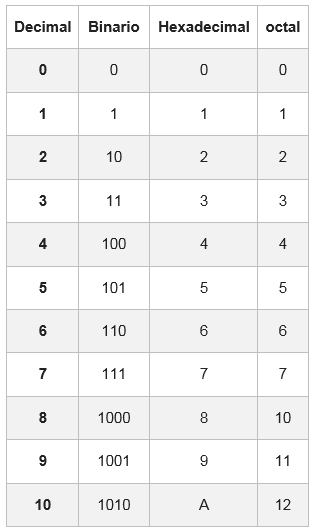
Konwersja systemu ósemkowego na szesnastkowe i odwrotnie

Aby zmienić liczbę ósemkę na system sześciokadciowy lub sześciokadcicowy, konieczne jest, aby liczba ta była najpierw binarna, a następnie na pożądany system.

W tym celu istnieje tabela, w której każda cyfra sześciokadciowca jest reprezentowana z jego równoważnością w układzie binarnym, złożonym z czterech cyfr.

W niektórych przypadkach liczba binarna nie będzie miała grup 4 bitów; Aby go ukończyć, jedno lub dwie zera są dodawane na lewo od pierwszej grupy

Przykład

Konwertuj liczbę ósemkę 1646 na numer szesnastkowy:

- Liczba binarna do ósemek do

1₈ = 1

6₈ = 110

4₈ = 100

6₈ = 110

- Tak więc 1646₈ = 1110100110.

- Aby przekształcić się z binarnego na sześciokadcicę, są pierwsi zamówione w grupie 4 bitów, zaczynając od prawej do lewej:

11 1010 0110

- Pierwsza grupa jest zakończona zerami, aby mogła mieć 4 bity:

0011 1010 0110

- Dokonuje się konwersji szesnastkowej systemu binarnego. Równoważniki są zastępowane za pomocą tabeli:

0011 = 3

1010 = a

0110 = 6

W ten sposób liczba ósemkowa 1646 jest równoważna 3A6 w układzie szesnastkowym.