Centralne właściwości symetrii, przykłady i ćwiczenia

Dwa punkty a i „mają Symetria centralna dotyczące punktu lub gdy segment AA „przechodzi przez niego i jest również punktem środkowym AA”. Do punktu lub nazywa się Centrum symetrii.

Centralna symetryczna trójkąta ABC w odniesieniu do jednego punktu lub, jest inny trójkąt a'b'c ', który ma następujące cechy:

-Homologiczne segmenty są równa długość 

-Ich odpowiednie kąty mają tę samą miarę.

Rysunek 1. ABC Triangle i jego symetryczny a'b'c '. Źródło: f. Zapata.

Na rycinie 1 trójkąt ABC (czerwony) i jego centralny symetryczny a'b'c '(zielony), w odniesieniu do środka symetrii lub. 

Na tej samej figurze uważny obserwator zdałby sobie sprawę, że ten sam wynik uzyskuje się poprzez zastosowanie oryginalnego obrotu trójkąta, o ile jest to 180º i skupione na lub skupionym na lub.

Dlatego centralna symetria jest równoważna zwrotowi 180º w odniesieniu do środka symetrii.

[TOC]

Właściwości centralnej symetrii

Centralna symetria ma następujące właściwości:

-Centrum symetrii jest punktem środkowym segmentu, który łączy punkt z jego symetrycznym.

-Symetryczny punkt innego, który znajduje się w centrum symetrii, pokrywa się z centrum symetrii.

-Centralna symetryczna trójkąta to przystający trójkąt (równy) do oryginału.

-Obraz za pomocą centralnej symetrii obwodu jest kolejnym obwodem równego promienia.

-Krąg ma centralną symetrię w odniesieniu do własnego centrum.

Rysunek 2. Projekt z centralną symetrią. Źródło: Pixabay.

-Elipsa ma centralną symetrię w odniesieniu do swojego centrum.

-Segment ma centralną symetrię w odniesieniu do punktu środkowego.

-Trójkąt równoboczny nie ma centralnej symetrii w odniesieniu do jego centrum, ponieważ jego symetryczne, choć przystające dla pierwszego, daje równoboczny trójkąt.

Może ci służyć: y = 3sen (4x) Okres funkcji

-Squares mają centralną symetrię w odniesieniu do swojego centrum.

-Pentagonowi brakuje centralnej symetrii w odniesieniu do centrum.

-Regularne wielokąty mają centralną symetrię, gdy mają wiele stron momentu obrotowego.

Przykłady

Kryteria symetrii mają wiele zastosowań w nauce i inżynierii. Centralna symetria jest obecna w naturze, na przykład kryształy lodu i pajęczyny mają tego rodzaju symetrię.

Ponadto wiele problemów można łatwo rozwiązać, gdy stosuje się istnienie centralnej symetrii i innych rodzajów symetrii. Dlatego wygodne jest szybko identyfikować.

Rysunek 3. Kryształy lodu mają centralną symetrię. Źródło: Pixabay.

Przykład 1

Biorąc pod uwagę punkt P współrzędnych (a, b), musisz znaleźć współrzędne jego symetrycznego p 'dotyczące pochodzenia lub współrzędnych (0, 0).

Pierwszą rzeczą jest zbudowanie p 'p', dla którego rysowana jest linia, która przechodzi przez pochodzenie lub i przez punkt p. Równanie tej linii to y = (b/a) x.

Teraz zadzwoń (a ', b') współrzędne punktu symetrycznego p '. Punkt p. Ponadto odległość OP musi być równa OP ”, która analitycznie pisze w ten sposób:

(A² + B²) = √ (a '² + B '² )

Poniżej wymieni B '= [(b/a).A '] w poprzednim wyrażeniu i kwadrat po obu stronach równości w celu wyeliminowania korzenia kwadratowego: (a² + B²) = [a '² + (B²/Do²).Do'²]

Wyodrębniając wspólny czynnik i upraszczanie, jest on osiągany² = a². To równanie ma dwa rzeczywiste rozwiązania: a '= +a lub a' = -a. 

Aby uzyskać B ', używamy ponownie B' = (b/a) a '. Jeśli dodatnie rozwiązanie A jest zastąpione, osiąga się, że B '= B. A po wymianie roztworu ujemnego, wówczas B '= -B. 

Może ci służyć: jakie są 7 elementów obwodu?

Pozytywne rozwiązanie daje P 'ten sam punkt P, więc jest wykluczone. Negatywne rozwiązanie zdecydowanie oferuje współrzędne punktu symetrycznego:

P ': (-a, -b)

Przykład 2

Należy wykazać, że segment AB i jego symetryczny centralny A'B „mają taką samą długość.

Zaczynając od współrzędnych punktu A, które są (ax, ay) i te punktu B: (bx, przez), długość AB jest podana przez:

D (ab) = √ ((bx - ax)² + (Przez - ay)² )

Analogicznie segment symetryczny a'b 'będzie miał długość podaną przez:

d (a'b ') = √ ((bx' - ax ')² + (Przez „ - ay”)² )

Współrzędne punktu symetrycznego A „są ax” = -ax i ay '= -Ay. Podobnie te z B 'są bx' = -Bx i przez '= -By. Jeśli te współrzędne zostaną zastąpione w równaniu odległości d (a'b '), masz:

D (a'b ') = √ ((-Bx + ax)² + (-By + ay)²) Jest to równoważne:

 √ ((bx - ax)² + (Przez - ay)²) = D (AB)

Wykazane, że oba segmenty mają tę samą długość.

Rozwiązane ćwiczenia

- Ćwiczenie 1

W analitycznym sposób wykazać, że centralny symetryczny lub okrąg o promieniu r i środku lub, jest tym samym oryginalnym obwodem.

Rozwiązanie

Równanie promienia R i środkowego okręgu (0,0) wynosi:

X² + I² = R² (Równanie obwodu c)

Jeżeli w każdym punkcie P obwodu i współrzędnych (x, y) stwierdzono jego symetryczną współrzędną p '), równanie obwodu symetrycznego wynosi:

X '² + I'² = R² (Równanie obwodu symetrycznego C ')

Teraz odnosimy się do wyniku przykładu 1, który stwierdza, że ​​współrzędne punktu P ', symetryczne do P i współrzędnych (a, b), to (-a, -b). 

Ale w tym ćwiczeniu punkt P ma współrzędne (x, y), więc jego symetryczny p 'będzie miał współrzędne x' = -x e y '= -y. Zastąpienie tego w równaniu obwodu symetrycznego to:

Może ci służyć: Rhomboid: Charakterystyka, jak wyjąć obwód i obszar

(-X)² + (-I)² = R²

Co jest równoważne: x²+ I² = R², stwierdzenie, że centralna symetryczna symetryka koła w odniesieniu do jego centrum jest sam obwód.

- Ćwiczenie 2

W geometryczny sposób wykazania, że ​​centralna symetria zachowuje kąty.

Rozwiązanie

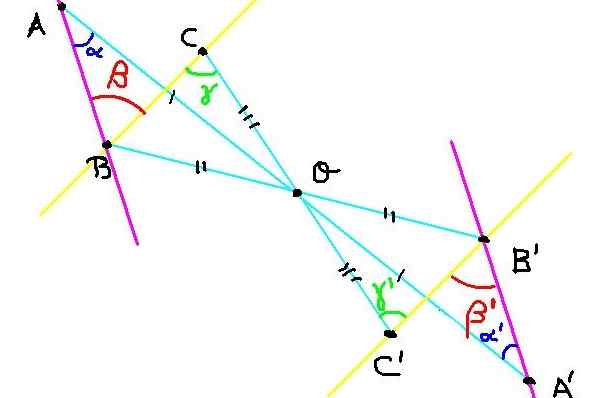Rysunek 4. Budowa punktów symetrycznych do ćwiczeń 2. Źródło: f. Zapata.

W samolocie są trzy punkty A, B i C. Jego symetryczne A ', B' i C 'są zbudowane w odniesieniu do środka symetrii lub, jak pokazano na rycinie 4. 

Teraz musimy wykazać, że kąt ∡Abc = β ma taką samą miarę jak kąt ∡a'b'c '= β' '.

Ponieważ C i C 'są symetryczne, wówczas OC = OC'. Podobnie ob = ob 'y oa = oa'. Z drugiej strony kąt ∡Boc = ∡B'oc 'za przeciwstawienie się wierzchołkowi.

Wówczas trójkąty Boc i B'oc 'są zgodne z tym, że mają równy kąt między dwiema stronami.

Ponieważ BOC jest zgodny z B'oc, wtedy kąty  γ I γ ' Są równe. Ale te kąty, oprócz satysfakcji γ = γ ' Są wewnętrzne na naprzemienne linie BC i B'C, co oznacza, że ​​linia BC jest równoległa do B'C '.

Podobnie baa jest zgodny z b'oa 'tego, co jest następujące α = α ' . Ale  α I α ' Są to wewnętrzne alternatywne kąty między liniami BA i B'a, o których stwierdzono, że linia BA jest równoległa do b'a ”.

Ponieważ kąt ∡ABC = β ma swoje równoległe strony z kątem ∡a'b'c '= β', a także oba są ostre, stwierdza się, że:

∡ABC = ∡A'B'C '= β = β' '

W ten sposób, że centralna symetria zachowuje miarę kątów.

Bibliografia

1. Baldor, J. DO. 1973.Płaska i przestrzeń geometria. Cultural American Cultural. 
2. Prawa i formuły matematyczne. Systemy pomiaru kąta. Pobrano z: Ingemecanica.com.
3. Wentworth, G. Geometria planety. Odzyskane z: Gutenberg.org.
4. Wikipedia. Symetria centralna. Odzyskane z: jest.Wikipedia.com
5. Wikipedia. Przenośnik. Odzyskane z: jest.Wikipedia.com
6. Zapata f. Wewnętrzne i zewnętrzne kąty koniugatu. Pobrano z: Lifer.com