Uzupełniające się kąty, które i jak obliczane są przykłady, ćwiczenia

Dwa lub więcej kąty to Kąty komplementarne Jeśli suma jego miar odpowiada sumie kątu prostego. Jak wiadomo, miara prostego kąta w stopniach wynosi 90º, a w radiach wynosi π/2.

Na przykład dwa kąty przylegające do przeciwprostokątnej trójkąta prostokąta są dla siebie komplementarne, ponieważ suma ich miar wynosi 90º. Poniższa liczba jest bardzo ilustracyjna:

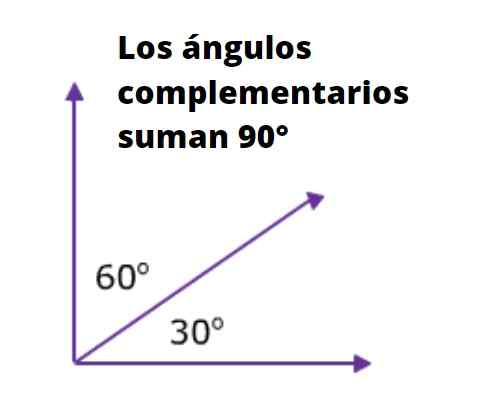
Rysunek 1. Po lewej stronie kilka kątów ze wspólnym wierzchołkiem. Po prawej kąt 60º, który uzupełnia kąt α (alfa). Źródło: f. Zapata.

Rycina 1 pokazuje w sumie cztery kąty. α i β są komplementarne, ponieważ są przylegający i jego pełna suma prostego kąt. Podobnie β jest uzupełniający się do γ, gdzie wynika z tego, że γ i α są tak samo.

Teraz, ponieważ suma α i δ jest równa 90 stopni, można powiedzieć, że α i δ są komplementarne. Ponadto, ponieważ β i δ mają ten sam komplementarny α, można powiedzieć, że β i δ mają tę samą miarę.

 [TOC]

Przykłady kątów uzupełniających

W poniższych przykładach należy znaleźć nieznane kąty, wskazane z przesłuchaniem na rycinie 2.

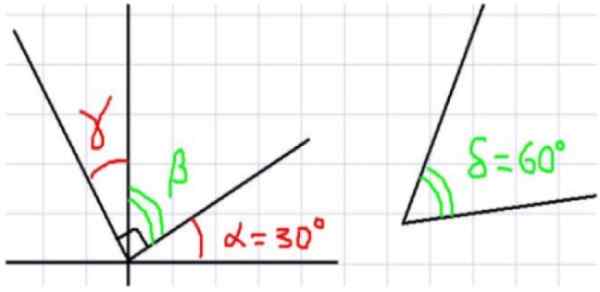
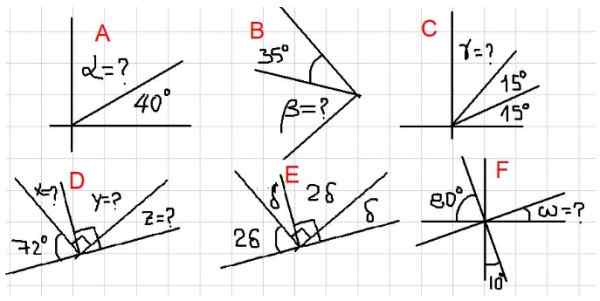Rysunek 2. Różne przykłady kątów uzupełniających. Źródło: f. Zapata.

- Przykłady A, B i C

Poniższe przykłady są w kolejności złożoności.

Przykład a

Na górnej figurze mamy, że sąsiednie kąty α i 40º sumują się pod kątem prostym. To jest α + 40º = 90º, a zatem α = 90º-40º = 50º.

Przykład b

Ponieważ β jest uzupełniający się z kątem 35º, wówczas β = 90º - 35º = 55º.

Może ci służyć: ortoedro: wzory, obszar, objętość, przekątna, przykłady

Przykład c

Z ryc. 2C suma γ + 15º + 15º = 90º. To znaczy, że γ jest uzupełniający do kąta 30 = 15º + 15º. Aby:

γ = 90º- 30º = 60º

- Przykłady d, e i f

W tych przykładach w grę wchodzi więcej kąty. Aby znaleźć niewiadomy, czytelnik musi zastosować pojęcie kąt uzupełniającego tyle razy, ile to konieczne.

Przykład d

Ponieważ x jest uzupełniający się z 72º, wynika z tego, że x = 90º - 72º = 18º. Ponadto i jest uzupełniający się z x, a następnie y = 90º - 18º = 72º.

Wreszcie Z jest uzupełniający się i. Z wszystkich powyższych wynika, że:

Z = 90º - 72º = 18º

Przykład e

Kąty δ i 2δ są uzupełniające się, a zatem δ + 2δ = 90º.

To jest 3Δ = 90º, co oznacza, że ​​δ = 90º / 3 = 30º.

Przykład f

Jeśli nazwiemy kąt między ω a kątem 10, trzeba było go uzupełnić, ponieważ zaobserwowano, że ich pełna suma kąt. Gdzie następuje, że u = 80º. Ponieważ u jest uzupełniające się z ω, a następnie ω = 10º.

Ćwiczenia

Poniżej zaproponowano trzy ćwiczenia. We wszystkich z nich wartość kątów a i b należy znaleźć w stopniach, aby relacje pokazane na rycinie 3 są spełnione.

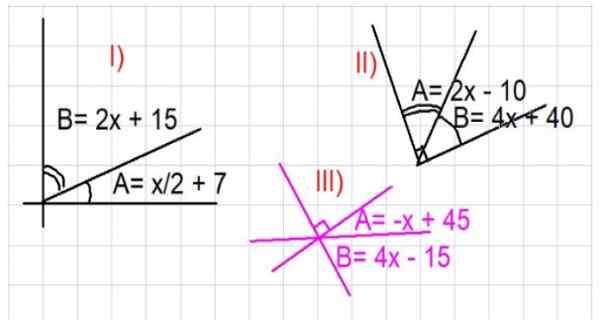Rysunek 3. Ilustracje kątów uzupełniających. Źródło: f. Zapata.

- Ćwiczenie 1

Określ wartości kątów A i B części I) na rycinie 3.

Rozwiązanie

Z pokazanego rysunku widać, że A i B są uzupełniające się, a zatem A + B = 90º. Ekspresja A i B jest zastępowana jako funkcja x podana w części I):

Może ci służyć: Radio zbieżności: definicja, przykłady i ćwiczenia rozwiązane

(x/2 + 7) + (2x + 15) = 90

Następnie warunki są odpowiednio zgrupowane i uzyskuje się proste równanie liniowe:

(5x/2) + 22 = 90

Odejmowanie 22 u obu członków to:

5x/2 = 90 -22 = 68

I wreszcie wartość x jest oczyszczona:

x = 2*68/5 = 136/5

Teraz kąt jest zastępujący wartość x:

A = (136/5)/2 +7 = 103/5 = 20,6 º.

Podczas gdy kąt B to:

B = 2*136/5 + 15 = 347/5º = 69,4º .

- Ćwiczenie 2

Znajdź wartości kąty A i B obrazu II, ryc. 3.

Rozwiązanie

Ponownie, ponieważ A i B są kątami uzupełniającymi, musisz: A + B = 90º. Zastąpienie wyrażenia A i B jako funkcji x podanej w części II) na rycinie 3 to:

(2x - 10) + (4x +40) = 90

Podobne terminy są zgrupowane w celu uzyskania równania:

6 x + 30 = 90

Uzyskuje się dzielenie obu członków między 6:

x + 5 = 15

Gdzie następuje, że x = 10º.

Dlatego:

A = 2*10 - 10 = 10º

B = 4*10 + 40 = 80º.

- Ćwiczenie 3

Określ wartości kątów A i B części III) na rycinie 3.

Rozwiązanie

Liczba jest starannie analizowana w celu poszukiwania kątów uzupełniających. W takim przypadku musisz + b = 90 stopni. Zastępując wyrażenie A i B jako funkcję x podaną na rysunku, masz:

(-X +45) + (4x -15) = 90

3 x + 30 = 90

Dzielenie obu członków przez 3 jest następująco:

x + 10 = 30

Gdzie następuje, że x = 20º.

To znaczy, że kąt a = -20 +45 = 25º. A dla swojej części: B = 4*20-15 = 65º.

Kąty prostopadłe

Mówi się, że są dwa kąty strony prostopadłe Jeśli każda strona ma odpowiednią prostopadłą w drugim. Poniższa liczba wyjaśnia koncepcję:

Może ci służyć: sukcesja złożona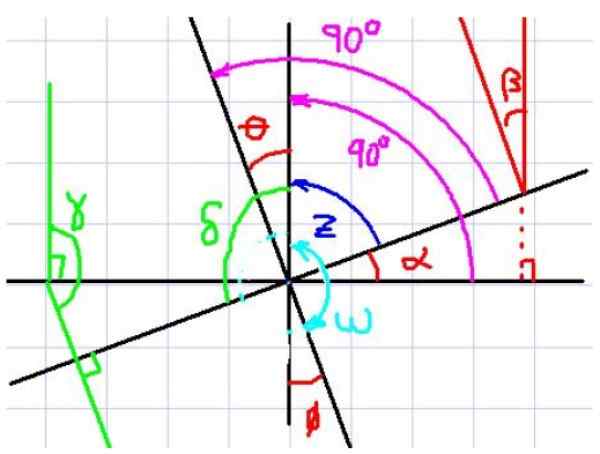Rysunek 4. Kąty prostopadłe. Źródło: f. Zapata.

Na przykład na rycinie 4 kąt α i θ. Teraz zauważ, że każdy kąt ma odpowiedni prostopadle pod drugim kątem.

Widać również, że α i θ mają ten sam kąt uzupełniający z, Dlatego obserwator natychmiast stwierdza, że ​​α i θ mają tę samą miarę. Wydaje się wtedy, że jeśli dwa kąty mają ze sobą prostopadłe strony, są takie same, ale zobaczmy inny przypadek.

Teraz rozważ kąty α i ω. Te dwa kąty mają również odpowiednie prostopadłe strony, jednak nie można powiedzieć, że są one równe, ponieważ jedno jest ostre, a drugi tępy.

Zauważ, że ω + θ = 180º. Oprócz θ = α. Jeśli zastąpisz to wyrażenie Z w pierwszym otrzymywanym równaniu:

δ + α = 180º, ponieważ δ i α są kątami wzajemnie prostopadłych.

Ogólna zasada dla stron prostopadłych 

Na podstawie wyżej wymienionych można ustalić zasadę, która jest zawsze spełniona, że ​​kąty mają prostopadłe strony:

Jeśli dwa kąty są wzajemnie prostopadłe, są takie same, jeśli oba są ostre lub oba są tępe. W przeciwnym razie, jeśli jedno jest ostre, a drugi tępy, to są dodatkowe, to znaczy dodają 180º.

Stosując tę ​​zasadę i w odniesieniu do kąty z rysunku 4 możemy potwierdzić następujące czynności:

α = β = θ = φ

γ = δ

Z dodatkowym kątem α, β, θ i φ.

Bibliografia

1. Baldor, J. DO. 1973. Płaska i przestrzeń geometria. Cultural American Cultural. 
2. Prawa i formuły matematyczne. Systemy pomiaru kąta. Pobrano z: Ingemecanica.com.
3. Wentworth, G. Geometria planety. Odzyskane z: Gutenberg.org.
4. Wikipedia. Kąty komplementarne. Odzyskane z: jest.Wikipedia.com
5. Wikipedia. Przenośnik. Odzyskane z: jest.Wikipedia.com
6. Zapata f. Goniometr: historia, części, operacja. Pobrano z: Lifer.com