Właściwości symetrii osiowej, przykłady i ćwiczenia

Symetria osiowa Występuje, gdy punkty figury pokrywają się z punktami innej figury za pomocą prostej meditrix zwanej osi symetrii. Nazywa się to również symetrią promieniową, obrotową lub cylindryczną.

Zazwyczaj jest stosowany w postaci geometrycznej, ale można go łatwo obserwować w naturze, ponieważ istnieją zwierzęta, takie jak motyle, skorpiony, półki lub prawidłowo ludzie, które przedstawiają symetrię osiową.

Na tym zdjęciu horyzontu miasta Toronto i jego odbicie w symetrii osiowej wody. (Źródło: Pixabay)

[TOC]

Jak znaleźć symetryczny osiowy

Aby znaleźć symetryczny osiowy p 'punktu p w odniesieniu do linii (L) Wykonane są następujące operacje geometryczne:

1.- Święto prostopadłe do linii (L), które przechodzi przez punkt P.

2.- Przechwycenie dwóch linii określa punkt lub.

3.- Długość segmentu PO jest mierzona, wówczas długość ta jest kopiowana na linii (PO), zaczynając od lub w kierunku p a lub określając punkt p '.

4.- Punkt p.

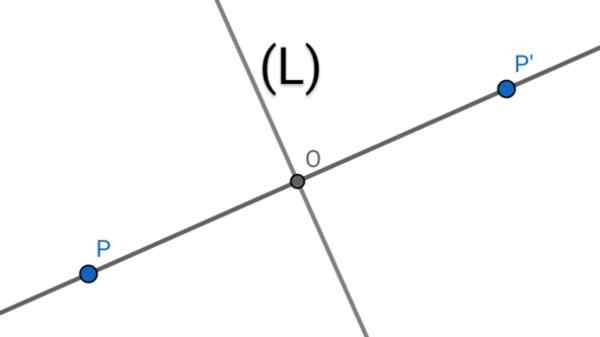Rysunek 1. Dwa punkty P i P 'są osiowo symetryczne do osi (L), jeśli wspomniana oś jest meditrix segmentu PP'

Właściwości symetrii osiowej

- Symetria osiowa jest izometryczna, to znaczy odległości figury geometrycznej i odpowiadające jej symetryczne.

- Miara kąta i jego symetrycznych jest taka sama.

- Symetryczny osiowy punkt punktu na osi symetrii jest samym punktem.

Może ci służyć: Gauss-Seidel Metoda: Objaśnienie, aplikacje, przykłady

- Symetryczna linia linii równoległej do osi symetrii jest również stoiskiem równoległym do wspomnianej osi.

- Linia sekundowa do osi symetrii jest symetryczna.

- Symetryczny obraz linii to inna linia, która tworzy kąt z osi symetrii o tej samej miarie, co oryginalna linia.

- Symetryczny obraz linii prostopadłej do osi symetrii to kolejna linia, która zachodzi za pierwszą.

- Linia i jej osiowa linia symetryczna tworzą kąt, którego dwusa'a jest oś symetrii.

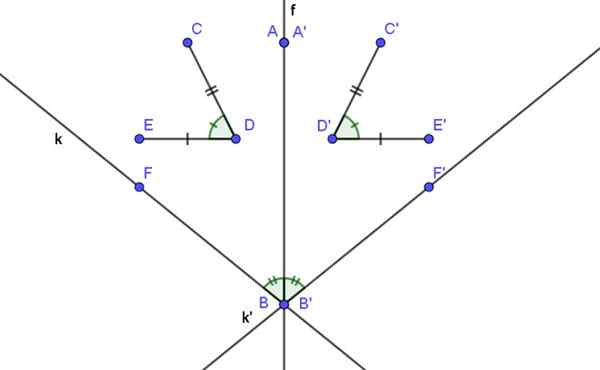Rysunek 2. Symetria osiowa zachowuje odległości i kąty.

Przykłady osiowej symetrii

Natura wykazuje obfite przykłady symetrii osiowej. Na przykład możesz zobaczyć symetrię twarzy owadów, takich jak motyle, odbicie na powierzchniach spokojnych wód i luster lub liści roślin, między innymi.

Rysunek 3. Ten motyl wykazuje prawie idealną symetrię osiową. (Źródło: Pixabay) Rysunek 4. Twarz tej dziewczyny ma osiową symetrię. (Źródło: Pixabay)

Ćwiczenia symetrii osiowej

Ćwiczenie 1

Masz trójkąt wierzchołków A, B i C, których współrzędne kartezjańskie są odpowiednio A = (2, 5), B = (1, 1) i C = (3,3). Znajdź współrzędne kartezjańskie trójkąta symetrycznego w odniesieniu do osi y (oś zarządzenia).

Rozwiązanie: Jeśli punkt P ma współrzędne (x, y), wówczas jego symetryczny w odniesieniu do osi rzędnych (oś) wynosi p '= (-x, y). Innymi słowy.

Może ci służyć: nieskończony zestaw: właściwości, przykłady

W tym przypadku symetryczny trójkąt wierzchołków a ', b' i c 'będzie miał współrzędne:

A '= (-2, 5); B '= (-1, 1) i C' = (-3, 3), co można sprawdzić na rysunku 6.

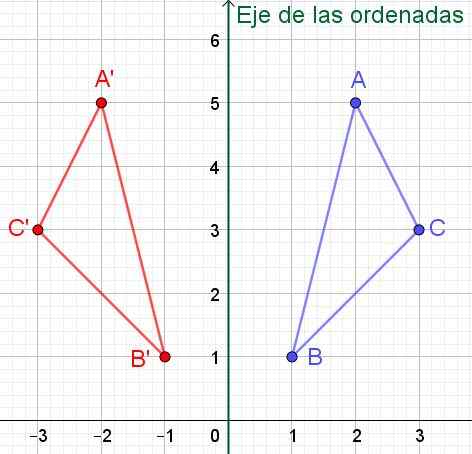Rysunek 6. Jeśli punkt ma współrzędne (x, y) jego symetryczne w odniesieniu do osi y (oś zarządzenia) będzie miało współrzędne (-x, y).

Ćwiczenie 2

W odniesieniu do trójkąta ABC i jego symetrycznego a'b'c 'Ćwiczenia 1 sprawdź, czy odpowiednie strony oryginalnego trójkąta i jego symetryczne mają taką samą długość.

Rozwiązanie: Aby znaleźć odległość lub długość boków, używamy wzoru odległości euklidianowej:

d (a, b) = √ ((bx-ax)^2 + (przez-ay)^2) = √ ((1-2)^2 + (1-5)^2) = √ ((-1 )^2 + (-4)^2) = √ (17) = 4,123

Następnie oblicza się długość symetrycznej strony odpowiadającej'B ':

D (a ', b') = √ ((bx'-ax ')^2 +(by'-y^2) = √ ((-1 +2)^2 +(1-5)^2) = √ ((1)^2 + (-4)^2) = √ (17) = 4 123

W ten sposób udowodniono, że osiowa symetria zachowuje odległość między dwoma punktami. Procedurę można powtórzyć dla pozostałych dwóch stron trójkąta, a jej symetryczne, aby sprawdzić niezmienność na długości. Na przykład | AC | = | A'c '| = √5 = 2236.

Ćwiczenie 3

W odniesieniu do trójkąta ABC i jego symetrycznego a'b'c 'Ćwiczenia 1 sprawdź, czy odpowiednie kąty oryginalnego trójkąta i ich symetryczne mają tę samą miarę kątową.

Rozwiązanie: Aby określić pomiary kątów BAC i B'a'c 'Produkt skalarny wektorów zostanie najpierw obliczony Ab z AC a potem produkt skalarny A'b ' z A'c '.

Pamiętając o tym:

A = (2, 5), B = (1, 1) i C = (3,3)

A '= (-2, 5); B '= (-1, 1) i C' = (-3, 3).

Ty masz:

Ab = y AC =

podobnie

A'b ' = y AC =

Może ci służyć: twierdzenie Lamy

Następnie znaleziono następujące produkty skalarne:

Ab⋅ac = ⋅ = -1⋅1 + (-4) ⋅ (-2) = -1 + 8 = 7

podobnie

A'B'lEa'c ' = ⋅ = 1⋅ (-1) + (-4) ⋅ (-2) = -1 + 8 = 7

Miara kąta BAC to:

∡Bac = arccos ( Ab⋅ac / (|AB |⋅ |AC |)) = 

Arccos (7 / (4,123⋅2,236)) = 40,6º

Podobnie miara kąta B'a'c 'to:

∡b'a'c '= arccos ( A'B'lEa'c ' / (|A'B '|⋅ |A'c '|)) = 

Arccos (7 / (4,123⋅2,236)) = 40,6º

Stwierdzenie, że osiowa symetria zachowuje miarę kąta.

Ćwiczenie 4

Być punktem P współrzędnej (a, b). Znajdź współrzędne jego symetrycznego osiowego p 'w odniesieniu do linii y = x.

Rozwiązanie: Nazwimy (a ', b') do współrzędnych punktu symetrycznego p 'w odniesieniu do linii y = x. Punkt środkowy M segmentu PP „ma współrzędne ((a+a ')/2, (b+b')/2) i znajduje się również na linii y = x, więc spełniono następującą równość:

A + A '= B + B'

Z drugiej strony segment PP „oczekuje -1 za to, że jest prostopadle do linii y = x nachylenia 1, więc spełniono następującą równość:

B - b '= a' -a

Wyczyszczenie dwóch równości przed „i b” stwierdzono, że:

a '= b i co b' = a.

To znaczy, biorąc pod uwagę punkt P (a, b), jego symetryczny osiowy w odniesieniu do linii y = x to p '(b, a).

Bibliografia

1. Arce m., Blázquez S i inni. Transformacje samolotowe. Odzyskane z: educutmxli.Akta.WordPress.com
2. Obliczenie CC. Symetria osiowa. Odzyskane z: Obliczanie.DC
3. Superprof. Symetria osiowa. Odzyskane z: Superprof.Jest
4. Wikipedia. Symetria osiowa. Odzyskane z: jest.Wikipedia.com
5. Wikipedia. Symmetryczna okólnik. Źródło: w:.Wikipedia.com