Wyjaśnienie warunków drugiej równowagi, przykłady, ćwiczenia

Drugi warunek równowagi Stwierdza, że ​​suma momentów lub momentów wytwarzanych przez wszystkie siły, które działają na ciele, niezależnie od obliczania, musi zostać unieważnione, aby wspomniane ciało jest w równowadze statycznej lub dynamicznej równowagi.

Oznaczanie momentu obrotowego lub momentu siły przez grecki litera τ, matematycznie wyraża się to w następujący sposób:

∑ τ = 0

Rysunek 1. Aby zrównoważyć rocker, konieczne jest zastosowanie drugiego stanu równowagi. Źródło: Pxhere.

Odważna litera wskazuje wektorowy charakter momentu, który należy unieważnić w odniesieniu do dowolnego punktu wybranego jako centrum wirowania. W ten sposób, anulowanie momentu obrotowego netto, gwarantowane jest, że obiekt nie zacznie się obracać ani obracać.

Jeśli jednak obiekt już się obracał, a moment obrotowy netto znika nagle, obrót będzie kontynuowany, ale przy stałej szybkości kątowej.

Drugi warunek równowagi jest stosowany w połączeniu z pierwszą warunkami, która mówi, że suma sił na ciele musi być nieważna, tak aby się nie poruszała lub że jeśli tak, jest z jednolitym ruchem prostoliniowym:

∑ F = 0

Oba warunki mają zastosowanie do rozszerzonych ciał, tych, których wymiary są mierzalne. Kiedy obiekt ma być cząsteczką, nie ma sensu mówić o rotacjach, a pierwszy warunek zagwarantowania równowagi jest wystarczający.

Przykłady

Drugi warunek równowagi ujawnia się w niezliczonych sytuacjach:

Podczas wspinania się po schodach

Wspierając schody na podłodze i ścianie, potrzebujemy wystarczającej ilości wcierania, szczególnie na podłodze, aby schody się nie poślizgnęły. Jeśli spróbujemy wspinać się na drabinę wspieraną na tłustej, mokrej lub śliskiej podłodze, nie jest trudno przewidzieć, że upadniemy.

Aby móc pewnie używać schodów, konieczne jest, aby była w równowadze statycznej podczas wspinaczki, a kiedy jest w potrzebnym kroku.

Może ci służyć: Pluton (Planet Dwarf))

Poruszanie szafy

Kiedy chcesz przenieść wysokie meble jako szafę lub dowolny kawałek, którego wysoki jest większy niż szeroki, wygodne jest pchanie w niskim punkcie, aby uniknąć obalenia, w ten sposób bardziej prawdopodobne jest, że meble zsuną się odwracania się i położenia.

W takich okolicznościach meble niekoniecznie są w równowadze, ponieważ można je szybko przesuwać, ale przynajmniej nie odwróci się.

Balkony

Balkony, które wyróżniają budynki, muszą być zbudowane, gwarantując, że chociaż na górze jest wiele osób, nie obraca się i nie zapadają.

Dielektryk w zewnętrznych polach elektrycznych

Podczas umieszczania materiału dielektrycznego w zewnętrznym polu elektrycznym cząsteczki poruszają się i obracają, aby przyjąć pozycję równowagi, tworząc pole elektryczne wewnątrz materiału.

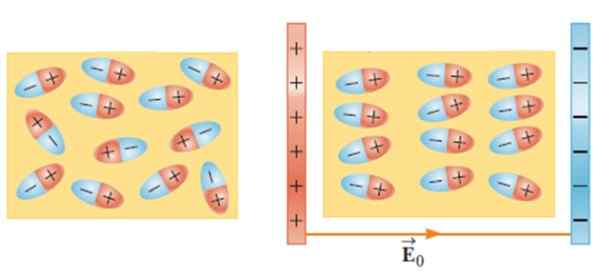Rysunek 2.- Bez zewnętrznego pola elektrycznego dipole są losowe (po lewej). Pole zewnętrzne stosuje moment obrotowy na cząsteczkach dielektrycznych i są one reorganizowane. Źródło: Serway, r. Fizyka nauk i inżynierii.

Efekt ten powoduje, że pojemność kondensatora wzrasta, gdy między jego pancerzem wprowadza się materiał, taki jak szkło, guma, papier lub olej.

Znaki i lampy

Wiele pomieszczeń często zawiesza zawiadomienia na ścianie budynku, aby były widoczne dla przechodniów.

Plakat jest przymocowany przez pręt i kabel, oba przymocowane na ścianie za pomocą podporowych. Różne siły, które działają, muszą zapewnić, że plakat nie spadnie, dla których dwa warunki równowagi wchodzą w działanie.

W ten sposób można również umieścić reflektor w parku, jak na poniższym rysunku:

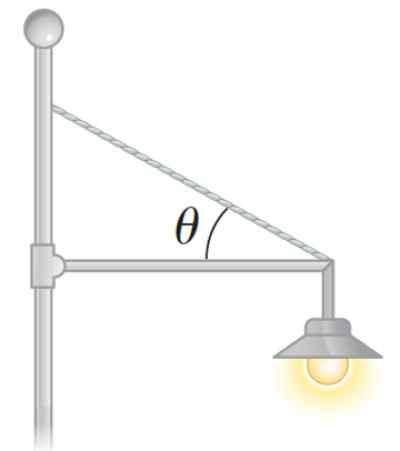Rysunek 3. Statyczna lampa bilansowa. Źródło: Serway. Fizyka nauk i inżynierii.

Jak obliczyć moment netto lub moment siły netto?

Moment obrotowy lub moment siły, oznaczony przez τ albo M W niektórych tekstach jest zawsze obliczany w odniesieniu do pewnego punktu, w którym przechodzi oś obrotu.

Jest zdefiniowany jako produkt wektorowy między wektorem pozycji R, to jest skierowane ze wspomnianej osi do punktu stosowania siły i siły F:

Może ci służyć: Bilans termodynamiczny: Zajęcia i zastosowania

τ = R × F

Będąc wektorem, należy wyrazić moment obrotowy, nadając jego wielkość, kierunek i znaczenie. Wielkość jest podana przez:

τ = rf.sin θ

Właściwa zasada dla produktu wektorowego

Gdy problem znajduje się w płaszczyźnie, adres momentu obrotowego jest prostopadły do ​​papieru lub ekranu, a kierunek jest określany przez zasadę prawej ręki, w której wskaźnik wskazuje R, Środkowy palec w kierunku F a kciuki sygnalizują lub poza papierem.

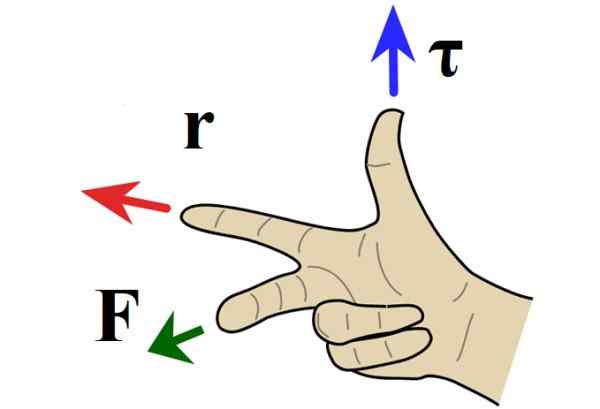Rysunek 4. Reguła prawej ręki dla produktu wektorowego. Źródło: Wikimedia Commons.

Gdy moment obrotowy wskazuje z papieru, obrót znajduje się w przeciwnym kierunku do igieł zegara i jest przypisany znakowi pozytywnemu. Jeśli zamiast tego moment obrotowy jest skierowany w arkuszu, obrót znajduje się w kierunku dłoni i znaku ujemnego.

Aby znaleźć moment obrotowy netto, wybrany jest wygodny punkt obliczeń, który może być ten, w którym działa największa ilość sił. W tym przypadku moment tych sił jest nieważny, ponieważ posiadanie wektora pozycji R wielkości 0.

Możesz wybrać dowolny punkt, który oferuje wystarczającą ilość informacji, aby wyczyścić nieznane, które prosi o rozwiązanie problemu. Zobaczmy to bardziej szczegółowo.

Ćwiczenie rozwiązane

Reflektor poniższej liczby ma 20 kg masy i jest wspierany przez poziomy cienki pręt, o nikczemnej masie i długości L, który jest wyartykułowany na stanowisku. Kabel, również światło, który pomaga utrzymać odbłyśnik, tworzy kąt θ = 30 °. Oblicz:

a) Napięcie w kablu

b) wielkość siły F, którą słupek wywiera na pasek przez zawias.

Rozwiązanie

Zastosujemy pierwszy warunek równowagi ∑ F = 0 do sił pokazanych na schemacie:

Może ci służyć: pochłaniane ciepło: wzory, jak je obliczyć i rozwiązane ćwiczenia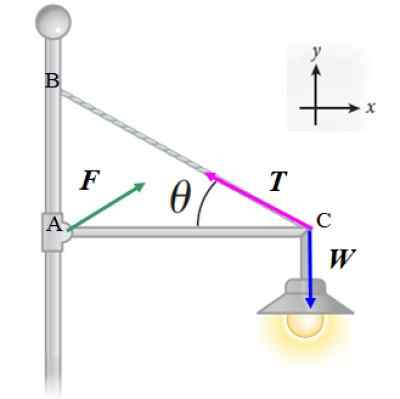

F + T + W = 0

Zauważ, że wielkość i kierunek F Nie zostały jeszcze ustalone, ale zakładamy, że ma dwa elementy: F_X i f_I. W ten sposób otrzymujemy dwa równania:

F_X -T. cos θ = 0

F_I - W + T⋅ sin θ = 0

Teraz zastosujmy drugą warunek równowagi, wybierając punkt A, ponieważ nie znamy wielkości F ani to T. Wybierając ten punkt, wektor R_DO jest nieważne, a zatem moment F jest nieważne i wielkość F Nie pojawi się w równaniu:

-W⋅L + T⋅Sen θ⋅l = 0

Dlatego:

T.sin θ.L = w.L

T = w/sen θ = (20 kg x 9.8 m/s²) / Sin 30 º = 392 n

Znając wielkość t, możemy wyczyścić komponent F_X:

F_X = T⋅ cos θ = 392 cos 30º n = 339. 5 n

A następnie komponent f_I:

F_I = W - T⋅ sin θ = (20 kg x 9.8 m/s²) - 392⋅Sen 30 º = 0

Wtedy możemy wyrazić F Więc:

F = 339.5 n X

Jest to zatem siła pozioma. To dlatego, że uważamy, że bar miał godną pogoni na wadze.

Jeśli wybrano punkt C do obliczenia wynikowego momentu, wektory R_T I R_W Dlatego są null:

M = f_Y⋅L = 0

Stwierdzono, że F_I = 0. Zatem:

- W + T⋅ sin θ = 0

T = w/ sin θ

Który jest ten sam wynik początkowo uzyskany, wybierając punkt A jako miejsce, w którym przechodzi oś obrotu.

Interesujące tematy

Warunki równowagi.

First Bilans Warunek.

Bibliografia

1. Bedford, 2000. DO. Mechanika inżynierii: statyczne. Addison Wesley.
2. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 4. Układy cząstek. Pod redakcją Douglas Figueroa (USB).
3. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6th. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1.
5. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. 7th. Wyd. Cengage Learning.