Kąty w typach obwodu, właściwości, ćwiczenia rozstrzygnięte

Zwany Kąty o obwodzie do tych, w których którykolwiek z jego elementów jest lub przecina się z danym obwodem. Wśród nich są następujące:

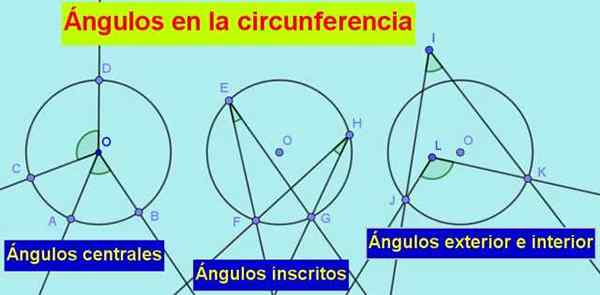
1.- On Kąt centralny, którego wierzchołek znajduje się w środku obwodu, a jego boki suszy się do niego, jak widzimy na następującym obrazie:

Rysunek 1. Rodzaje kątów w obwodzie to: środkowe, wpisane, zewnętrzne i wnętrza. Źródło: f. Zapata.

2.- On Zarejestrowany kąt, którego wierzchołek jest na obwodzie, a jego boki są suche lub styczne do obwodu.

3.- Kąt zewnętrzny, którego wierzchołek jest poza obwodem, ale jego boki są suche lub styczne do obwodu.

4.- On Kąt wewnętrzny, z wierzchołkiem wewnątrz obwodu i jego suchymi stronami do tego samego.

Wszystkie te kąty zachowują pewne relacje ze sobą, co prowadzi nas do ważnych właściwości między kątami należącymi do danego obwodu.

[TOC]

Nieruchomości

- Kąt centralny

Kąt centralny jest definiowany jako ten, którego wierzchołek znajduje się w środku obwodu, a jego boki wycięte w obwodzie.

Miara promieniowego kąta centralnego jest ilorazem między łukiem, który subtacjonuje, to znaczy łukiem obwodu między bokami kąta i promieniem obwodu. 

Jeśli obwód jest jednolity, to znaczy promień 1, wówczas miara kąta środkowego jest długością łuku, co odpowiada liczbie radian.

Jeśli chcesz miary kąta centralnego w stopniach, miara jest mnożona w radianach przez współczynnik 180º/π.

Instrumenty pomiarowe kątów, takie jak transporter i goniometr, zawsze używają kąta centralnego i długości substancji rozpadłego łuku.

Może ci służyć: częściowe pochodne: właściwości, obliczenia, ćwiczenia

Są one skalibrowane w stopniach seksualnych, co oznacza, że ​​za każdym razem, gdy mierzony jest kąt, z tyłu, co jest mierzone.

Nieruchomość

Miara kąta centralnego w radianach jest równa długości łuku, która subtin lub przechwyty podzielone przez długość promienia.

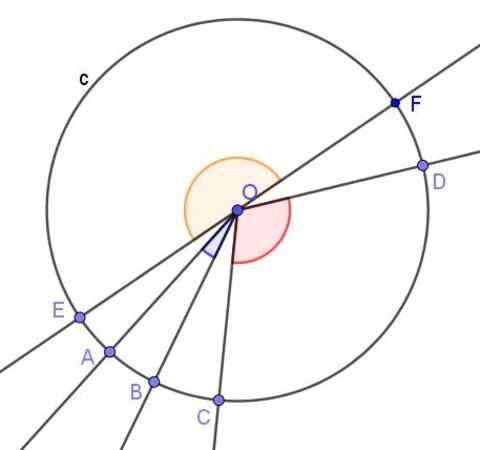Rysunek 2. Pokazano trzy kąty centralne. Jeden ostry, drugi tępy i jeden płaski. Źródło: f. Zapata.

- Zarejestrowany kąt

Zarejestrowany kąt obwodu to taki, który ma swój wierzchołek na obwodzie, a jego półstaight są suche lub styczne do tego samego. 

Jego właściwości to:

Nieruchomości

-Zarejestrowany kąt jest wypukły lub płaski.

-Gdy zapisany kąt przechwytuje ten sam łuk co kąt środkowy, miara pierwszego będzie połowa drugiego.

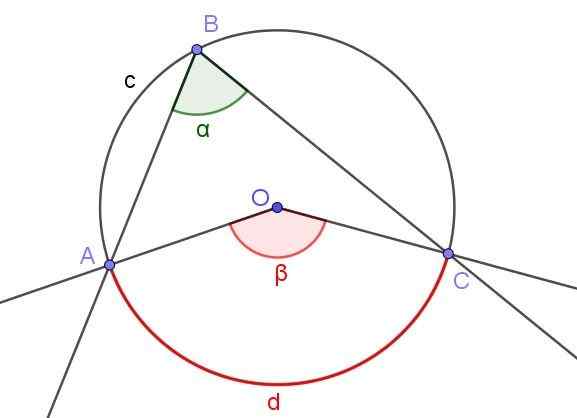Rysunek 3. Zarejestrowany kąt ∠ABC i kąt centralny ∠AOC, który podzielony na ten sam łuk A⌒c. Źródło: f. Zapata.

Rysunek 3 pokazuje dwa kąty ∠ABC i ∠AOC, które przechwytują ten sam łuk obwodu A⌒c.

Jeżeli miara zarejestrowanego kąta jest α, wówczas miara β kąta centralnego jest dwukrotnie większą niż miara zarejestrowanego kąta (β = 2 α), ponieważ oba odejmują ten sam zmierzony łuk D.

- Kąt zewnętrzny

Jest to kąt, którego wierzchołek jest poza obwodem, a każda z jego boków przecina obwód w jednym lub większej liczbie punktów.

Nieruchomość

-Jego miara jest równa pół -ekspresji (lub różnicy podzielonej przez 2) kątów centralnych, które przechwytują same łuki.

Aby upewnić się, że miara jest dodatnia, półprepresy powinno być zawsze centralnym kątem największej miary mniejszej miary dolnego kąta środkowego, jak pokazano na poniższym rysunku.

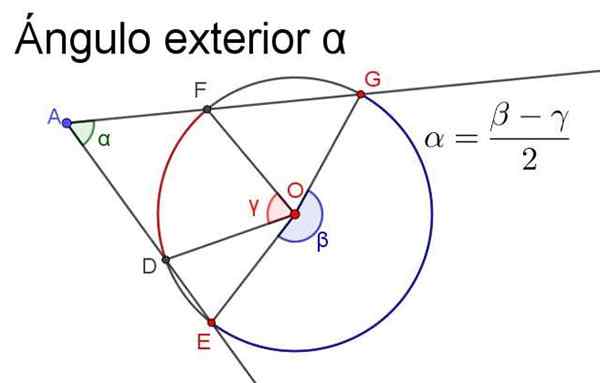Rysunek 4. Kąt zewnętrzny α jest równy półprzezroczce centrów, które podtrzymują te same łuki. Źródło: f. Zapata.

- Kąt wewnętrzny

Kąt wewnętrzny jest tym, którego wierzchołek znajduje się wewnątrz obwodu, a jego boki przecinane do obwodu.

Może ci służyć: współczynnik determinacji: wzory, obliczenia, interpretacja, przykłady

Nieruchomość 

Jego miara jest równa pół -grupie kąta środkowego, który subteluje ten sam łuk, plus kąt centralny, który subteluje ten sam łuk, co kąt wydłużenia (jest to kąt wewnętrzny utworzony przez pół -straight uzupełniający się do kątów oryginału Kąt wewnętrzny).

Poniższy rysunek ilustruje i wyjaśnia własność wewnętrznego kąta.

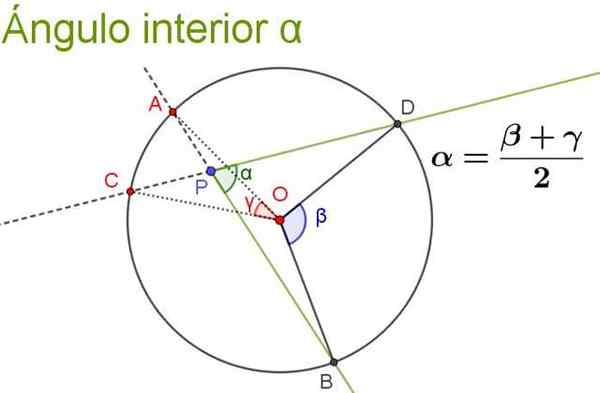Rysunek 5. Wewnętrzny kąt α jest równy półsysezmowi kątów centralnych, które podtrzymują te same łuki, co on sam. Źródło: f. Zapata.

Rozwiązane ćwiczenia

- Ćwiczenie 1

Załóżmy, że wpisany kąt, w którym jedna z jego stron przechodzi przez środek obwodu, jak pokazano na rycinie 6. Promień obwodu wynosi oa = 3 cm, a łuk ma długość π/2 cm. Określić wartość kąty α i β.

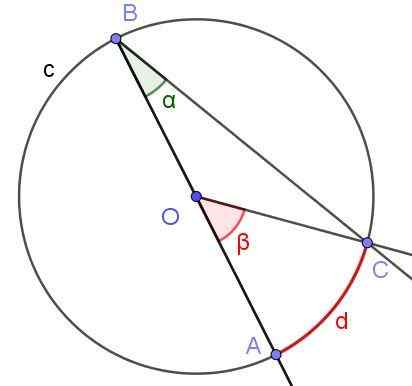Rysunek 6. Zarejestrowany kąt ∠ABC z bokiem [BA) przez O i kąt centralny ∠AOC.Źródło: f. Zapata.

Rozwiązanie

W tym przypadku powstaje trójkąt Isosceles COB, ponieważ [OC] = [OB]. W trójkącie Isosceles kąty przylegające do podstawy są takie same, dlatego muszą one ci. Z drugiej strony ∠COB = 180º - β. Biorąc pod uwagę sumę wewnętrznych kątów trójkąta COB:

α + α + (180º - β) = 180º

Z miejsca, w którym wynika, że ​​2 α = β lub co jest równoważne α = β/2, co potwierdza właściwość (3) poprzedniej sekcji, że miara zarejestrowanego kąta jest połowa kąta środkowego, gdy oba kąty odejmują Ta sama lina [AC].

Teraz ustalamy wartości numeryczne: kąt β jest centralny, a jego miarą w radiach jest stosunek między łukiem a promieniem r = OA, więc jego miara wynosi:

β = d / r = (π / 2 cm) / (3 cm) = π / 6 rad = 30º.

Może ci służyć: czworobok: elementy, właściwości, klasyfikacja, przykłady

Z drugiej strony już potwierdzono, że α = β / 2 = (π / 6 rad) / 2 = π / 12 rad = 15º. 

- Ćwiczenie 2

Na rycinie 7 kąty α₁ i β₂ mieć tę samą miarę. Ponadto kąt β₁ Mierzy 60º. Określ kąty β i α.

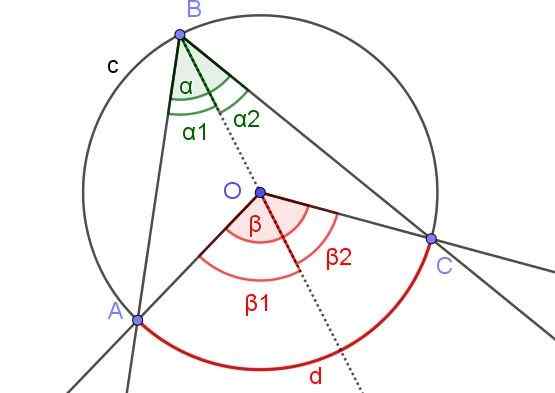Rysunek 7. Na rysunku α₁ = β₂ i β₁ = 60º. Określ wartości β i α. Źródło: f. Zapata.

Rozwiązanie

W takim przypadku istnieje wpisany kąt ∠ABC, w którym środek lub obwód znajduje się wewnątrz kąt.

Z powodu właściwości (3) masz α₂ = β₂ /2 i α₁ = β₁ /2. Jak:

α = α₁ + α₂ i β = β₁ + β₂

Dlatego masz:

α = α₁ + α₂ = β₁ /2 + β₂ /2 = (β₁ + β₂) / 2 = β / 2.

To znaczy, zgodnie z właściwościami:

α = β / 2

Jak powiedziano nam, że β₁ = 60º W takim razie:

α₁ = β₁ / 2 = 60º / 2 = 30º.

Mówią nam również, że α₁ = β₂ Wynika więc:

β₂ = 30º.

Kąt β to:

β₁ + β₂ = 60º + 30º = 90º.

I jako α = β / 2, zatem:

α = 90º / 2 = 45º. 

Podsumowując:

β = 90º i α = 45º.

Bibliografia

1. Baldor, a. 1973. Geometria i trygonometria. Redakcja kulturalna Ameryki Środkowej.
2. I. DO. 2003. Elementy geometrii: z ćwiczeniami i geometrią kompasu. University of Medellin.
3. Geometria 1st. Kąty w obwodzie. Odzyskane z: edu.Xunta.Jest.
4. Cała nauka. Rozwiązane ćwiczenia kątów w obwodzie. Odzyskane z: Francessphysics.Blogspot.com
5. Wikipedia. Zarejestrowany kąt. Odzyskane z: jest.Wikipedia.com