Segment prosty i półprzezroczysty

Linia linii i półright są zróżnicowane pod względem faktu, że segment linii jest ograniczony; to znaczy ich początkowy punkt i punkt końcowy są znane. Z pół -prawu jest znany jego początkowy punkt, ale nie punkt końcowy, ponieważ rozciąga się na nieskończoność.

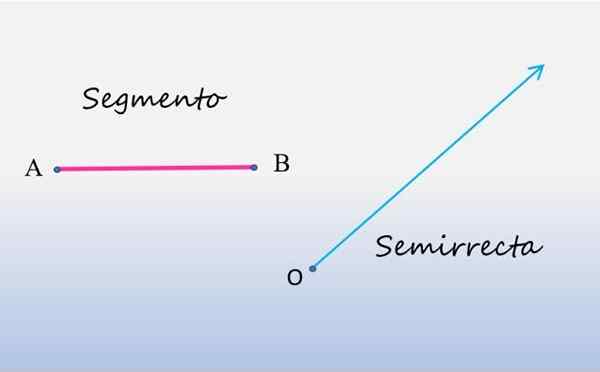
Poniższy rysunek pokazuje, po lewej stronie, segment linii i po prawej, pół -prawy:

Segment i półright. Źródło: f. Zapata.

Jak widać, segment jest linią linii, która zaczyna się w punkcie A i kończy w punkcie B, a punkty te to końce wspomnianego segmentu. Pomiar segmentu odpowiada długości między jego końcami.

Ze swojej strony pół -prawe ma swój punkt wyjścia w punkcie O i rozciąga się na nieskończoność, co jest równoważne, że jest ograniczony tylko jednym końcem, zwykle nazywanym pochodzeniem. Z tego powodu są również nazywane Wielkie nieba.

Segmenty są oznaczone przez litery wskazujące punkt początkowy i koniec. Na przykład segment figury to segment AB lub skok jest umieszczony na wierzchu, tak:

Z drugiej strony można również wyznaczyć półprzezroczyste z dwoma literami, jeden wskazuje punkt odpowiadający pochodzeniem, a drugi dodatkowy list. Można go również użyć niewielkiej litery do reprezentowania błyskawicy lub półreakcji, a także są półstaight z własną imieniem, co będzie widać w przykładach później.

Przykłady segmentów

Segmenty są bardzo ważne w geometrii, poniżej są jedne z najbardziej godnych uwagi:

Boki wielokąta

Wielokąty są płaskie i zamknięte postacie, których boki to nie -konsekwentne segmenty linii. Na przykład trójkąt ma trzy strony, czworokąt ma cztery strony, Pentagon ma pięć i tak dalej.

Może ci służyć: Tesseldos: Charakterystyka, typy (regularne, nieregularne), przykłady

Średnica obwodu

Jest zdefiniowany jako ten segment, który zawiera dwa punkty obwodu i koniecznie przechodzi przez środek tego samego.

Lina obwodu

Kiedy segment, który dołącza do dwóch punktów obwodu, nie przechodzi przez jego centrum, nazywa się to liną.

Wysokość trójkąta

Wysokość trójkąta jest zdefiniowana jako segment, który przechodzi prostopadle z jednej z boków trójkąta do przeciwnego wierzchołka. Jeżeli miara podstawy trójkąta zwanego B i wysokość tego samego, oznaczona jako H jest znana, obszar A tego samego jest obliczany przez dobrze znaną formułę:

A = ½ b ∙ h

Semirretowe przykłady

Semi -Steright są również bardzo ważnymi elementami geometrii. Niektóre dobrze znane półprzestrzeni to:

Pozytywne półki

Trzy kierunki w przestrzeni: wysokie, szerokie i głębokie, mogą być reprezentowane przez układ osi kartezjańskich, składający się z trzech wzajemnie prostopadłych linii, oznaczonych jako osi X, I I z, które są wycięte w punkcie nazywanym pochodzenie.

Ten przepis dzieli przestrzeń na osiem regionów znanych jako Octaczniki. Na poniższym rysunku obserwuje się pozytywne półki X, I I z, które określają pierwszą okant. Podobnie, pozytywne pół -x y określają obszar zwanego płaszczyzny Pierwszy kwadrant.

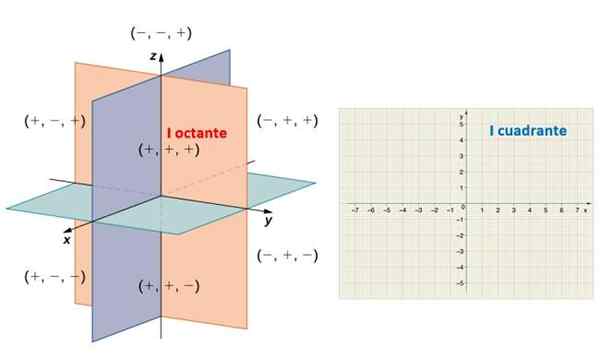Po lewej, osiem oktantów przestrzeni i po prawej, płaszczyzna kartezjańska podzielona na cztery ćwiartki. Źródło: Math Librettexts.

Boki kąta

Kąt to ułamek płaszczyzny, która jest wyznaczona przez dwa półprzestrzenne, których pochodzenie jest wspólne. Ten punkt wspólnego jest wierzchołek kąta, podczas gdy półprzestrzenny są odpowiednio, początkowa strona i końcowa strona kąta. Taki przepis pokazano na poniższym rysunku:

Może ci służyć: jaki jest związek między obszarem Rhombusa a prostokątem?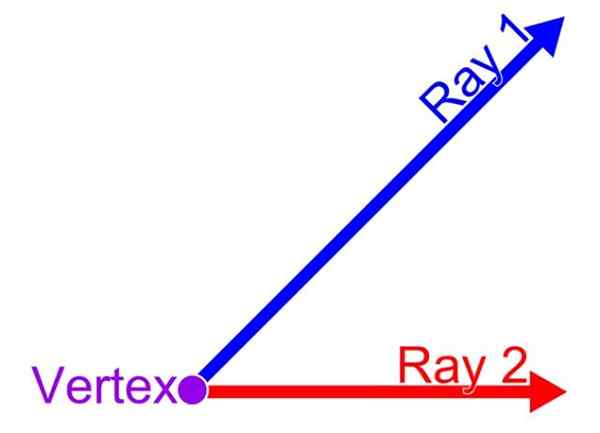 Elementy kąta. Źródło: Wikimedia Commons.