Schowers

Wyjaśniamy, jaka jest zasada Sturges, jej zastosowanie i podajemy kilka przykładów

Jaka jest zasada Sturges?

Schowers Jest to kryterium użyte do określenia liczby klas lub interwałów, które są niezbędne do wykresu zestawu danych statystycznych graficznych. Zasada ta została podana w 1926 roku przez niemieckiego matematyka Herberta Sturgesa.

Sturges zaproponował prostą metodę, oparta na liczbie x próbek, które pozwoliły znaleźć liczbę klas i ich zakres. Reguła Sturges jest szeroko stosowana przede wszystkim w obszarze statystyki, szczególnie do budowy histogramów częstotliwości.

Wyjaśnienie

Reguła Sturges jest metodą empiryczną szeroko stosowaną w statystykach opisowych w celu ustalenia liczby klas, które muszą istnieć w histogramie częstotliwości, aby sklasyfikować zestaw danych reprezentujących próbkę lub populację.

Zasadniczo ta reguła określa szerokość pojemników graficznych, histogramy częstotliwości.

Aby ustalić swoją zasadę Herbert Sturges uznany za idealny schemat częstotliwości, który składa się z K interwałów, w których interwał I zawiera pewną liczbę próbek (i = 0,… k - 1), reprezentowany jako:

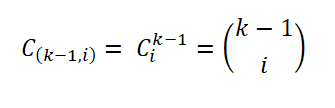
Ta liczba próbek jest podana przez liczbę sposobów wyodrębnienia podzbioru zestawu; to znaczy przez współczynnik dwumianowy wyrażony w następujący sposób:

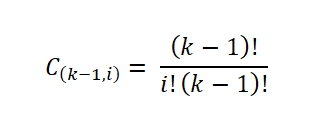Następnie Sturges powiązał, że histogram częstotliwości przybliża rozkład normalny, gdy liczba przedziałów (k) wzrośnie zgodnie z centralnym twierdzeniem o granicy. W taki sposób, że można obliczyć liczbę próbek każdego z przedziałów:

Może ci służyć: ENEGON: Właściwości, jak zrobić engon, przykłady

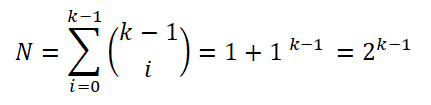
Aby uprościć wyrażenie, zastosował właściwości logarytmów w obu częściach równania:

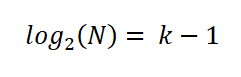
W ten sposób Sturges ustalił, że optymalna liczba K przedziałów jest podana przez wyrażenie:

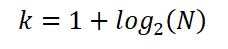
Można go również wyrazić jako:

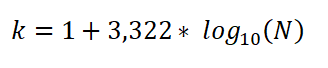
W tym wyrażeniu:

• K to liczba klas.
• N to całkowita liczba obserwacji w próbce.
• Log jest wspólnym logarytmem podstawowym 10.

Na przykład, aby opracować histogram częstotliwości, który wyraża losową próbkę wzrostu 142 dzieci, liczba przedziałów lub klas, które będzie miał rozkład, wynosi:

K = 1 + 3322 _* dziennik₁₀ (N)

K = 1+3322_* Log (142)

K = 1+3322_* 21523

K = 8,14 ≈ 8

Zatem rozkład będzie w 8 przedziałach.

Liczba interwałów musi być zawsze reprezentowana przez liczby. W przypadkach, gdy wartość jest dziesiętna, należy dokonać przybliżenia najbliższej liczby całkowitej.

Sturges zastosowania reguł

Reguła Sturges jest stosowana głównie w statystykach, ponieważ umożliwia rozkład częstotliwości poprzez obliczenie liczby klas (k), a także długości każdej z nich, znanej również jako amplituda.

Amplituda jest różnicą w górnej i dolnej granicy klasy, podzielonej przez liczbę klas i jest wyrażona:

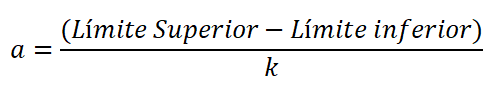
Istnieje wiele reguł empirycznych, które umożliwiają rozkład częstotliwości. Jednak reguła Sturges jest powszechnie stosowana, ponieważ przybliżenie liczby klas, które zwykle wynosi od 5 do 15.

W ten sposób rozważa wartość, która właściwie reprezentuje próbkę lub populację; To znaczy, podejście nie reprezentuje grup ekstremalnych, ani nie działa z nadmierną liczbą klas, które nie pozwalają na podsumowanie próbki.

Może ci służyć: przeciwległe kątowe przez wierzchołek (z rozwiązanym ćwiczeniem)

Przykład

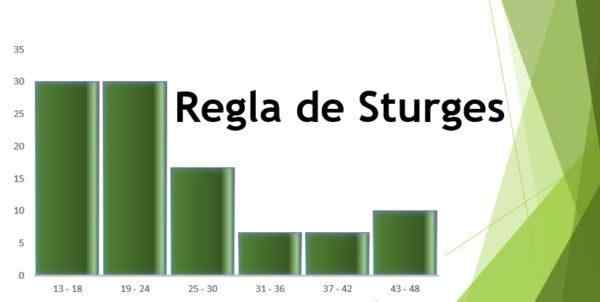
Histogram częstotliwości należy przeprowadzić zgodnie z danymi danymi, które odpowiadają wiekom uzyskanym w badaniu mężczyzn, którzy ćwiczą w lokalnym gimnazjum.

Aby określić interwały, należy znać wielkość próbki lub liczbę obserwacji; W takim przypadku jest ich 30.

Następnie stosuje się zasada Sturges:

K = 1 + 3322 _* dziennik₁₀ (N)

K = 1+3322_* Log (30)

K = 1+3322_* 1 4771

K = 5,90 ≈ 6 przedziałów.

Z liczby przedziałów możesz obliczyć amplitudę, którą będą mieć; to znaczy szerokość każdego słupka reprezentowana w histogramie częstotliwości:

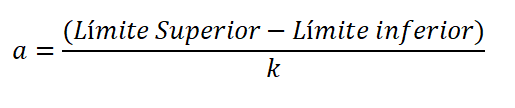
Dolna granica jest uważana za niższą wartość danych, a górna jest najwyższa wartość. Różnica między górną i dolną granicą nazywa się zakresem lub trasą zmiennej (r).

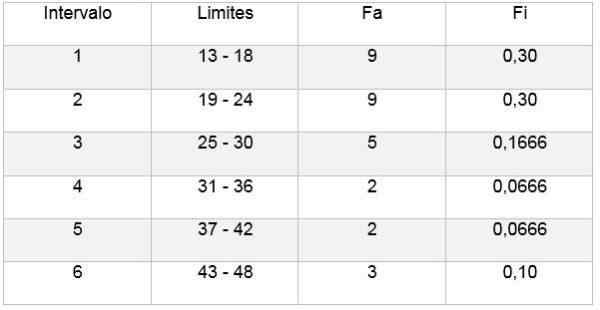
Tabela ma, że ​​górna granica wynosi 46, a dolna 13; W ten sposób amplituda każdej klasy będzie:

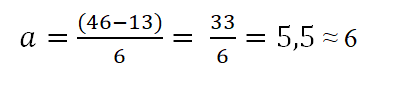
Interwały będą składać się z górnej i dolnej granicy. Aby określić te przedziały, zaczyna się od zliczenia od dolnej granicy, dodając do tego amplitudę określoną przez zasadę (6), w następujący sposób:

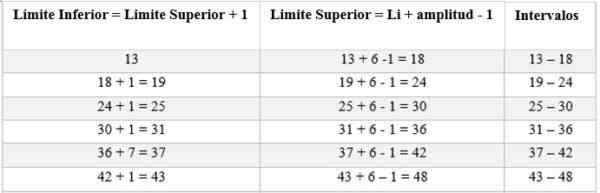
Następnie obliczono częstotliwość bezwzględną w celu określenia liczby mężczyzn odpowiadających każdemu przedziałowi; W takim przypadku jest to:

• Odstęp 1: 13 - 18 = 9
• Odstęp 2: 19 - 24 = 9
• Odstęp 3: 25 - 30 = 5
• Odstęp 4: 31 - 36 = 2
• Odstęp 5: 37 - 42 = 2
• Odstęp 6: 43 - 48 = 3

Dodając bezwzględną częstotliwość każdej klasy, musi to być równe całkowitej liczbie próbki; W tym przypadku 30.

Może ci służyć: negatywna homotecia

Następnie oblicza się względną częstotliwość każdego przedziału, dzieląc bezwzględną częstotliwość tego przez całkowitą liczbę obserwacji:

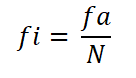
• Odstęp 1: FI = 9 ÷ 30 = 0,30
• Odstęp 2: FI = 9 ÷ 30 = 0,30
• Odstęp 3: FI = 5 ÷ 30 = 0,1666
• Odstęp 4: FI = 2 ÷ 30 = 0,0666
• Odstęp 5: FI = 2 ÷ 30 = 0,0666
• Odstęp 4: FI = 3 ÷ 30 = 0,10

Następnie możesz stworzyć tabelę odzwierciedlającą dane, a także schemat z częstotliwości względnej w stosunku do uzyskanych przedziałów, jak widać na poniższych obrazach:

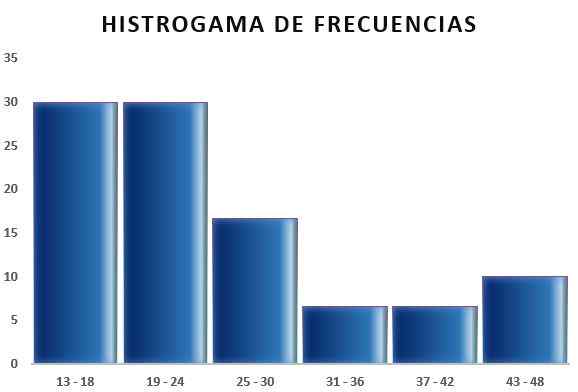
W ten sposób reguła Sturges pozwala określić liczbę klas lub odstępów, w których próbka można podzielić, aby podsumować próbkę danych poprzez opracowanie tabel i grafiki.