Reguła dźwigni

Jaka jest zasada dźwigni?

Reguła dźwigni Jest to procedura matematyczna, która pozwala obliczyć ułamki, procent lub ilości faz obecnych w równowadze w systemie binarnym. Jest to nie tylko matematyczne, ale także dość graficzne i asertywne, jest bardzo przydatne w obliczeniach fizykochemicznych i inżynierskich.

Ta zasada dotyczy diagramów fazowych dla systemów binarnych, niezależnie od rodzaju samego systemu. Oznacza to, że fazy mogą być solidne, jak w przypadku stopów; lub ciekłe i gazowe, jak widzimy w układach w równowadze ciekłoboczkowej.

Fizyczna i matematyczna zasada dźwigni jest również wykorzystywana do celów chemicznych i w fizyce materiałów. Źródło: Jimbowley, CC BY-SA 3.0, Via Wikimedia Commons

Regułę dźwigni można zastosować bezpośrednio, biorąc pod uwagę wartości graficzne w osi odciętej, w których globalne frakcje lub odsetek najbardziej lotnego składnika zwykle idą, w przypadku cieczy; lub oporne, w przypadku metali w ich stopach.

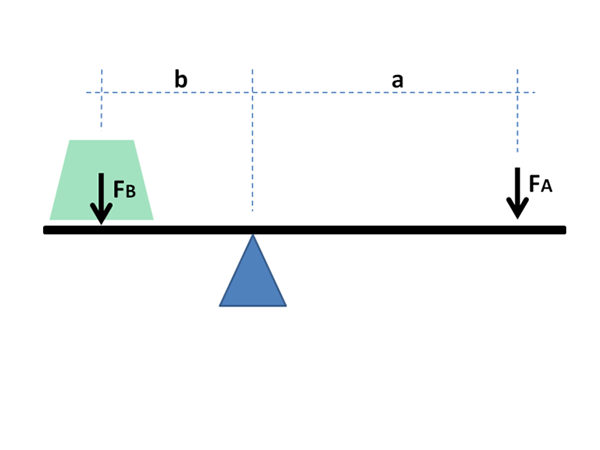
Jak widać poniżej, jego nazwa wynika z ogromnego podobieństwa z wyrażeniami matematycznymi, które pokazują równowagę między dwiema masami znajdującymi się na końcach rockera z Fulcro.

Ramiona dźwigni muszą zrównoważyć, aby zrównoważyć masy obciążeń; W przypadku diagramów fazowych frakcje i mole faz w równowadze materiału.

Wyjaśnienie

Aspekty graficzne

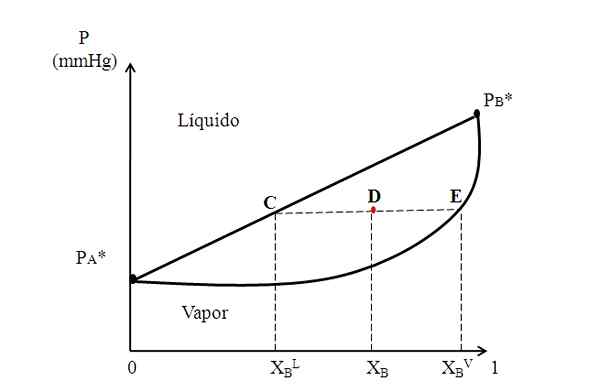Hipotetyczny schemat binarny, w którym linia wiązania pokazuje skład faz cieczy i parowych. Źródło: Gabriel Bolívar.

Na środku powyższego schematu mamy region, w którym ciek i pary współistnieją; to znaczy region równowagi ciekłej-prądowej. Powyżej tego regionu mieszanina A i B będzie płynna, a pod spodem będzie soda z powodu niższych ciśnień.

Teraz rozważ mieszaninę ze składem x_B i którego ciśnienie jest pozycjonowane w punkcie D. Rysujemy z punktu d poziomą linię, która dotyka linii i krzywej po bokach, odpowiednio, pochodzącymi z punktów C i. Ta linia, która komunikuje punkty C, D i E, C-D-E, jest znaną jako linia Unii, a poprzez rzutowanie jej w kierunku osi i musi dać nam presję systemu.

Może ci służyć: alkaliczność wodna: co to jest, determinacja i znaczenie

Następnie z tych punktów rysujemy inne linie prostopadłe do linii wiązania, która będzie grała w osi x. Gdy punkt E spoczywa na krzywej pary, będziemy mieli frakcję molową B w fazie pary (x_B^V). Podobnie punkt C, na prostej linii cieczy, da nam frakcję molową B w fazie ciekłej (x_B^L).

Reguła dźwigni opiera się dokładnie na linii wiązania, a odległości między x_B^L, X_B i x_B^V.

Odliczenie matematyczne

Globalny frakcja trzonowa B jest równa:

X_B = N_B / (N^L + N^V)

Gdzie N_B Są to całkowite mole B zarówno w fazie ciekłej, jak i pary, oraz N^L I N^V są odpowiednie mole dla tych faz. Clearing N_B będziemy mieli:

N_B = X_BN^L + X_BN^V (1)

Z drugiej strony, N_B Jest również równy:

N_B = N_B^L + N_B^V

= X_B^LN^L + X_B^VN^V  (2)

Teraz wyrównujące równania (1) i (2) dadzą nam:

X_BN^L + X_BN^V = X_B^LN^L + X_B^VN^V

I zmienił:

N^L(X_B - X_B^L) = N^V(X_B^V - X_B) (3)

N^L(C-D) = N^V(Z)

Te dwa ostatnie wyrażenia matematyczne są zasadą dźwigni. Zauważ, że x_B - X_B^L Jest to odległość między punktami C i D; i x_B^V - X_B, Jest to odległość między punktami D-E: dwie połowy linii wiązania (ramiona dźwigni).

To równanie jest bardzo podobne do opisu równowagi mas na rockerze z Fulcro:

M₁L₁ = m₂L₂

Zatem reguła dźwigni pozwoli nam obliczyć całkowitą mole N^L I N^V pod warunkiem, że łączne mole mieszaniny są znane, N_T (N_T = N^L + N^V).

Druga forma

Poprzednie wyrażenie reguły dźwigni służy do obliczenia ilości (masy, mole itp.) faz w równowadze. Jednak najbardziej znana wersja reguły dźwigni pozwala nam obliczyć ułamki lub procent każdej fazy, przyjmując tylko odległości między x_B, X_B^L i x_B^V.

Rozważ ten sam system powyżej, mając inną formę zasady dźwigni:

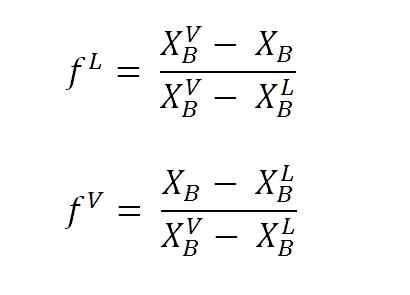Równania do obliczania frakcji cieczy i parowych za pomocą ramion dźwigni. Źródło: Gabriel Bolívar.

Gdzie F ^L I F ^VSą to frakcje molowe (lub procent, w zależności od wykresu) odpowiednio faz cieczy i pary. Zauważ, że oczywiście, F ^L I F ^V Nie mają jednostek; chwila N^L I N^V Tak, mają jednostki (mole, gramy itp.).

Może ci służyć: ciepło reakcyjne

Przykłady

Metoda 1

W pojemniku 28 moli B i 12 moli A są mieszane. Określ ilości i frakcje molowe dla tworzonych faz.

Obliczamy x_B:

X_B = (28 moli b)/ (28 moli b + 12 moli a)

= 0.7

Ta wartość odpowiada x_B górnego schematu. Przechwyty dają nam w przybliżeniu następujące wartości dla x_B^L i x_B^V:

X_B^L = 0.41

X_B^V = 0.94

Z zasadą dźwigni:

N^L(X_B - X_B^L) = N^V(X_B^V - X_B)

I wiedząc o tym N_T = N^L + N^V, I? N_T = 40 moli, a potem oczyszczamy N^L albo N^V w zależności od drugiego:

N^L(X_B - X_B^L) = (40 moli - N^L) (X_B^V - X_B)

Przegrupowanie i usuwanie N^L będziemy mieli:

N^L = (40 moli) (x_B^V - X_B) / (X_B^V - X_B^L)

Czy to wyrażenie nie pamięta tego F ^L? Teraz zastąpimy:

N^L = (40 moli) (0.94 - 0.70) / (0.94 - 0.41)

= 18.11 moli w fazie ciekłej

Możemy obliczyć N^V Na dwa sposoby:

N^V = N^L(X_B - X_B^L) / (X_B^V - X_B)

albo

N^V = 40 moli - 18.11 moli

= 21.89 moli w fazie pary

Metoda 2

Co jeśli obliczymy najpierw F ^L I F ^V?

F ^L = (X_B^V - X_B) / (X_B^V - X_B^L)

= (0.94 - 0.70) / (0.94 - 0.41)

= 0.4528 lub 45.28%

To znaczy 45.2% moli znajduje się w fazie ciekłej, która jest taka równa:

N^L = F ^LN_T

= (0.4528) (40 moli)

= 18.11 moli

I F ^V Możemy obliczyć to jednakowo na dwa sposoby:

F ^V = 1 - F ^L

albo

F ^V = (X_B - X_B^L) / (X_B^V - X_B^L)

Będąc jego wartością:

F ^V = 0.5472 lub 54.72%

I dlatego, N^V Będzie to równe:

N^V = F ^VN_T

= (0.5472) (40 moli)

= 21.89 moli

Zauważ, że zastosowanie dwóch form reguły dźwigni jako alternatywnych metod obliczeń można osiągnąć te same wyniki. Metoda 2 wydaje się bardziej bezpośrednia i prosta; Ale jeśli jest to obserwowane ostrożnie, po rozwiązaniu wyczyszczenia N^L albo N^V, Okaże się, że obie metody są w rzeczywistości równie łatwe.

Rozwiązane ćwiczenia

Następnie zostaną rozwiązane dwa inne ćwiczenia, w których rozważane systemy będą obejmować ciekłokrotny i nie-cieczowy. Również diagramy są graficzne w odniesieniu do temperatury systemu, a nie na ich ciśnieniu.

Ćwiczenie 1

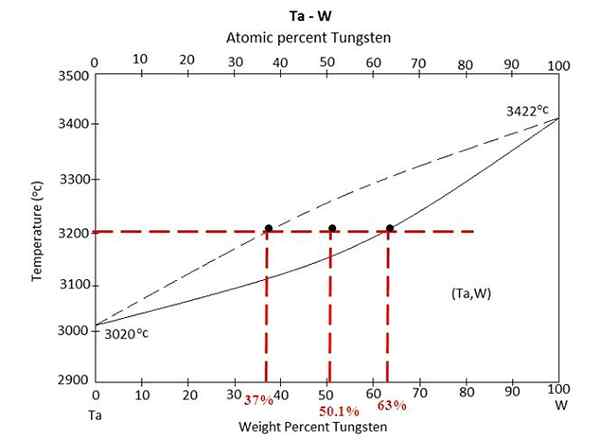Schemat fazowy stopu między tantalo i wolframem. Źródło: Materialsedia, CC BY-SA 4.0, Via Wikimedia Commons

Mamy schemat fazowy powyżej stopu między tantalo i wolframem, TA-W. Na osi x reprezentowane są globalne masowe odsetki wolframu, W% (m/m).

W obrębie regionu równowagi ciekłej (TA+W) i stałym (stopu) występuje mieszanina w temperaturze 3200 ° C. Określ masy każdej fazy, zakładając, że 100 gramów stopu zostało podgrzanych.

Może ci służyć: metale, nie -metal i metaloidy

Procedura

Tym razem ćwiczenie zostanie rozwiązane przy użyciu drugiej formy reguły dźwigni. Linia Unii mówi nam, że: W fazie stałej mamy 63% wolframu, podczas gdy w fazie ciekłej mamy 37% wolframu. Wynika to z faktu, że wolfram topi się w wyższej temperaturze (3422 ° C) niż tantal (3020 ° C).

Więc mamy:

W%^S lub w_S= 63%

W%^L lub w_L= 37%

I również:

W₀ = 50.1%

Stosujemy zasadę dźwigni F ^L:

F ^L = (63% - 50.1%) / (63% - 37%)

= 0.4961 lub 49.61%

Należy zauważyć, że odległość odpowiadająca fazie ciekłej jest ramieniem dźwigni w pobliżu fazy stałej, po przeciwnej stronie punktu średniej.

Masa fazy ciekłej jest zatem:

(0.4961) (100 gramów) = 49.61 stopione gramy

A faza stała będzie równa:

100 gramów - 49.61 gramów = 50.39 gramów stopu bogatego w wolfram

Ćwiczenie 2

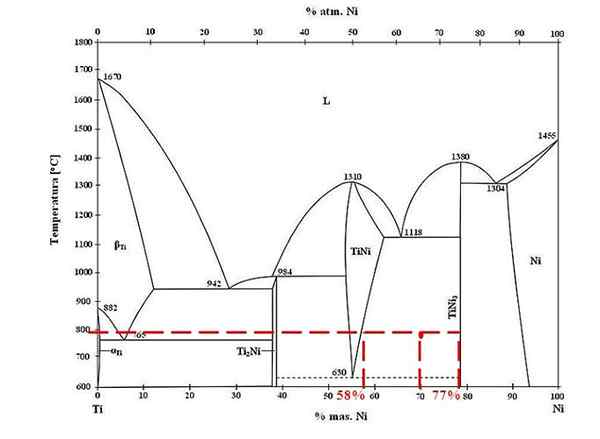Schemat fazowy stopów tytanowych. Źródło: Doomgiver, CC BY-SA 3.0, Via Wikimedia Commons

W przypadku stopu tytanu i niklu w temperaturze 800 ° C, a z 70% nikiel₃ Są obecne.

Procedura

Tym razem proszą tylko o frakcje masowe każdej fazy. Czerwony punkt znajduje się w obszarze równowagi między fazami tini i tini₃, którego krzywe znajdują się tam, gdzie odgrywa linię unii, która przepływa do wartości 58% lub dla fazy tini i 77% lub dla fazy tini₃.

Zauważ, że czerwony punkt jest bliżej fazy Tini₃ z fazy tini. Oznacza to, że musi być więcej tini₃ ten tini; A zatem odległość lub ramię dźwigni odpowiadające tini₃ Musi być najdłuższy, odwrotny (70%-58%).

Wiedząc o tym, przystępujemy do obliczania F ^Tini3:

F ^Tini3 = (70% - 58%) / (77% - 58%)

= 0.6316 lub 63.16%

Rzeczywiście, 63.16% stopu odpowiada fazie tini₃. Tymczasem faza TINI odpowiada:

1 = F ^Tini3 + F ^Tini

F ^Tini = 1 - F ^Tini3

= 0.3684 lub 36.84%

Podsumowując podniesione ćwiczenia, możemy powiedzieć, że zasada dźwigni jest bardzo pomocna w określeniu ułamków każdej fazy w równowadze dla systemu dwuoskładnikowego.

Bibliografia

1. Walter J. Moore. (1963). Chemia fizyczna. W kinetyce chemicznej. Czwarta edycja, Longmans.
2. Iran. Levine. (2009). Zasady fizykochemii. Szósta edycja. MC Graw Hill.
3. Wikipedia. (2020). Reguła dźwigni. Źródło: w:.Wikipedia.org
4. Michael Adewumi. (18 maja 2020). Zasada dźwigni. Odzyskane z: eng.Librettexts.org
5. Adam Warren. (1997). Schematy fazowe: linie remisowe i zasada dźwigni. Odzyskane z: Southampton.AC.Wielka Brytania
6. Uniwersytet Cambridge. (2020). Zasada dźwigni. Źródło: doitpoms.AC.Wielka Brytania