Reaktywność indukcyjna

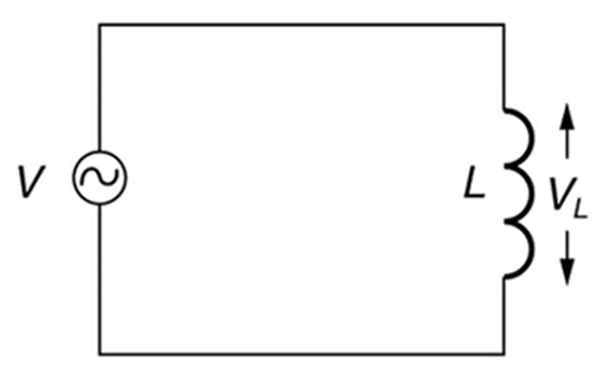
Czysto indukcyjny obwód alternatywny. Źródło: Otwórz STAX. Fizyka uczelni.

Co to jest reaktancja indukcyjna?

Reaktywność indukcyjna Odnosi się do opozycji przedstawionej przez cewkę do przejścia prądu, w alternatywnym obwodzie. Innymi słowy, jest to zdolność induktora do zmniejszenia prądu w alternatywnym obwodzie. Oznaczone jako x_L, Jego wartość zależy od indukcyjności i częstotliwości kątowej napięcia:

X_L= Ω ∙ l

Gdzie ω jest częstotliwością kątową w indukcyjności radian/s, mierzona w Henrios (H) w międzynarodowym systemie jednostek.

Duże indukcyjności wytwarzają dużą reaktancję indukcyjną, ponieważ ich odporność na zmiany jest większa. A reaktancja również wzrasta wraz z częstotliwością, więc pewna indukcyjność L spowoduje większą reaktancję, tym wyższa częstotliwość napięcia.

Jednostką reaktancji indukcyjnej jest Ohmio, symbolizowana przez ω. Jest to ta sama jednostka oporu elektrycznego, ale w przeciwieństwie do tego x_L Nie jest stały, ponieważ zależy od częstotliwości zastosowanego napięcia alternatywnego.

Dlatego w obwodzie, którego jedynymi elementami są alternatywne źródło i indukcyjność (obwód indukcyjny), taki jak ten pokazany na powyższym rysunku, reaktancja indukcyjna będzie zależeć od częstotliwości źródła.

Jednak analogia X_L W przypadku oporu elektrycznego można go rozszerzyć na obwód indukcyjny, umożliwiając zastosowanie prawa Ohma. Jeśli x jest zdefiniowane_L jako stosunek między amplitudami napięcia v_L W indukcyjnym i obecnym i_L To przekracza:

X_L = V_L / SIEMA_L

Możesz napisać prawo Ohm dla obwodów czysto indukcyjnych w następujący sposób:

V_L = X_L∙ i_L

Formuły reaktancji indukcyjnej

Aby obliczyć reaktancję indukcyjną, stosuje się wzór podany na początku, w którym L reprezentuje indukcyjność (Henrios), a ω jest częstotliwością kątową (radian/drugi):

Może ci służyć: Millikan Experiment: Procedura, wyjaśnienie, znaczenie

X_L= Ω ∙ l

Częstotliwość wyrażana jest w Hertz lub Hertzio (HZ). W takim przypadku jest to oznaczone przez F i jest związane z częstotliwością kątową przez wzór:

Ω = 2π ∙ f

W takim przypadku reaktancja jest obliczana jako:

X_L= 2πf ∙ l

W dowolnej z tych wzorów reaktancja indukcyjna powoduje, jak wcześniej wyjaśniono.

Wpływ indukcyjności na obwód indukcyjny

Ponieważ indukcyjność sprzeciwia się zmianom lub zmianom prądu, reaktancja indukcyjna charakteryzuje się opóźnieniem fali prądu w odniesieniu do fali napięcia.

Na poniższym wykresie, który pokazuje napięcie v_L (Niebieski) i obecny i_L (czerwony) W induktor, oba sinoidalnie, obserwuje się, że obie fale są przestarzałe 90º. Począwszy od t = 0, wartość napięcia jest maksymalna, jednak prąd wynosi zero w tym momencie.

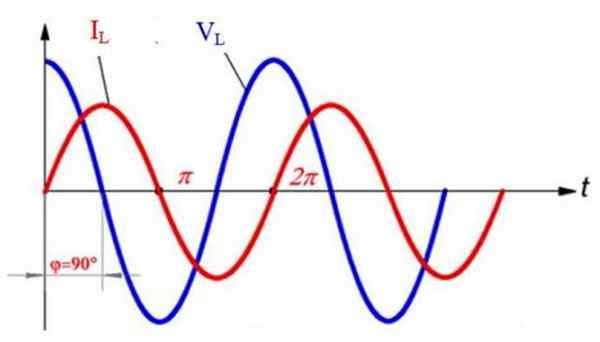Naprzemienny prąd i napięcie w obwodzie indukcyjnym. Przygotowane przez: F. Zapata.

Później obserwuje się, że prąd osiąga maksymalną wartość przy t = π /2, ale do tego czasu napięcie jest anulowane i inwestuje jego polaryzację, to znaczy staje się ujemne. Jednocześnie prąd zmniejsza swoją wartość, podczas gdy napięcie staje się coraz bardziej ujemne.

Następnie, przy t = π, napięcie osiąga maksymalną wielkość, chociaż z odwróconą polaryzacją, a następnie prąd jest anulowany. Z tego wszystkiego wynika, że ​​za każdym razem, gdy v_L Osiąga szczyt, prąd jest anulowany i za każdym razem, gdy prąd osiąga maksymalną wielkość, napięcie wynosi 0.

Prąd zawsze osiąga szczyt po napięciu, a dzieje się tak, ponieważ, jak stwierdzono na początku, indukcyjność sprzeciwia się wzrostowi lub zmniejsza.

Może ci służyć: przewaga mechaniczna: wzór, równania, obliczenia i przykłady

Jak obliczyć reaktancję indukcyjną

Obliczenie reaktancji indukcyjnej jest bardzo proste: konieczne jest znanie wartości indukcyjności i częstotliwości zastosowanego napięcia alternatywnego. Następnie dane te są zastępowane w jednym z formuł podanych w poprzedniej sekcji, a odpowiadająca operacja przeprowadzana jest.

Poniższe przykłady i rozstrzygnięte ćwiczenia pokazują, jak to zrobić w różnych sytuacjach.

Przykłady

Przykład 1

Załóżmy, że L = 5 MH induktor, do którego zastosowano napięcie częstotliwości alternatywnej 60.0 Hz. Reaktancja indukcyjna w tym przypadku jest obliczana przez:

X_L= 2πf ∙ l

Ale przed wymianą wartości indukcyjność musi stać się henrios, mnożąc się przez współczynnik 1 × 10⁻³. Dlatego:

L = 5 × 10⁻³ H

Więc:

X_L= 2πf ∙ l = x_L= 2π × 60 Hz × 5 × 10⁻³ H = 1. 88 Ohm

Przykład 2

Teraz ta sama indukcyjność jest podłączona do innego napięcia częstotliwości alternatywnej: 10.0 kHz. W tym przypadku indukcyjność stanowi większą reaktancję:

X_L= 2πf ∙ l = x_L= 2π × 10.0 × 10³ Hz × 5 × 10⁻³ H = 314.2 Ohm

Przykład 3

Napięcie zastosowane do indukcyjności przykładów 1 i 2 ma wartość 120 V RMS. Odpowiedni prąd RMS jest określany przez OHM V Law_L = X_L∙ i_L:

Siema_L = V_L / X_L

Dla częstotliwości 60.0 Hz, prąd to:

Siema_L = 120 v / 1. 88 OHM = 63.8 a

I dla częstotliwości 10.0 kHz:

Siema_L = 120 v / 314.2 OHM = 0.38 a

Ponieważ w tym drugim przypadku reaktancja jest znacznie większa, oczekuje się, że prąd będzie mniejszy. Ta właściwość sprawia, że ​​induktor jest filtrem wysokiej częstotliwości, funkcją używaną do zmniejszenia dźwięków wysokiej częstotliwości w urządzeniach dźwiękowych lub w celu ochrony urządzeń przed nagłym prądem UPS, między innymi.

Może ci służyć: Twierdzenie Steiner: Wyjaśnienie, aplikacje, ćwiczenia

Rozwiązane ćwiczenia

Ćwiczenie 1

Określić reaktancję indukcyjną w obwodzie, który składa się z indukcyjności 2.5 MH, szeregowo z alternatywnym źródłem napięcia, którego częstotliwość wynosi 75 R.P.M.

Rozwiązanie

Całkowita rewolucja lub cykl równa się 2π radianom, a minuta ma 60 sekund, dlatego częstotliwość 75 r.P.M jest równoważne:

75 r.P.M = 75 × 2π radian / 60 sekund = 7.85 radian/s

I z tą wartością reaktancja to:

X_L= Ω ∙ L = (7.85 radian/s) × 2.5 × 10⁻³ H = 0.02 Ω

Ćwiczenie 2

INDUKCJA SERINALNA jest używana ze źródłem komputera do filtrowania szumu z wysokich częstotliwości.

a) Jaka powinna być minimalna wartość indukcyjności niezbędna do wytworzenia reaktancji 2 kΩ, jeśli częstotliwość sygnału, która ma filtrować wynosi 15 kHz?

b) Znajdź reaktancję tego induktora przy częstotliwości 60 Hz.

Rozwiązanie

X_L = 2 kΩ = 2000 Ω

F = 15 kHz = 15000 Hz

Dlatego wyczyszczenie równania x_L= 2πf ∙ l, masz:

L = x_L / 2π ∙ f = 2000 Ω / 2π × 15000 Hz = 0.0212 H = 21.2 MH

Rozwiązanie b

Używając ponownie x_L= 2πf ∙ L, ale z F = 60 Hz, wyniki:

X_L= 2π × 60 Hz × 0.0212 H = 8 Ohm.

Bibliografia

1. Bauer, w. (2011). Fizyka inżynierii i nauki. Tom 1. MC Graw Hill. 
2. Giancoli, zm. (2006). Fizyka: zasady z aplikacjami. 6th. Ed Prentice Hall.
3.  Katz, d. (2013). Fizyka dla naukowców i inżynierów. Fundamenty i połączenia. Cengage Learning.
4. Otwórz Stax. Fizyka uczelni. Źródło: OpenStax.org.
5. Sears, z. (2016). Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Głośność 2. osoba