Przyczyny trygonometryczne Przyczyny, ćwiczenia i zastosowania

Przyczyny trygonometryczne Są to iloraz lub powody, które można wykonać z wartością boków prawego trójkąta. Strony te to: dwie kategorie, które tworzą się 90º ze sobą i przeciwprostokątne, które tworzy ostry kąt θ z jedną z kategorii.

Można utworzyć 6 ilorazów. Ich nazwiska i odpowiednie skróty to:

• Brease (Sen)
• Coseno (cos)
• styczna (tg lub tan)
• Cotangent (CTG lub Cotan)
• SECANTE (SEC) i
• Harvester (harmonia)

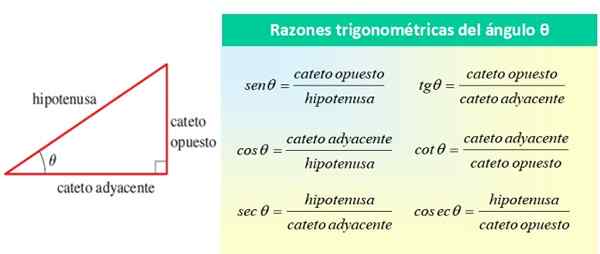
Wszystkie odnosiły się do kąta θ, jak pokazano na poniższym rysunku:

Rysunek 1. Przyczyny trygonometryczne ostrego kąta θ. Źródło: f. Zapata.

Podstawowymi przyczynami trygonometrycznego kąta θ są sin θ, cos θ i tan θ, podczas gdy pozostałe przyczyny można wyrażać w kategoriach tych trzech. Z poprzedniego zdjęcia możesz to zobaczyć:

• Sec θ = 1/ cos θ
• szkoda θ = 1/ sin θ
• COT θ = 1/tg θ

Rozmiar boków trójkąta nie wpływa na wartość przyczyn, ponieważ dwa trójkąty, których kąty mierzą to samo, są podobnymi trójkątami, a odpowiednie iloraz między bokami mają tę samą wartość.

[TOC]

Przykład

Na przykład obliczmy trygonometryczne przyczyny kąta θ w następujących trójkątach:

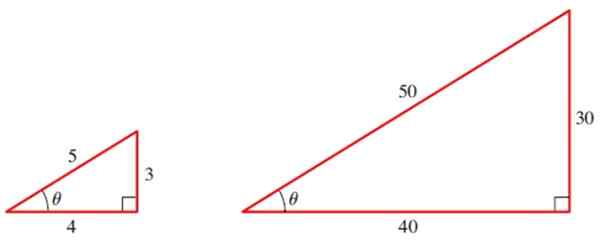Rysunek 2. Dwa podobne trójkąty mają te same trygonometryczne przyczyny ich kąty. Źródło: Stewart, J.Prefrecment: Matematyka do obliczania.

W przypadku małego trójkąta mamy trzy podstawowe przyczyny kąta θ:

sin θ = 3/5

cos θ = 4/5

tg θ = ¾

A teraz obliczmy trzy podstawowe powody θ z dużym trójkątem:

sin θ = 30/50 = 3/5

cos θ = 40/50 = 4/5

Tg θ = 30/40 = ¾

Ważnym szczegółem do rozważenia jest następujący: zarówno sin θ, jak i cos θ są mniejsze niż 1, ponieważ kategorie zawsze mierzą mniej niż hipotencja. Rzeczywiście:

sin θ = 3/5 = 0.6

cos θ = 4/5 = 0.8

Rozwiązane ćwiczenia

W poniższych ćwiczeniach poproszono o rozwiązanie prawego trójkąta, co oznacza znalezienie długości jego trzech stron i miary jego kątów wewnętrznych, z których jeden zawsze mierzy 90º.

Może ci służyć: pierwsze -stope równania: formuła, jak je rozwiązać, przykład, ćwiczenia

Twierdzenie Pitagorasa dotyczy trójkątów prostokątnych i jest bardzo przydatne, gdy znane są dwie strony. Twierdzenie mówi:

Przeciwprostokątna² = przeciwny Cateto² + sąsiednie Cateto²

Możemy zweryfikować twierdzenie Pitagorasa z małym trójkątem na ryc. 2, którego nogi wynoszą 3 i 4. Kolejność, w której kategorie są pobierane, nie ma znaczenia. Stosując, że mamy:

Przeciwprostokątna² = 3² + 4² = 9 + 16 = 25

Dlatego przeciwprostokątna jest:

Hipotenuse = √25 = 5

- Ćwiczenie 1

Oblicz przyczyny trygonometryczne kąty pokazanych w następujących trójkątach:

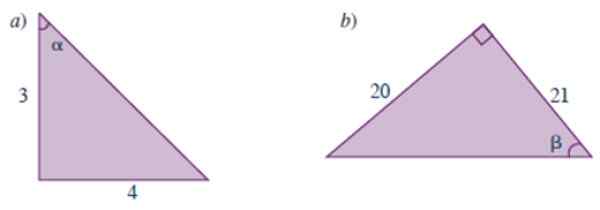Rysunek 3.- Trójkąty za rok rozwiązały 1. Źródło: Carena, m. 2019. Podręcznik matematyki przednicznicy.

Rozwiązanie

Ten trójkąt jest taki sam na rycinie 3, ale pytają nas o powody trygonometryczne drugiego ostrego kąta, oznaczonego α. Oświadczenie nie oferuje jednak wartości hipotenu, stosując twierdzenie Pitagorasa, wiemy, że jest warte 5.

Przyczyny można obliczyć bezpośrednio na podstawie definicji, zachowując ostrożność przy wyborze nogi, która jest przeciwieństwem kąta α w celu obliczenia SEN α. Zobaczmy:

• sin α = 4/5
• cos α = 3/5
• TG α = 4/3
• COT α = ¾
• Sec α = 1/(3/5) = 5/3
• szkoda α = 1/(4/5) = 5/4

I jak widzimy, wymieniono wartości przyczyn trygonometrycznych. Rzeczywiście, α i θ są kątami uzupełniającymi, co oznacza, że ​​dodają 90º. W takim przypadku jest spełnione, że Sen α = cos θ i tak dalej z innych powodów.

Rozwiązanie b

Obliczmy hipotencję trójkąta przez twierdzenie Pitagorasa:

Przeciwprostokątna² = 20² + dwadzieścia jeden² = 841

√841 = 29

Następnie 6 trygonometrycznych przyczyn kąt β to:

• Sen β = 20/29
• cos β = 21/29
• TG β = 20/21
• COT β = 21/20
• Sec β = 1/(21/29) = 29/21
• szkoda β = 1/(20/29) = 20/29

Może ci służyć: połączone operacje

- Ćwiczenie 2

a) Znajdź wartość x na rysunku.

b) Obliczyć obwód 3 pokazanych trójkątów.

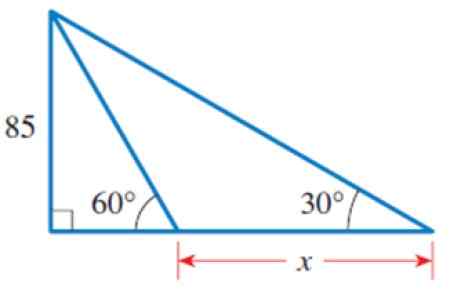Rysunek 4. Trójkąty za rok rozwiązały 2. Źródło: Stewart, J. Prefrecment: Matematyka do obliczania.

Rozwiązanie

Na rysunku możemy zidentyfikować kilka trójkątów, w szczególności trójkąt prostokąta po lewej, który ma kategorię równą 85 i ostry kąt 60º.

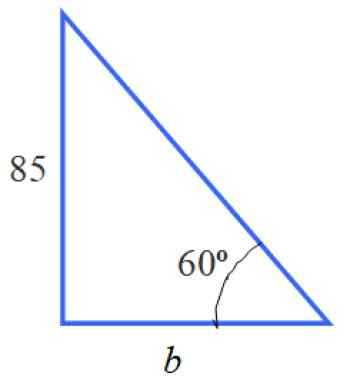Rysunek 5. Trójkąt po lewej stronie.

Z informacją o tym trójkącie możemy obliczyć stronę B. Nie jest to miara, o którą pyta stwierdzenie, ale znajomość jego wartości jest poprzednim krokiem.

Aby ustalić odpowiedni powód, jest TG 60 ° = 85 /B, ponieważ B jest nogą przylegającą do 60 °, a 85 jest przeciwne do wspomnianego kąta. Dlatego:

B = 85 / TG ​​60º = 85 / √3

Kiedyś znamy B, użyjemy dużego i zewnętrznego trójkąta prostokąta, który ma wspólną stronę z poprzednim trójkątem: ten, który mierzy 85. To jest cateto przeciwne kątowi 30º.

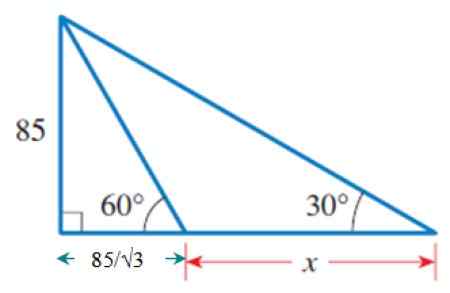Rysunek 6. Zewnętrzny trójkąt, z którego część podstawy jest już znana.

Stamtąd:

Cateto sąsiadujący z 30º = (85/√3) + x

Teraz możemy podnieść następujące czynności:

85 / [(85 / √3) + x] = tg 30º

Co jest w nawiasach kwadratowych mnożą 30º TG:

85 = [(85/√3) + x]. TG 30º

Zastosowanie właściwości dystrybucyjnej mnożenia:

85 = TG 30º. (85/√3) + x. TG 30º

Dlatego:

X.TG 30º = 85 - TG 30º. (85/√3) = 85 [1 - TG 30º . (1/√3)] = 85 . (2/3) = 170/3

Zastąpienie wartości TG 30º = √3 / 3:

x = (170/3) ÷ (√3 / 3) = 98.piętnaście

Rozwiązanie b

Obwód małego trójkąta

Być h₁ Hipotenuse tego trójkąta, które można obliczyć za pomocą twierdzenia Pitagorasa lub z powodu trygonometrycznego, na przykład COS 60º:

COS 60 ° = 85 / √3 / h₁→ H₁ = (85/√3) ÷ cos 60º = 98.1

Aby znaleźć P, obwód tego trójkąta, po prostu dodajemy 3 strony:

Może ci służyć: statystyka opisowa: historia, cechy, przykłady, koncepcje

P = 85 + (85/√3) + 98.1 = 232.2

Obwód trójkąta zewnętrznego

Być h₂ do hipotenu zewnętrznego trójkąta:

Sen 30º = 85 ÷ h₂  

H₂ = 85 ÷ sin 30º = 170

W tym trójkącie obwód jest:

P = 85 + [(85/√3) + 98.15] + 170 = 402.22

Obwód trójkąta bezrektanżowego

Z tego trójkąta znamy już wszystkie jego strony:

P = x + h₁ + H₂ = 98.15 + 98.15 + 170 = 366.3

Zastosowania przyczyn trygonometrycznych

Przyczyny trygonometryczne mają wiele praktycznych zastosowań, na przykład można obliczyć wysokości.

Załóżmy, że wieża wodna ma 325 stóp od budynku. Obserwator zlokalizowany w oknie, zauważa, że ​​kąt wysokości górnego końca wieży wynosi 39 °. Cuda:

a) Jaka jest wysokość wieży?

b) Ile kosztuje okno?

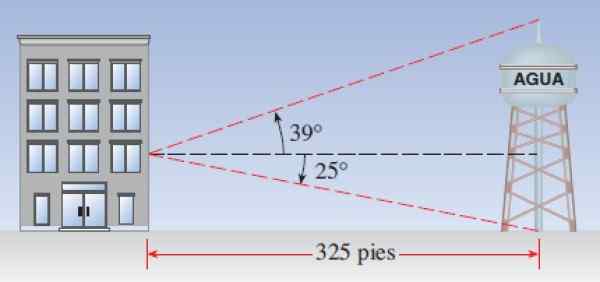Rysunek 7. Plan obliczenia wysokości Vista Torre z budynku. Źródło: Stewart, J. Prefrecment: Matematyka do obliczania.

Rozwiązanie

Od Cateto naprzeciwko 39 górnego trójkąta otrzymujemy część odpowiedzi:

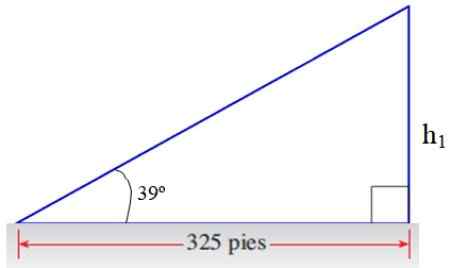Cyfra 8. Trójkąt do ćwiczeń aplikacyjnych. Źródło: f. Zapata.

H₁/325 = TG 39º → H₁ = 325 . TG 39º stóp = 263.2 stopy

W podobny sposób otrzymujemy resztę wysokości wieży, zwanej h₂ Z niższego trójkąta:

H₂/325 = TG 25º → H₂ = 325 . TG 25º stóp = 151.6 stóp

Całkowita wysokość wieży wynosi h₁ + H₂ = 263.2 + 151.6 stóp = 414.7 stóp.

Rozwiązanie b

Okno jest dokładnie na wysokości h₂ grunt:

H₂ = 151.6 stóp.

Bibliografia

1. Carena, m. 2019. Podręcznik matematyki przednicznicy. National University of the Coast.
2. Hoffman, J. Wybór problemów z matematyką. Tom 3.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Stewart, J. 2006. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.
5. Zill, d. 1984. Algebra i trygonometria. McGraw Hill.