Definicja radia konwergencji, przykłady i ćwiczenia

On Promień konwergencji serii mocy jest promień kręgu konwergencji, do którego zbiega się seria. Ten okrąg rozciąga się od wartości, która anuluje podstawę mocy do najbliższej osobliwości funkcji związanej z serią.

Cała funkcja analityczna F z) Powiązał szereg mocy wokół punktu nieingowego, zwanego Seria Taylor:

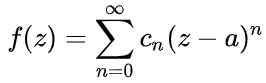
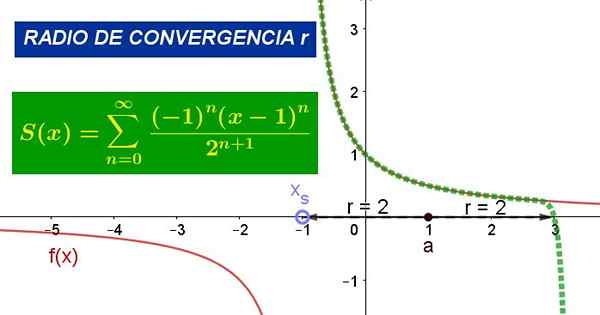
Rysunek 1. Wykres pokazuje serię mocy wokół wartości a = 1 dla funkcji f (x). Jego promień zbieżności wynosi r = 2. Źródło: Fanny Zapata.

Gdzie Do Jest to centrum kręgu konwergencji, z niezależna zmienna funkcji i C_N Są to współczynniki związane z tymi uzyskanymi z funkcji F o punkcie Z = a.

Promień konwergencji R Jest to dodatnia liczba rzeczywista, która określa region:

| Z - a | < r

Gdzie zbiega się seria. Z tego regionu seria rozbieżnej, to znaczy wymaga nieskończonych wartości. Gdy promień zbieżności jest nieskończony, wówczas seria zbiega się w całej płaszczyźnie złożonej.

[TOC]

Jak określa się promień konwergencji?

Aby seria była zbieżna, konieczne jest, aby wartość bezwzględna kolejnych terminów spadła, gdy liczba terminów jest bardzo duża. W sposób matematyczny byłby wyrażony w następujący sposób:

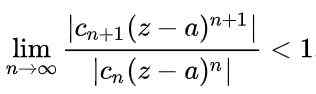
Uzyskuje się to właściwości granic w poprzednim wyrażeniu:

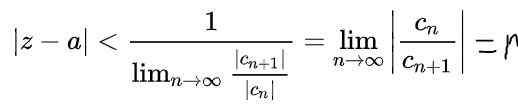
Tutaj R Jest to promień konwergencji i | Z - a | < r Jest to otwarty okrąg graniczny w złożonej płaszczyźnie, w której zbiega się seria. W przypadku wartości Do a zmienna Z to liczby rzeczywiste, wówczas otwarty odstęp zbieżności na prawdziwej osi będzie: (A - r, a+r).

Seria Taylor

Seria funkcji Taylor f (x) Wokół wartości Do W którym funkcja ma nieskończone pochodne, jest to seria mocy zdefiniowanej jako:

Może ci służyć: aksjomaty prawdopodobieństwa: typy, wyjaśnienie, przykłady, ćwiczenia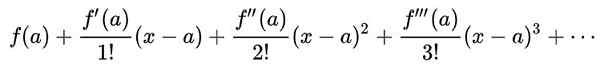

W otoczeniu |. X - A | < r, z R JakPromień konwergencji serii, seria Taylor i funkcja muszą być f (x) Zbieżą się.

Z drugiej strony promień konwergencji R Jest to odległość punktu Do i osobliwość X_S bliżej rzeczy Do, będąc punktami liczbowymi tymi wartościami, w których granica funkcji ma tendencję do nieskończoności.

To jest, kiedy x → x_S Więc F → ± ∞.

Przykłady

Przykład 1

Być S (x) Moce podane przez następujące wyrażenie:

S (x) = 1 - x + x²- X³+ X⁴-.. .+(-1)^N ⋅ x^N +.. .

Aby określić region, w którym zbiega się seria, obliczamy iloraz między terminem (n-beeimo + 1) a terminem (n-em):

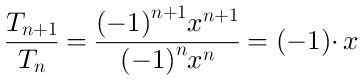
Wartość bezwzględna ilorazu przedniego jest | x | i jego limit, kiedy N → ∞ to jest również  | x |.

Aby seria była zbieżna, konieczne jest:

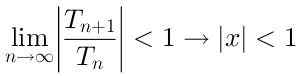
Tak więc promień konwergencji tej serii jest R = 1, ponieważ zbiega się dla wartości x, które są w odległości mniejszej niż 1 w odniesieniu do środka x = 0.

Przykład 2

Chcesz znaleźć serię funkcji Taylor f (x) = 1 / (1 + x) wokół punktu x = 0 i określ jego promień zbieżności.

Aby znaleźć serię, przyjmujemy kolejne pochodne funkcji F (x), z których pokażemy pierwsze trzy:

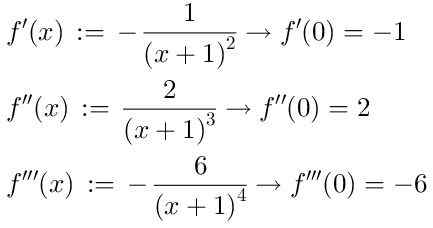
Biorąc pod uwagę, że termin zero zamówienia serii Taylor jest:

 f (0) = 1,

Pierwsze zamówienie: F '(0)/1!

Drugie zamówienie:

 F "(0)/2!

Trzecie zamówienie:

 f "(0)/3!

I tak dalej, seria Taylor danej funkcji to:

f (x) = 1 - x + x² - X³ + X⁴ -.. .+(-1)^N ⋅ x^N +.. .

Może ci służyć: trójkąt równoboczny: Charakterystyka, właściwości, wzory, obszar

Co zbiega się z serią mocy badaną w przykładzie 1.

Powiedzieliśmy już, że promień konwergencji serii Taylor to odległość od centrum rozszerzenia w szeregu, co w naszym przypadku jest wartością x = 0 aż do pierwszej osobliwości funkcji f (x). 

Ponieważ nasza funkcja ma osobliwość (to znaczy nieskończoność) x = -1, Odległość między wartością -1 i centrum ekspansji 0 Jest | -1 - 0 | = 1, Stwierdzono, że promień konwergencji serii Taylor jest 1.

Wynik ten całkowicie pokrywa się z tym uzyskanym w przykładzie 1 inną metodą.

Fakt, że strefa konwergencji serii Taylor jest przedziałem otwartym (-1, 1), oznacza, że ​​funkcja i seria pokrywają się w tym przedziale, ale nie są poza tym samym.

To pokazano na rycinie 2, gdzie pobrano 41 terminów serii Taylor, narysowane przez ciągłą niebieską linię, podczas gdy pierwotna funkcja jest pokazana na czerwonej linii segmentów.

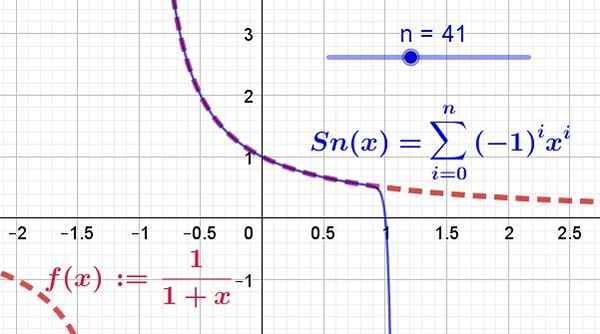Rysunek 2. Pokazano funkcję f (x) (na czerwono) i jej seria mocy (lub seria Taylor w kolorze niebieskim). Można go postrzegać jako pierwsze 41 warunków serii zbiegają się między -1 a 1. Ponadto funkcja i jej seria pokrywają się tylko w regionie konwergencji. (Źródło: Fanny Zapata)

Rozwiązane ćwiczenia

- Ćwiczenie 1

Rozważ tę samą funkcję f (x) = 1 / (1 + x) przykładu 2, ale tym razem wymaga się znalezienia serii Taylor wspomnianej funkcji wokół punktu a = 1.

Rozwiązanie

Znajdujemy kolejne warunki serii, zaczynając od niezależnego terminu, czyli f (1) = ½.

Kolejnym współczynnikiem odpowiadającym terminowi pierwszego rzędu jest:

F '(1)/1! = -¼

Drugie zamówienie to:

f "(1)/2! = 2/(2³ 2!)

Postępuj zgodnie z współczynnikiem trzeciego rzędu:

Może ci służyć: tetradecágon

f "(1)/3! = -6 / (2⁴ 3!)

I tak dalej. Seria Taylor będzie:

SF (x) = ½ - 1/2² (X-1) + 1/2³(X-1)² - 1/2⁴ (X-1)³ + 1/2⁵ (X-1)⁴-..

- Ćwiczenie 2

Znajdź promień zbieżności z poprzedniej serii

Rozwiązanie

Piszemy termin n-em i termin n-alkaus więcej:

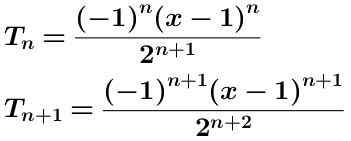Obliczamy iloraz tych dwóch terminów, które pokazano poniżej uproszczonego:

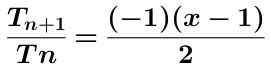
Wartość bezwzględna poprzedniego wyrażenia jest przyjmowana poprzez uzyskanie:

|. X - 1 | / 2

Jednak aby seria była zbieżna, konieczne jest, aby poprzednia kwota była ściśle niższa niż jednostka, to znaczy:

|. X - 1 | < 2

Co wskazuje, że promień zbieżności wokół wartości x = 1 wynosi:

R = 1

Z drugiej strony poprzednie wyrażenie jest równoważne z podwójną nierównością:

-2 < x - 1 < +2

Jeśli dodamy +1 do każdego z trzech członków poprzedniego wyrażenia, zostanie ono uzyskane:

-1 < x < 3

Który jest serią konwergencji.

Rysunek 1 pokazuje oryginalną funkcję i serię wspomnianej funkcji Taylor wokół punktu x = 1. Na rysunku można zweryfikować, że seria pokrywa się z funkcją w środowisku punktu x = 1, ale w promieniu zbieżności.

Bibliografia

1. Fundacja CK-12. Seria mocy: reprezentacja funkcji i operacji. Odzyskane z: CK12.org.
2. Engler, a. 2019. Rachunek integralny. National University of the Coast.
3. Larson, r. 2010. Obliczanie zmiennej. 9na. Wydanie. McGraw Hill.
4. Darmowe teksty matematyki. Seria Power. Odzyskane z: matematyki.Liibretexts.org.
5. Wikipedia. Seria Power. Odzyskane z: jest.Wikipedia.org.
6. Wikipedia. Promień konwergencji. Źródło: w:.Wikipedia.org