Jaki jest moment magnetyczny?

On Moment magnetyczny Jest to wektor, który dotyczy prądu, który przekracza trochę lub zamkniętą pętlę z obszarem tego samego. Jego moduł jest równy iloczynowi intensywności prądu przez obszar, a jego kierunek i kierunek są podane przez zasadę prawej ręki, jak pokazano na rycinie 1.

Ta definicja jest ważna niezależnie. Jeśli chodzi o jedność momentu magnetycznego, w międzynarodowym systemie jednostek, jeśli jest to ampere × m².

Rysunek 1. Wektor momentu magnetycznego dowolnego wiązania prądu jest prostopadle do jego płaszczyzny, a kierunek jest określany przez prawą zasadę kciuka. Źródło: Wikimedia Commons.

W kategoriach matematycznych oznaczanie wektorowego momentu magnetycznego za pomocą greckich tekstów μ (Bold, ponieważ jest wektorem, a zatem odróżnia się od swojej wielkości), jest wyrażany jako:

μ = IA N

Gdzie i jest intensywnością prądu, a jest obszarem, który otacza pętlę i N To wektor jednostkowy (modułu równego 1) wskazuje w kierunku prostopadłym do płaszczyzny spazu i którego znaczenie jest nadane przez zasadę prawego kciuka (patrz ryc. 1).

Ta zasada jest bardzo prosta: zwinięcie czterech palców prawej ręki, aby podążały za prądem, kciuk wskazuje kierunek i kierunek N a zatem moment magnetyczny.

Poprzednie równanie jest ważne dla pętli. Jeśli istnieją nougas jak w cewce, moment magnetyczny jest mnożony przez n:

μ = nIA N

[TOC]

Moment magnetyczny i pole magnetyczne

Łatwo jest znaleźć wyrażenia dla magnetycznego momentu zakrętów o regularnych kształtach geometrycznych:

-Kwadratowa strona boku ℓ: μ = Iℓ² N

-Boki prostokątna spirala Do I B: μ = IAB N

-Radio R. Radio Spira: μ = Iπr² N

Może ci służyć: liczba atomowa

Pole magnetyczne Dipolo

Pole magnetyczne wytwarzane przez prądową pętlę lub spaz przypomina pole magnesu słupkowego, a także pola Ziemi.

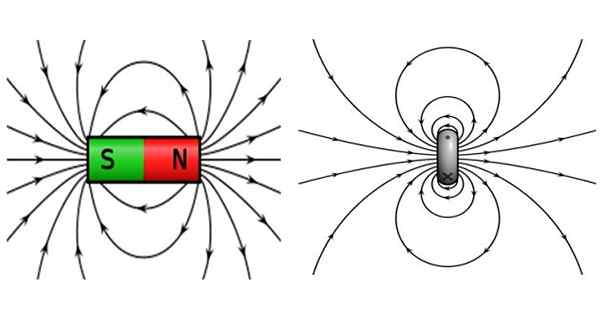Rysunek 2. Po lewej stronie pole magnetyczne magnesu słupkowego i po prawej. Źródło: Wikimedia Commons.

Magnesy słupkowe charakteryzują się posiadaniem bieguna północnego i bieguna południowego, gdzie przyciągane są przeciwne bieguny i odstraszają te same bieguny. Linie pola są zamknięte, opuść biegun północny i dotrzeć do bieguna południowego.

Teraz bieguny magnetyczne są nierozłączne, co oznacza, że ​​jeśli magnes barowy jest podzielony na dwa mniejsze magnesy, nadal mają własne bieguny północne i południowe. Nie jest możliwe posiadanie izolowanych bieguna magnetycznego, dlatego nazywany jest magnes słupkowy Magnetyczny Dipolo.

Pole magnetyczne o promieniu r spiralnym r, które transportuje prąd I, jest obliczane przez prawo biot-savart. Dla punktów należących do osi symetrii (w tym przypadku osi x) pole podaje:

Gdzie μ_albo Jest to przepuszczalność próżni. Zabranie pola w punktach od spazu, dla którego jest spełnione, że X >> R zbliża się pole:

Związek między polem magnetycznym a momentem magnetycznym Dipolo

W tym moment magnetyczny w poprzednim wyrażeniu to:

W ten sposób intensywność pola magnetycznego jest proporcjonalna do momentu magnetycznego. Zauważ, że intensywność pola maleje wraz z kostką odległości.

Takie podejście ma zastosowanie do każdej pętli, o ile X być duży w porównaniu do jego wymiarów.

A ponieważ linie tego pola przypominają linie magnesu słupkowego, równanie jest dobrym modelem tego pola magnetycznego i innych układów, których linie są podobne, takie jak: na przykład:

Może ci służyć: Absorbancja: co jest, przykłady i ćwiczenia rozwiązane

-Cząstki załadowane w ruchu jako elektron.

-Atom.

-Ziemia i inne planety i satelity układu słonecznego.

-Gwiazdy.

Wpływ pola zewnętrznego na pętlę

Bardzo ważną cechą momentu magnetycznego jest jego powiązanie z momentem obrotowym, którego doświadcza pętla w obecności zewnętrznego pola magnetycznego.

Silnik elektryczny zawiera cewki, przez które przechodzi strumień zmieniającego się kierunku, i że dzięki zewnętrznemu pola doświadcza efektu zwrotnego. Ta tura powoduje ruch osi, a energia elektryczna staje się energią mechaniczną podczas procesu.

Moment obrotowy na prostokątnej pętli

Załóżmy, aby ułatwić obliczenia, prostokątne strony Do I B, którego normalny wektor N, wychodzący ekran, początkowo jest prostopadły do ​​jednolitego pola magnetycznego B, jak na rycinie 3. Boki siły doświadczenia w pętli podane przez:

F = IL X B

Gdzie L Jest to wektor wielkości równy długości segmentu i skierowany według prądu i jest intensywnością tego samego i B To pole. Siła jest prostopadła do obu L Jak pole, ale nie wszystkie strony doświadczają siły.

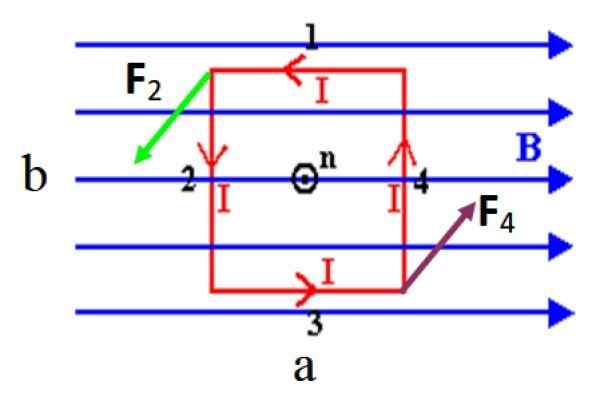Rysunek 3. Prostokątna spirala, która przenosi prąd I w sensie antyhorarycznym, doświadcza momentu obrotowego w obecności jednolitego jednolitego pola magnetycznego. Źródło: f. Zapata.

Na pokazanym rysunku nie ma siły na krótkich stronach 1 i 3 do bycia równoległym do pola, pamiętaj, że produkt krzyżowy między wektorami równoległymi jest nieważny. Jednak długie strony 2 i 4, które są prostopadłe B, Doświadczają, że oznaczają siły jako F₂ I F₄.

Siły te tworzą się para: Mają tę samą wielkość i kierunek, ale przeciwne zmysły, dlatego nie są w stanie przenieść się do pętli na środku pola. Ale mogą to obrócić, ponieważ moment obrotowy  τ Że każda siła wywiera, w odniesieniu do osi pionowej, która przechodzi przez środek pętli, ma ten sam kierunek i znaczenie.

Może ci służyć: siła spójności

Zgodnie z definicją momentu obrotowego, gdzie R Jest to wektor pozycji:

τ = R X F

Więc:

τ₂ = τ₄=(A/2) f (+J )

Poszczególne momenty obrotowe nie są anulowane, ponieważ mają ten sam kierunek i znaczenie, a następnie są dodawane:

τ_internet = τ₂ + τ₄ = F (+J )

I będąc wielkością siły f = IBB, powoduje to:

τ_internet = I⋅A⋅B⋅B (+J )

Produkt A⋅B jest obszarem A Spaza, więc IAB to wielkość momentu magnetycznego μ. Dlatego τ_internet = μ⋅b (+J )

Można zauważyć, że ogólnie moment obrotowy pokrywa się z produktem wektorowym między wektorami μ I B:

τ_internet = μ X B

I chociaż to wyrażenie pochodziło z prostokątnej pętli, jest ono ważne dla płaskiego poziomu.

Wpływ pola na pętlę to moment obrotowy, który ma tendencję do wyrównania momentu magnetycznego z polem.

Energia potencjalna dipola magnetycznego

Aby obrócić spiralę lub dipol na środku pola, należy wykonać pracę przeciwko sile magnetycznej, która zmienia energię potencjalną Dipolo. Zmienność energii δu, gdy spirala obraca się z kąta θ_albo Pod kątem θ jest podawany przez całkę:

Jeśli poziom odniesienia jest wybrany jako θ_albo = π/2:

Δu = -μb cos θ

Co z kolei można wyrazić jako produkt skalarny między wektorami B I μ:

Δu = - μ ·B

Minimalna energia potencjalna w dipole występuje, gdy cos θ = 1, co oznacza to μ I B Są równoległe, energia jest maksymalna, jeśli są przeciwne (θ = π) i są zerowe, gdy są prostopadłe (θ = π/2).

Bibliografia

1. Figueroa, zm. 2005. Seria: Fizyka nauk i inżynierii. Tom 5. Elektromagnetyzm. Pod redakcją Douglas Figueroa (USB).
2. Resnick, r. 1999. Fizyczny. Tom. 2. Wydanie trzecie. po hiszpańsku. Continental Editorial Company S.DO. c.V.
3. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Głośność 2. osoba.
4. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Głośność 2. 7th. Wyd. Cengage Learning.
5. Tipler, str. (2006) Physics for Science and Technology. Ed. Głośność 2. Redakcja Reverted.