Jaki jest moduł cięcia, sztywności lub ścinania? (Rozwiązane ćwiczenia)

On Wytnij moduł Opisz odpowiedź materiału na zastosowanie wysiłku ścinającego, który go deformuje. Inne częste wyznaczenia modułu cięcia to ścinanie, nożyce, elastyczność poprzeczna lub moduł elastyczności stycznej.

Kiedy wysiłki są niewielkie, deformacje są dla nich proporcjonalne, zgodnie z prawem Hooke, a stał. Dlatego:

Moduł cięty = wysiłek cięcia/deformacji

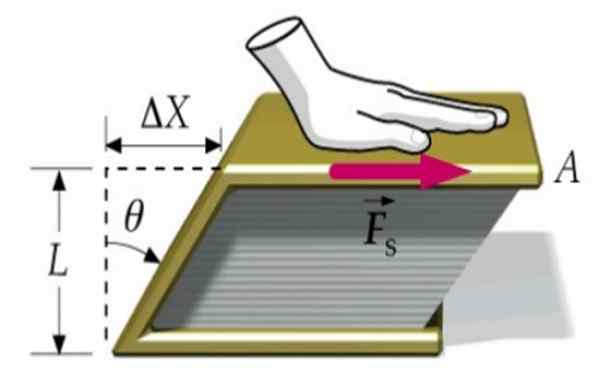
Rysunek 1. Książka jest zdeformowana dzięki stycznej sile FS. Źródło: f. Zapata.

Załóżmy, że na pokrywkę książki nakłada się siłę, będąc drugim przymocowanym na powierzchni tabeli. W ten sposób książka jako całość nie porusza się, ale deformuje się, gdy górna pokrywka porusza się w odniesieniu do dolnej Δx.

Książka przechodzi z prostokątnej sekcji poprzecznej do sekcji w postaci równoległoboku, jak widzimy na obrazie wyższym.

Być:

τ = f/a

Wysiłek lub napięcie cięcia, bycie F wielkość przyłożonej siły i DO Obszar, na którym działa.

Odkształcenie spowodowane jest iloraz:

δ = δx / l

Dlatego moduł tnąca, który będziemy oznaczyć jako G, to:

W ten sposób moduł cięcia jest odpowiedzialny za pomiar odporności wewnętrznych płaszczyzn obiektu, które są równoległe do stosowanego wysiłku.

A ponieważ δx / l nie ma wymiarów, jednostki g są takie same jak w przypadku wysiłku tnącego, co jest przyczyną między siłą a obszarem.

W międzynarodowym systemie jednostek jednostkami te to Newton/Square Metro lub Pascal, skrócone PA. A w jednostkach anglo -saksonów jest to funt /cal kwadratowy, skrócony psi.

[TOC]

Może ci służyć: jednolity ruch prostoliniowy: cechy, wzory, ćwiczenia

Wytnij moduł dla różnych materiałów

Pod działaniem sił tnących, takich jak opisane, obiekty oferują opór podobny do książki, w której warstwy wewnętrzne przesuwają się. Ten rodzaj deformacji może wystąpić tylko w ciałach stałych, które mają wystarczającą sztywność, aby sprzeciwić się deformacji.

Z drugiej strony płyny nie oferują tego rodzaju oporu, ale mogą doświadczyć deformacji objętościowych.

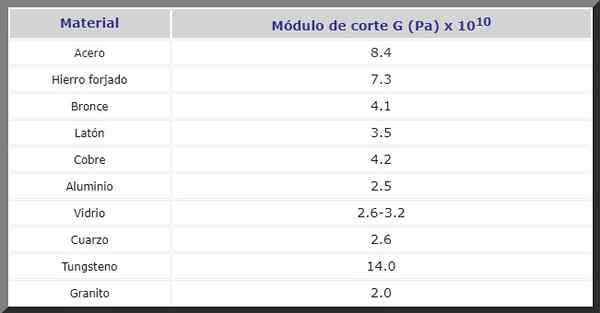
Rysunek 2. Śruby w strukturach podlegają wysiłkom cięcia. Źródło: Pixnio.

Następnie masz moduł G -Cut w P dla różnych materiałów często używanych w budowie oraz w produkcji maszyn i części zamiennych wszelkiego rodzaju:

Eksperymentalna miara modułu cięcia

Aby znaleźć wartość modułu cięcia, musisz przetestować próbki każdego materiału i zbadać odpowiedź na zastosowanie wysiłku tnącego.

Próbka to pręt wykonany z materiału z radiem R i długość L znany, który jest ustalony na jednym końcu, podczas gdy drugi łączy się z osą wolnego koła pasowego.

Koło pasowe ma wiązaną linę, na którego wolnym końcu zawieszone jest ważenie, które wywiera siłę F Na pręcie przez linę. A ta siła z kolei powoduje chwilę M W pręcie, który następnie obraca mały kąt θ.

Schemat montażu można zobaczyć na poniższym rysunku:

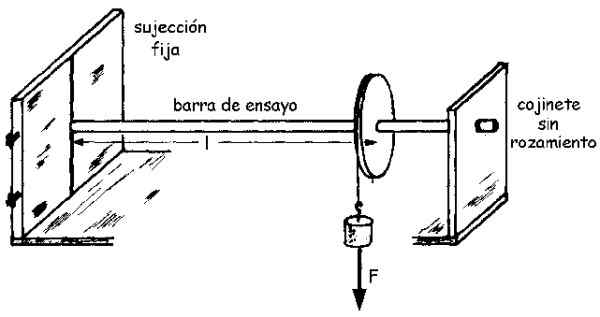Rysunek 3.- Zespół eksperymentalny w celu określenia modułu ścinania lub cięcia cienkiego paska testowego. Źródło: University of Valladolid.

Wielkość chwili M, które oznaczamy jako M (bez pogrubienia) jest związany z obróconym kątem θ przez moduł wycięty g zgodnie z następującym równaniem (jest wydedukowane przez prostą całkę):

Ponieważ wielkość momentu jest równa iloczynowi modułu siłowego według promienia koła pasowego r_P:

Może ci służyć: eksperyment Torricelli: miary ciśnienia atmosferycznego, znaczenie

M = f.R_P

A siła to ciężar, który wisi W, Więc:

M = w.R_P

Zastąpienie w równaniu wielkości momentu:

Masz związek między wagą a kątem:

Jak znaleźć g?

Ten związek między zmiennymi W I θ Jest liniowy, więc mierzone są różne kąt.

Pary o wadze i kąta są wykresami na papierze milimetrowym, najlepsza linia przechodząca przez punkty eksperymentalne jest dostosowywane i nachylenie jest obliczane M wspomnianej linii.

 Stamtąd następuje:

Ćwiczenia z rozwiązaniem

- Ćwiczenie 1

2 pręta.5 metrów długości i radio 4.5 mm jest ustalone na jednym końcu. Drugi łączy się z kołem pasowym 75 cm, który ma wagę 1 1.3 kg. Kąt obrócony wynosi 9.5.

Z tymi danymi wymaga się obliczenia modułu wyciętego G pręta.

Rozwiązanie

Z równania:

Gasses G:

A wartości podane w instrukcji zostały zastąpione, uważając, aby wyrazić wszystkie dane w międzynarodowym systemie jednostek, jeżeli:

R = 4.5 mm = 4.5 x 10 ^-3 M

R_P = 75 cm = 0.075

Przejść od kilogramów (są to w rzeczywistości kilogramy - siły) do Newton pomnoży przez 9.8:

W = 1.3 kg force = 1.3 x 9.8 n = 12.74 n

I wreszcie stopnie muszą być na Radianach:

9.5 = 9.5 x2π /360 radian = 0.1658 radian.

Z tym wszystkim masz:

= 2.237 x 10¹⁰ Rocznie

- Ćwiczenie 2

Kostka żelowa ma 30 cm. Jedna z jego twarzy jest ustalona, ​​ale jednocześnie siła równoległa 1 N jest przyłożona do przeciwnej twarzy, która dzięki temu porusza się 1 cm (patrz przykład książki na rycinie 1).

Może ci służyć: magnetyzacja: moment magnetyczny orbital i spin, przykłady

Poproszono o obliczenie za pomocą tych danych:

a) Wielkość naprężenia ścinającego

b) Jednolitowe deformacja δ

c) wartość modułu cięcia

Rozwiązanie

Wielkość naprężenia ścinającego wynosi:

τ = f/a

Z:

A = strona² = (30 x 10^-2 cm)² = 0.09 m²

Dlatego:

τ = 1 N / 0.09 m² = 11.1 Pa

Rozwiązanie b

Jednostki deformacji jest niczym innym jak wartością δ, podaną przez:

δ = δx / l

Przemieszczenie twarzy poddanej sile wynosi 1 cm, więc:

δ = 1/30 = 0.0333

Rozwiązanie c

Moduł tnąca i iloraz między wysiłkiem cięcia a deformacją jednostki:

G = wysiłek cięcia/deformacji

Dlatego:

G = 11.1 pa /0.033 = 336.4 Pa

Bibliografia

1. Piwo, f. 2010. Mechanika materiałów. McGraw Hill. 5. Wydanie.
2. Franco Garcia, do. Sztywne stałe. Usłyszeć pomiar modułu. Źródło: SC.Ehu.Jest.
3. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6th. Ed Prentice Hall.
4. Resnick, r. (1999). Fizyczny. Tom. 1. Wydanie trzecie. po hiszpańsku. Continental Editorial Company S.DO. c.V.
5. University of Valladolid. Department of Physics of Condensed Matter. Wybór problemów. Odzyskane z: www4.winogrono.Jest.