Przykłady nieruchomości, przykłady

Własność Algebra Lock Jest to zjawisko, które wiąże dwa elementy zestawu z operacją, w którym warunkiem niezbędnym jest to, że po 2 elementach w ramach wspomnianej operacji wynik należy również do zestawu początkowego.

Na przykład, jeśli liczby parzyste są traktowane jako całość i suma jako operacja, uzyskana jest zamek wspomnianego zestawu w odniesieniu do sumy. Wynika to z faktu, że suma 2 równych liczb będzie zawsze podawana w rezultacie inna liczba, w ten sposób spełniając warunek blokady.

Źródło: Unspash.com

[TOC]

Charakterystyka

Istnieje wiele właściwości, które determinują przestrzenie lub ciała algebraiczne, takie jak struktury lub pierścienie. Jednak nieruchomość Lock jest jedną z najbardziej znanych w ramach podstawowej algebry.

Nie wszystkie zastosowania tych właściwości są oparte na zjawiskach lub elementach numerycznych. Wiele codziennych przykładów może działać z algebraicznego podejścia do czystego.

Przykładem może być obywatele kraju, który przyjmuje wszelkiego rodzaju stosunki prawne, takie jak społeczeństwo handlowe lub małżeńskie. Po tej operacji lub zarządzaniu nadal są obywatelami kraju. Zatem operacje obywatelskie i zarządzania w odniesieniu do dwóch obywateli reprezentują zamek.

Algebra numeryczna

W odniesieniu do liczb istnieje wiele aspektów, które były powodem do nauki w różnych prądach matematyki i algebry. Z tych badań wyłoniła się duża liczba aksjomatów i twierdzeń, które służą jako teoretyczne podstawy współczesnych badań i prac.

Jeśli pracujesz z zestawami numerycznymi, możemy ustalić inną ważną definicję właściwości blokady. Mówi się, że jeden zestaw A jest zamkiem innego zestawu B, jeśli A jest najmniejszym zestawem, który zawiera wszystkie zestawy i operacje, które dom B.

Może ci służyć: nieruchomość dystrybucyjna

Demonstracja

Demonstracja blokady stosuje się do elementów i operacji obecnych w zbiorze rzeczywistych liczb n.

Niech a i b będą dwiema liczbami należącymi do zestawu r, blokada tych elementów jest zdefiniowana dla każdej operacji zawartej w r.

Dodatek

- SUM: ∀ A ˄ B ∈ R → A + B = C ∈ R

To jest algebraiczny sposób, aby to powiedzieć Dla wszystkich A i B, które należy do liczb rzeczywistych, musi to być suma A więcej B jest równa C, która również należy do rzeczywistości.

Łatwo jest sprawdzić, czy ta propozycja jest prawdziwa; Wystarczy, aby suma między dowolną liczbą rzeczywistą i sprawdzić, czy wynik należy również do liczb rzeczywistych.

3 + 2 = 5 ∈ R

-2 + (-7) = -9 ∈ R

-3 + 1/3 = -8/3 ∈ R

5/2 + (-2/3) = 11/6 ∈ R

Obserwuje się, że warunek blokady jest spełniony dla liczb rzeczywistych i suma. W ten sposób można to zakończyć: Suma liczb rzeczywistych to zamek algebraiczny.

Mnożenie

- Mnożenie: ∀ A ˄ B ∈ R → A . B = C ∈ R

Dla wszystkich A i B, które należy do prawdziwych, pomnożenie A dla B jest równe C, co również należy do rzeczywistości.

Podczas weryfikacji za pomocą tych samych elementów poprzedniego przykładu obserwowane są następujące wyniki.

3 x 2 = 6 ∈ R

-2 x (-7) = 14 ∈ R

-3 x 1/3 = -1 ∈ R

5/2 x (-2/3) = -5/3 ∈ R

Jest to wystarczający dowód, aby stwierdzić, że: Mnożenie liczb rzeczywistych to zamek algebraiczny.

Ta definicja można rozszerzyć na wszystkie operacje liczb rzeczywistych, chociaż znajdziemy określone wyjątki.

Źródło: Pixabay.com

Specjalne przypadki w R

Dział

Jako szczególny przypadek obserwuje się podział, w którym doceniany jest następujący wyjątek:

Może ci służyć: klasyczne prawdopodobieństwo: obliczenia, przykłady, rozwiązane ćwiczenia

∀ A ˄ B ∈ R → A / B ∉ R ↔ B = 0

Dla wszystkich A i B, które należą R Musi między b, nie należy do reais, jeśli i tylko wtedy, gdy b jest równe zero.

Ten przypadek odnosi się do ograniczenia niemożności podziału między zero. Ponieważ zero należy do liczb rzeczywistych, stwierdza się, że: LPodział nie jest zamkiem w rzeczywistości.

Radio

Istnieją również operacje potencjałów, a dokładniej zgłoszenia, w których wyjątki są prezentowane dla radykalnych mocy wskaźnika momentu obrotowego:

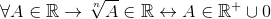; Z n par

Za wszystko, do czego należy do królewskiego.

W ten sposób oznacza, że ​​nawet korzenie mają zastosowanie tylko do pozytywnych rzeczywistych i stwierdza się, że wzmocnienie nie jest zamkiem w R.

Logarytm

Jest zatwierdzony do funkcji logarytmicznej, która nie jest zdefiniowana dla wartości mniejszych lub równych zero. Aby sprawdzić, czy logarytm jest blokadą R przebiega w następujący sposób:

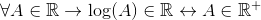
W przypadku wszystkiego, do czego należy do reais, logarytm A należy do reais, jeśli i tylko wtedy, gdy należy do pozytywnego rzeczywistości.

Gdy wartości negatywne i zerowe, które również należą do R, można potwierdzić, że:

Logarytm nie jest zamkiem liczb rzeczywistych.

Przykłady

Sprawdź blokadę pod kątem sumy i odejmowania liczb naturalnych:

Suma w n

Pierwszą rzeczą jest sprawdzenie warunku blokady dla różnych elementów danego zestawu, gdzie zaobserwowano, że niektóre elementy pękają z warunkiem, istnienie blokady można automatycznie odmówić.

Może ci służyć: Radio zbieżności: definicja, przykłady i ćwiczenia rozwiązane

Ta właściwość jest spełniona dla wszystkich możliwych wartości A i B, jak zaobserwowano w następujących operacjach:

1 + 3 = 4 ∈ N

5 + 7 = 12 ∈ N

1000 + 10000 = 11000 ∈ N

Nie ma żadnych naturalnych wartości, które przełamują warunek blokady, więc kończy się:

Suma jest zamkiem w n.

Odejmuje w n

Poszukiwane są naturalne elementy zdolne do złamania stanu; A - b należy do tubylców.

Działanie jest łatwo znaleźć pary naturalnych elementów, które nie spełniają warunków blokady. Na przykład:

7 - 10 = -3 ∉ a n

W ten sposób możemy stwierdzić, że:

Odejmowanie nie jest zamkiem zestawu liczb naturalnych.

Proponowane ćwiczenia

1-SAMP.

2-Wykres, jeśli zbiór liczb rzeczywistych jest zamkiem całej całej liczby.

3-określony, który zestaw liczbowy może być zamkiem liczb rzeczywistych.

4-próbka właściwość blokady dla zestawu liczb wyimaginowanych, w odniesieniu do sumy, odejmowania, mnożenia i podziału.

Bibliografia

1. Panorama of Pure Mathematics: The Bourbakist Choice. Jean Dieudonné. Reverte, 1987.
2. Teoria liczb algebraicznych. Alejandro J. Díaz Barriga, Ana Irene Ramírez, Francisco Tomás. National Autonomous University of Mexico, 1975.
3. Algebra liniowa i jej aplikacje. Sandra Ibeth Ochoa García, Eduardo Gutiérrez González.
4. Struktury algebraiczne V: Teoria ciała. Héctor a. Merklen. Organizacja stanów amerykańskich, sekretariat generalny, 1979.
5. Wprowadzenie do algebry przemiennej. Michael Francis Atiyah, ja. G. MacDonald. Reverte, 1973.