Sum właściwości asocjacyjne, mnożenie, przykłady, ćwiczenia

łączność sumy reprezentuje asocjacyjny charakter operacji dodaje się do różnych zestawów matematycznych. Opowiada trzy (lub więcej) elementów tych zestawów, zwanych A, B i C, tak że zawsze się spełniło:

A + (B + C) = (A + B) + C

W ten sposób gwarantuje się, że niezależnie od tego, jak grupować operację, wynik jest taki sam.

Rysunek 1. Wiele razy używamy właściwości asocjacyjnej sum. (Rysunek: kompozycja Freepik: F. Zapata)

Należy jednak zauważyć, że właściwość asocjacyjna nie jest synonimem własności przemiennej. To znaczy wiemy, że kolejność dodatków nie zmienia sumy lub że kolejność czynników nie zmienia produktu. Więc dla suma możesz napisać w ten sposób: a + b = b + a.

Jednak we właściwościach asocjacyjnych jest inaczej, ponieważ kolejność dodawania elementów jest utrzymywana i jakie zmiany to operacja, która jest wykonywana jako pierwsza. Co oznacza, że ​​nie ma znaczenia jako pierwszego (B+C) i do tego wyniku dodaj, aby zacząć dodawać do B i do wyniku Dodaj C.

Wiele ważnych operacji, takich jak suma, jest asocjacyjnymi, ale nie wszystkie. Na przykład w odjęciu liczb rzeczywistych zdarza się, że:

A - (b - c) ≠ (a - b) - c

Tak a = 2, b = 3, c = 1, następnie:

2- (3 - 1) ≠ (2 - 3) - 1

0 ≠ -2

[TOC]

Właściwość asocjacyjna mnożenia

Jak to miało miejsce dla suma, właściwość asocjacyjna mnożenia wskazuje, że:

a ˟ (b ˟ c) = (a ˟ b) ˟ c

Może ci służyć: suma wielomianów, jak to się dzieje, przykłady, ćwiczenia

W przypadku zestawu liczb rzeczywistych łatwo jest sprawdzić, czy zawsze jest. Na przykład używając wartości a = 2, b = 3, c = 1, musisz:

2 _˟ (3 _˟ 1) = (2 _˟  3) _˟ 1 → 2 _˟ 3 = 6 _˟ 1

6 = 6

Liczby rzeczywiste spełniają właściwość asocjacyjną zarówno sumy, jak i mnożenia. Z drugiej strony, w innym zestawie, podobnie jak wektory, suma jest asocjacyjna, ale produkt krzyżowy lub produkt wektorowy nie jest.

Zastosowania właściwości asocjacyjnej mnożenia

Zaletą, że operacje, w których spełnia się właściwość asocjacyjna, jest grupowanie w najwygodniejszy sposób. To bardzo ułatwia rozdzielczość.

Załóżmy na przykład, że w małej bibliotece znajdują się 3 półki z 5 rozrywkami. W każdej rozrywce jest 8 książek. Ile książek jest w sumie?

Możemy wykonać tę operację w następujący sposób: Total Books = (3 x 5) x 8 = 15 x 8 = 120 książek.

Lub tak: 3 x (5 x 8) = 3 x 40 = 120 książek.

Rysunek 2. Zastosowaniem właściwości asocjacyjnej mnożenia jest obliczenie liczby książek na każdej półce. Obraz utworzony przez f. Zapata.

Przykłady

-W zestawach liczb naturalnych, całości, racjonalnych, nieruchomości i złożonych właściwość suma i mnożenia jest spełniona.

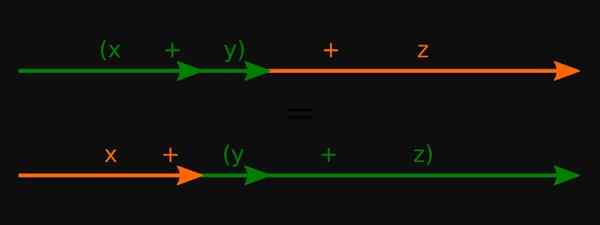Rysunek 3. W przypadku liczb rzeczywistych własność sum. Źródło: Wikimedia Commons.

-W przypadku wielomianów stosuje się również w tych operacjach.

-W przypadkach operacji odejmowania, podziału i wykładników właściwość asocjacyjna nie jest wypełniona w liczbach rzeczywistych ani wielomianowych.

Może ci służyć: ortoedro: wzory, obszar, objętość, przekątna, przykłady

-W przypadku macierzy właściwość asocjacyjna jest spełniona dla sumy i mnożenia, chociaż w tym drugim przypadku powściągliwość nie jest spełniona. Oznacza to, że biorąc pod uwagę matryce A, B i C, prawdą jest:

(A x b) x c = a x (b x c)

Ale ... a x b ≠ b x a

Własność asocjacyjna w wektorach

Wektory tworzą inny zestaw niż liczby rzeczywiste lub liczby złożone. Operacje zdefiniowane dla zestawu wektorów są nieco inne: istnieje suma, odejmowanie i trzy typy produktów.

Suma wektorów spełnia właściwość asocjacyjną, a także liczby, wielomiany i macierze. Jeśli chodzi o produkty skalarne, wspinanie się według wektora i krzyża, które są wytwarzane między wektorami, ten ostatni nie spotyka się, ale produkt skalarny, który jest innym rodzajem operacji między wektorami, spełnia go, biorąc pod uwagę następujące:

-Produkt skalarny dla wektora powoduje wektor.

-A wspinając się po dwóch wektorach, jest to skalar.

Dlatego biorąc pod uwagę wektory v, Lub I W, A ponadto skalar λ można napisać:

-Suma wektorów: v +(Lub + W ) = (v + Lub) + W

-Produkt skalarny: λ (v • • Lub ) = (λv) • Lub

Ten ostatni jest możliwy dzięki temu v • • Lub Jest to skalar i λv To wektor.

Jednakże:

v × (Lub × W ) ≠ (v × Lub)×W

Faktoralizacja wielomianowa poprzez grupowanie warunków

Ta aplikacja jest bardzo interesująca, ponieważ jak wspomniano powyżej, właściwość asocjacyjna pomaga rozwiązać pewne problemy. Suma monomianów jest asocjacyjna i można to zastosować do uwzględnienia, gdy oczywisty wspólny czynnik nie pojawia się na pierwszy rzut oka.

Może ci służyć: wypukły wielokąta: definicja, elementy, właściwości, przykłady

Załóżmy na przykład, że należy go uwzględnić: X³ + 2X² + 3X +6. Ten wielomian nie ma wspólnego czynnika, ale zobaczmy, co się stanie, jeśli jest zgrupowany w ten sposób:

X³ + 2x² + 3x +6 = (x³ + 2x²) + (3x +6)

Pierwszy nawias ma jako wspólny czynnik X²:

X³ + 2X² = X² (x+2)

W drugim współczynniku to 3:

3x +6 = 3 (x + 2)

Więc:

X³ + 2X² + 3X +6 = X²(x+ 2)+ 3 (x+ 2)

Teraz istnieje oczywisty wspólny czynnik, który jest x+2:

X²(x+ 2)+ 3 (x+ 2) = (x+ 2) (x²+3)

Ćwiczenia

- Ćwiczenie 1

Budowanie szkoły ma 4 piętra, aw każdej z nich znajduje się 12 klas z 30 biurkami w środku. Ile biur ma w sumie szkołę?

Rozwiązanie

Ten problem jest rozwiązany poprzez zastosowanie właściwości asocjacyjnej mnożenia, zobaczmy:

Całkowita liczba biur = 4 piętra x 12 klas /podłoga x 30 biurka /klasa = (4 x 12) x 30 biur = 48 x 30 = 1440 biurka.

O Jeśli preferowane: 4 x (12 x 30) = 4 x 360 = 1440 biur

- Ćwiczenie 2

Biorąc pod uwagę wielomiany:

A (x) = 5x³ + 2x² -7x + 1

B (x) = x⁴ +6x³ -5x

C (x) = -8x² +3x -7

Zastosuj właściwość asocjacyjną sumy, aby znaleźć (x) + b (x) + c (x).

Rozwiązanie

Pierwsze dwa można pogrupować, a wynik dodaje trzeci:

A (x) + b (x) = [5x³ + 2x² -7x + 1] + [x⁴ +6x³ -5x] = x⁴ + 11x³+ 2x² -12x +1

Natychmiast dodaje się wielomianowy C (x):

[X⁴ + 11x³+ 2x² -12x +1] + [-8x² +3x -7] = x⁴ + 11x³ - 6x² -9x -6

Czytnik może sprawdzić, czy wynik jest identyczny, jeśli zostanie rozwiązany według opcji A (x) + [b (x) + c (x)]]].

Bibliografia

1. Jiménez, r. 2008. Algebra. Prentice Hall.
2. Matematyka jest zabawna. Prawa przemienne, asocjacyjne i okręgowe. Odzyskany z: Mathisfun.com.
3. Math Mashhouse. Definicja właściwości asocjacyjnej. Odzyskane z: Mathwarehouse.com.
4. Naukowe. Właściwość asocjacyjna i przemienna dodawania i mnożenia (z przykładem). Odzyskane z: naukowe.com.
5. Wikipedia. Łączność. Źródło: w:.Wikipedia.org.