Niezwykłe produkty

Jakie są znaczące produkty?

Godne uwagi produkty to operacje algebraiczne, w których wyrażane są mnożenie wielomianów, których nie trzeba tradycyjnie rozwiązywać, ale za pomocą niektórych reguł można znaleźć wyniki tego samego.

Wielomiany są mnożone przez to, czy, dlatego możliwe jest, że mają wiele terminów i zmiennych. Aby ten proces był krótki, stosowane są zasady godnych uwagi produktów, które umożliwiają mnożenie bez konieczności terminu.

Godne uwagi produkty i przykłady

Każdy niezwykły produkt jest formułem wynikającym z czynników uwzględnienia, złożonego z wielomianów kilku terminów, takich jak dwumianowe lub trynomiaki, zwane czynnikami.

Czynniki są podstawą mocy i mają wykładnik. Gdy czynniki się mnożą, należy dodać wykładniki.

Istnieje kilka godnych uwagi wzorów produktów, niektóre są bardziej używane niż inne, w zależności od wielomianów i są następujące:

Kwadratowy dwumian

Jest to mnożenie dwumianatu samego, wyrażonego w postaci mocy, gdzie terminy są dodawane lub odejmowane:

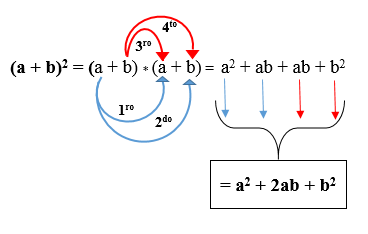
Do. Kwadratowa suma dwumianowa: Jest równy kwadratu pierwszego terminu, a także podwójnie iloczyn terminów, a także kwadrat drugiego terminu. Wyraża się to w następujący sposób:

(A + B)² = (A + B) _* (A + B).

Na poniższym rysunku możesz zobaczyć, w jaki sposób produkt jest opracowywany zgodnie z wyżej wymienioną zasadą. Wynik nazywa się trynomikiem idealnego kwadratu.

Przykład 1

(x + 5) ² = x² + 2 (x * 5) + 5²

(x + 5) ² = x² + 2 (5x) + 25

(x + 5) ² = x² + 10x + 25.

Przykład 2

(4a + 2b) = (4a)² + 2 (4 _* 2b) + (2b)²

(4a + 2b) = 8a² + 2 (8ab) + 4b²

(4a + 2b) = 8a² + 16 AB + 4B².

B. Dwumianowa kwadratowego odejmowania: Zastosowana jest ta sama zasada dwumianowa sumy, tylko że w tym przypadku drugi termin jest ujemny. Jego formuła jest następująca:

(A - B)² = [(a) + (- b)]²

Może ci służyć: analogie numeryczne: typy, aplikacje i ćwiczenia

(A - B)² = a² +2 _* (-B) + (-B)²

(A - B)²   = a² - 2AB + b².

Przykład 1

(2x - 6)² = (2x)² - 2 (2x _* 6) + 6²

(2x - 6)²  = 4x² - 2 (12x) + 36

(2x - 6)² = 4x² - 24x + 36.

Produkt koniugatu bunionerów

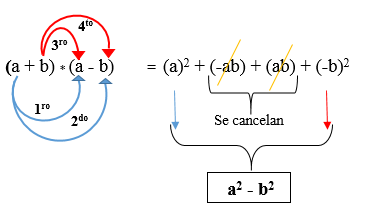
Dwa dwumianowe są sprzężone, gdy drugie warunki każdego z nich mają różne znaki, to znaczy pierwszego jest pozytywna i drugiej negatywnej lub odwrotnie. Jest to rozwiązywane przez podniesienie każdego monomicznego kwadratu i odejmowane. Jego formuła jest następująca:

(A + B) _* (A - B)

Na poniższym rysunku opracowano iloczyn dwóch sprzężonych dwumianów, w którym obserwuje się, że wynik jest różnicą kwadratów.

Przykład 1

(2a + 3b) (2a - 3b) = 4a² + (-6AB) + (6 AB) + (-9b²)

(2a + 3b) (2a - 3b) = 4a² - 9b².

Produkt dwóch dwumianów z powszechnym terminem

Jest to jeden z najbardziej złożonych i mało używanych produktów, ponieważ jest to mnożenie dwóch dwumianów, które mają wspólny termin. Reguła wskazuje następujące:

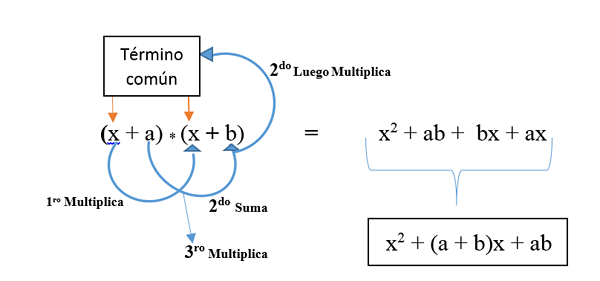
• Kwadrat wspólnego terminu.
• Plus suma terminy, które nie są powszechne, a następnie pomnóż je przez wspólny termin.
• Plus suma pomnożenia terminów, które nie są powszechne.

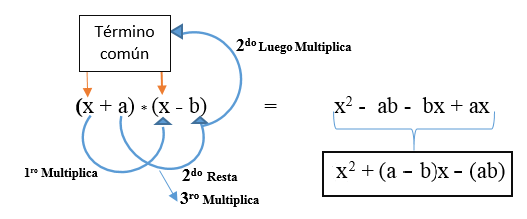
Jest reprezentowany w wzorze: (x + a) _* (x + b) i jest opracowywany, jak pokazano na obrazie. Rezultatem jest nieskrępowany kwadratowy trynomial.

Przykład 1

(x + 6) _* (x + 9) = x² + (6 + 9) _* X + (6 _* 9)

(x + 6) _* (x + 9) = x² + 15x + 54.

Istnieje możliwość, że drugi termin (inny termin) jest ujemny, a jego wzór jest następujący: (x + a) _* (x - b).

Przykład 2

(7x + 4) _* (7x - 2) = (7x _* 7x) + (4 - 2)_* 7x + (4 _* -2)

(7x + 4) _* (7x - 2) = 49x² + (2)_* 7x - 8

(7x + 4) _* (7x - 2) = 49x² + 14x - 8.

Może się zdarzyć, że oba różne terminy są negatywne. Twoja formuła będzie: (x - a) _* (x - b).

Może ci służyć: twierdzenie Lamy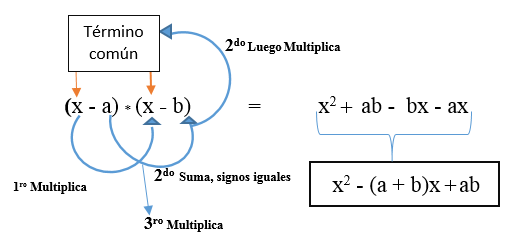

Przykład 3

(3b - 6) _* (3b - 5) = (3b _* 3b) + (-6 - 5)_* (3b) + (-6 _* -5)

(3b - 6) _* (3b - 5) = 9b² + (-jedenaście) _* (3b) + (30)

(3b - 6) _* (3b - 5) = 9b² - 33b + 30.

Kwadratowy wielomian

W takim przypadku istnieją więcej niż dwa terminy i aby je rozwinąć, każdy z nich jest cięty i wciągany razem z mnożeniem jednego terminu za pomocą drugiego; Jego formuła to: (A + B + C)² A wynikiem operacji jest trójmianowy kwadrat.

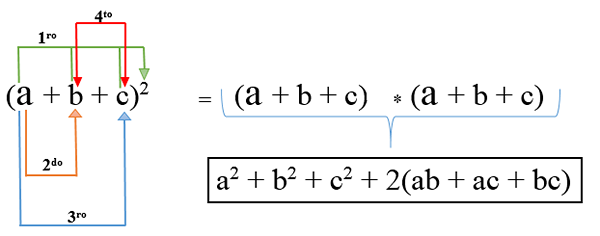
Przykład 1

(3x + 2y + 4z)² = (3x)² + (2 i)² + (4z)² + 2 (6xy + 12xz + 8yz)

(3x + 2y + 4z)² = 9x² + 4y² + 16Z² + 12xy + 24xz + 16yz.

Kostka dwumianowa

Jest to złożony produkt. Aby go rozwinąć, dwumianowa jest mnożona przez jego kwadrat, w następujący sposób:

Do. Dla dwumianowego do kostki suma:

• Kostka pierwszego terminu oraz potrójna kwadrat pierwszego okresu według drugiego.
• Plus Triple w pierwszym okresie, według drugiego kwadratu.
• Plus kostka drugiego terminu.

(A + B)³ = (A + B) _* (A + B)²

(A + B)³ = (A + B) _* (Do² + 2AB + b²)

(A + B)³ = a³ + 2²B + AB² + BA² + 2AB² + B³

(A + B)³ = a³ + 3²B + 3AB² + B³.

Przykład 1

(A + 3)³ = a³ + 3 (a)²_*(3) + 3 (a)_*(3)² + (3)³

(A + 3)³ = a³ + 3 (a)²_*(3) + 3 (a)_*(9) + 27

(A + 3)³ = a³ + 9 a² + 27a + 27.

B. Dla dwumianowego do sześcianu odejmowania:

• Sześcian pierwszego terminu, z wyjątkiem potrójnego kwadratu pierwszego okresu według drugiego.
• Plus Triple w pierwszym okresie, według drugiego kwadratu.
• Mniej sześcian drugiego terminu.

(A - B)³ = (a - b) _* (A - B)²

(A - B)³ = (a - b) _* (Do² - 2AB + b²)

(A - B)³ = a³ - 2²B + AB² - BA² + 2AB² - B³

(A - B)³ = Do³ - 3²B + 3AB² - B³.

Przykład 2

(B - 5)³ = b³ + 3 (b)²_*(-5) + 3 (b)_*(-5)² + (-5)³

(B - 5)³ = b³ + 3 (b)²_*(-5) + 3 (b)_*(25) -125

Może ci służyć: Dane bez grupy: Przykłady i ćwiczenia rozwiązane

(B - 5)³ = b³ - 15b² +75b - 125.

Trinomialna kostka

Rozwija go przez kwadrat. Jest to bardzo obszerny niezwykły produkt, ponieważ na sześcianie są podniesione 3 terminy, a także potrójnie każdego terminu kwadratowego, pomnożone przez każdy z terminów. Widoczne w lepszej formie:

(A + B + C)³ = (A + B + C) _* (A + B + C)²

(A + B + C)³ = (A + B + C) _* (Do² + B² + C² + 2AB + 2AC + 2BC)

(A + B + C)³ = A³ + B³ + C³ + 3²B + 3AB² + 3²C + 3AC² + 3b²C + 3BC² + 6ABC.

Przykład 1

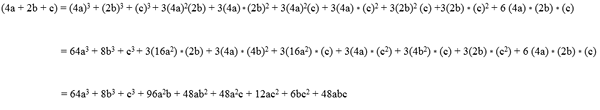
Rozwiązywane ćwiczenia godnych uwagi produktów

Ćwiczenie 1

Rozwiń następujący dwumian do kostki: (4x - 6)³.

Rozwiązanie

Pamiętając, że dwumianowa kostki jest równa pierwszego terminu podniesionego do sześcianu, z wyjątkiem potrójnego kwadratu pierwszego okresu do drugiego; Plus potrójnie pierwszy termin, według drugiego kwadratu, z wyjątkiem sześcianu drugiego terminu.

(4x - 6)³ = (4x)³ - 3 (4x)²(6) + 3 (4x) _* (6)² - (6)²

(4x - 6)³ = 64x³ - 3 (16x²) (6) + 3 (4x)_* (36) - 36

(4x - 6)³ = 64x³ - 288x² + 432x - 36.

Ćwiczenie 2

Opracuj następujący dwumian: (x + 3) (x + 8).

Rozwiązanie

Masz dwumianowy, w którym jest wspólny termin, a drugi termin jest dodatni. Aby go rozwinąć, należy zwiększyć tylko wspólny termin, a także suma terminów, które nie są powszechne (3 i 8), a następnie pomnożyć je przez wspólny termin.

(x + 3) (x + 8) = x² + (3 + 8) x + (3_*8)

(x + 3) (x + 8) = x² + 11x + 24.

Bibliografia

1. Anioł, a. R. (2007). Algebra podstawowa. Edukacja Pearsona,.
2. Arthur Goodman, L. H. ( 1996). Algebra i trygonometria z geometrią analityczną. Edukacja Pearsona.
3. Das, s. (S.F.). Maths Plus 8. Wielka Brytania: Sagar Ratna.
4. Jerome e. Kaufmann, k. L. (2011). Algebra elementarna i pośrednia: połączone podejście. Floryda: Cengage Learning.
5. Pérez, c. D. (2010). Edukacja Pearsona.