Adiabatyczne typy procesów, przykłady, ćwiczenia rozwiązane

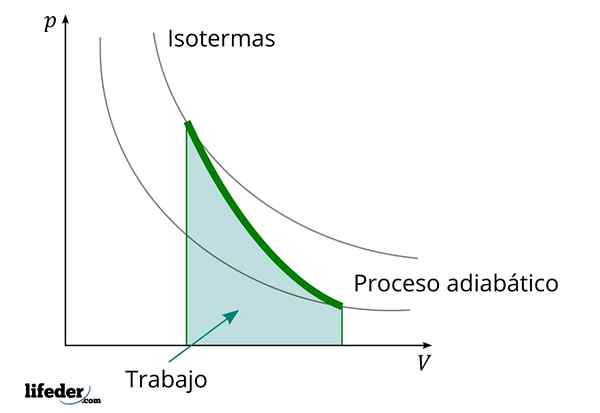
A Proces adiabatyczny Jest to ten, w którym nie ma wymiany ciepła między systemem a jego otoczeniem, albo dlatego, że występuje on w medium izolacyjnym, albo dlatego, że mija bardzo szybko. Oznacza to, że w otoczeniu systemu jest to część badanego wszechświata, zmiany temperatury nie powinny być postrzegane, ale tylko działać.

Jest to jeden z podstawowych procesów termodynamiki. W przeciwieństwie do innych procesów (izokorycznych, izobarycznych i izotermicznych), żadna z jego zmiennych fizycznych nie pozostaje stała; to znaczy wielkości ciśnienia, objętości, temperatury i entropii zmieniają się w miarę ewolucji procesu adiabatycznego.

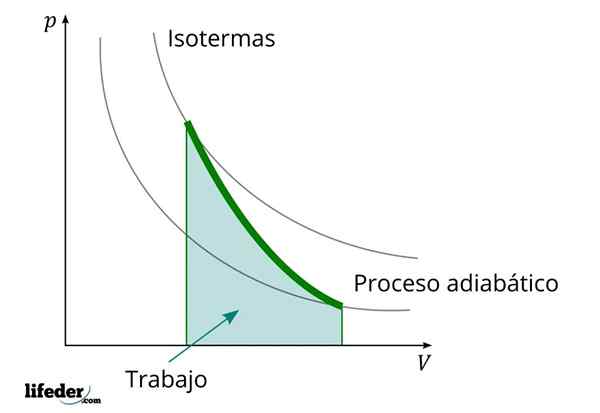Podczas procesu adiabatycznego, w którym zwiększa się objętość, wewnętrzna energia substancji, którą praca zmniejsza

Inną ważną cechą procesów adiabatycznych jest to, że przeprowadzają one lub spożywają pracę proporcjonalnie do zmienności energii wewnętrznej ich systemów; W tym przypadku cząsteczek jego cząsteczek w fazie gazowej. Można to wykazać dzięki pierwszemu prawowi termodynamiki.

W życiu codziennym ten rodzaj procesu obejmuje przede wszystkim zjawiska geofizyczne i, do pewnego stopnia, funkcjonowanie tłoków w silnikach Diesla. Transfer ciepła często zapobiega użyciu medium izolacyjnego, ale to szybkość tych procesów pozwala na ich prawdziwy rozwój.

[TOC]

Odwracalne i nieodwracalne procesy adiabatyczne

Odwracalny

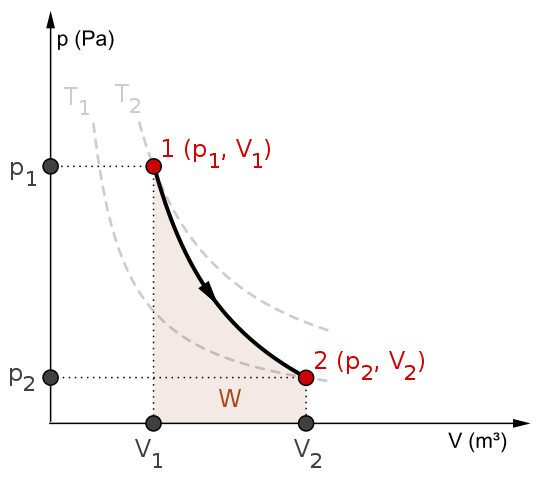Schemat P-V i praca w procesie adiabatycznym. Źródło: Mikerun/CC BY-SA (https: // creativeCommons.Org/licencje/nabrzeże/4.0)

Procesy adiabatyczne mogą być odwracalne lub nieodwracalne. Jednak te pierwsze istnieją tylko jako teoretyczne narzędzia do badania tego drugiego. Zatem odwracalne procesy adiabatyczne obejmują idealne gazy i brak tarcie i innej ewentualności, które powodują przenoszenie ciepła między systemem a jego otoczeniem.

Rozważmy na przykład schemat P-V dla odwracalnego procesu adiabatycznego z góry. T₁ oraz T₂ odpowiadają dwóm izotermom, na których presja P i tomy V systemu różnią się.

Wśród stanów (str₁, V₁) I p₂, V₂) Wykonuje się odwracalne rozszerzenie adiabatyczne, ponieważ przechodzimy od tomu V₁ do jednego v₂, większy, po kierunku strzałki.

W ten sposób system chłodzi, ale bez przestrzegania zachowania izoterm. Obszar pod krzywą odpowiada pracy W, której wartość jest dodatnia, ponieważ jest to rozszerzenie.

W tym procesie entropia pozostaje stała i dlatego mówi się, że jest izontropika. Matematyczne przetwarzanie tej odwracalności generuje zestaw równań, z którymi można ocenić inne systemy.

Może ci służyć: komórki elektrolityczne

Nieodwracalny

Nieodwracalne procesy adiabatyczne, w przeciwieństwie do tych odwracalnych, nie są graficzne na schematach p-v z ciągłymi, ale kropkowanymi liniami, ponieważ tylko stany końcowe i początkowe mają swoje zmienne (p, v i t) dobrze zdefiniowane. Procesy te obejmują rzeczywiste gazy, więc równanie gazów idealnych i ich pochodnych nie ma bezpośrednio zastosowania do nich.

Przechodzą szybko, zapobiegając przenoszeniu ciepła między systemem a jego otoczeniem. Również w nich entropia wzrasta, jak stwierdzono w drugim prawie termodynamiki.

Przykłady procesów adiabatycznych

Pojemność izolacyjna, taka jak ta prezentowana przez termos, jest jednym z kluczowych czynników procesu rozwijania adiabatycznego

Niektóre przykłady procesów adiabatycznych zostaną wymienione poniżej.

Ekspansja i zrozumienie

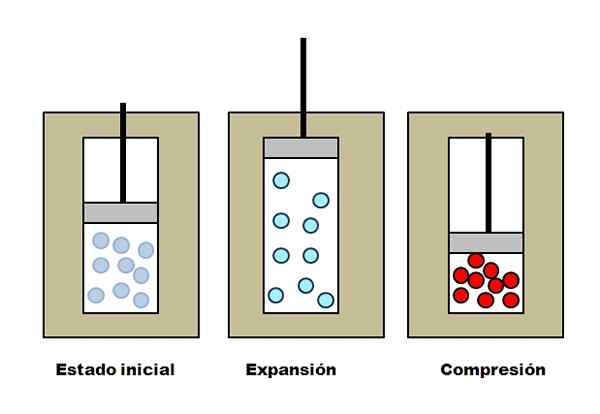Rozszerzenie i zrozumienie adiabatyczne. Źródło: Gabriel Bolívar.

Załóżmy, że trzy kamizelki izolacyjne zawierające przedziały pełne gazem. W stanie początkowym tłok nie ma nacisku na gaz. Następnie tłok może wzrastać, co zwiększa objętość, w której mogą się poruszać cząsteczki gazowe, powodując spadek energii wewnętrznej; A zatem spadek temperatury.

Wręcz przeciwnie do kompresji adiabatycznej: tłok wykonuje prace nad gazem, zmniejszając objętość, którą mogą zajmować jego cząsteczki. Tym razem energia wewnętrzna wzrasta, co sugeruje również wzrost temperatury, którego ciepło nie może rozproszyć się w kierunku otoczenia z powodu kamizelki izolacyjnej.

Magma Ascent

Kanały, w których magma unosi się wewnątrz wulkanu, mówią jako pożywka izolacyjna, która zapobiega przenoszeniu ciepła między magmą a atmosferą.

Rozprzestrzenianie się dźwięku

Gazy są zakłócane i rozszerzone zgodnie z falą dźwiękową bez chłodzenia lub gorącego powietrza, które je otaczają.

Efekt Foehna

Efekt Foehna jest przykładem procesów adiabatycznych w dziedzinie geofizyki. Masy powietrza wznoszą się w kierunku górnej części góry, w której odczuwają mniejszą presję, więc ich cząsteczki rozszerzają się i chłodzą, powodując powstanie chmury.

Jednak ledwo opadają po drugiej stronie góry, ciśnienie wzrasta, a zatem cząsteczki są ściśnięte i podnoszą temperaturę, powodując zniknięcie chmury.

Może ci służyć: chlorobenzen (C6H5CL)

W poniższym filmie zjawisko to można docenić:

Rozwiązane ćwiczenia

Wreszcie, kilka ćwiczeń zostanie rozwiązanych. Ważne jest, aby mieć pod ręką następujące równania:

Δu = Q - w (pierwsze prawo termodynamiki)

Ale brak transferu ciepła, q = 0 y:

Δu = - w (1)

To jest: jeśli praca W jest pozytywna, δu jest ujemna i odwrotnie. Z drugiej strony mamy również:

W = -NC_VΔT (2)

Że po zastosowaniu idealnego równania GASE (PV = NRT) oraz zastępowanie i rozwiązywanie dla t₂ oraz T₁ będziemy mieli:

W = (c_V/R) (p₁V₁ - P₂V₂) (3)

Będąc wartością R równą 0.082 L · atm/mol · k lub 8.314 J/mol · k

W procesach adiabatycznych ważne jest znanie związku C_P/C_V znany jako γ:

γ = c_P/C_V    (4)

Który umożliwia ustanowienie relacji T-V i P-V:

T₁V₁^γ-1 = T₂V₂^γ-1   (5)

P₁V₁^γ = P₂V₂^γ    (6)

A także przybliżone ciepły C_P i C_V Różnią się w zależności od tego, czy gazy są monoatomiczne, dwuatomiczne itp.

Ćwiczenie 1

Gaz wykonuje 600 J pracy za pomocą izolowanego przedziału. Jaka jest zmiana energii wewnętrznej? Czy temperatura zmniejsza lub rośnie? I biorąc pod uwagę, że jest to gaz monoatomiczny, również oblicz γ.

Dane:

W = +600J

Δu = ¿?

γ =?

W pracach jest pozytywna, ponieważ gaz pracuje nad otoczeniem. Będąc w izolowanym przedziale, q = 0, a zatem będziemy mieli równanie (1):

Δu = - w

To znaczy δu jest równe:

Δu = - (+600J)

= -600J

Co oznacza, że ​​wewnętrzna energia gazu zmniejszyła się o 600 j. Jeśli δu maleje, podobnie jest temperatura, więc gaz chłodzi się w wyniku wykonania pracy.

Ponieważ ten gaz jest monoatomiczny,

C_V = 3/2 r

C_P = 5/2 r

I bycie

γ = c_P/C_V

= (5/2 r)/(3/2 r)

= 5/3 lub 1.66

Ćwiczenie 2

W pojemniku 7 moli O₂ Zostały skompresowane z objętości 15 litrów do 9 litrów. Wiedząc, że początkowa temperatura wynosiła 300 K, oblicz: praca wykonana na gazie.

Dane:

N = 7 moli lub₂

T₁ = 300 K

V₁ = 15 l

V₂ = 9 l

W = ¿?

To nieodwracalne rozumienie adiabatyczne. Mamy dwa równania do rozwiązania W:

W = -NC_VΔT (2)

W = (c_V/R) (p₁V₁ - P₂V₂) (3)

Naciski mogą je obliczyć, ale aby zaoszczędzić czas, lepiej kontynuować z pierwszym z równań:

Może ci służyć: woda destylowana

W = -NC_VΔt

= -NC_V (T₂-T₁)

Potrzebujemy c_V oraz T₂ Aby określić w. Tlen, będący gazem dwuatomicznym, ma c_V równe 5/2 R:

C_V (ALBO₂) = 5/2 r

= 5/2 (8.314 J/mol · k)

= 20.785 J/mol · k

Musimy obliczyć t₂. Zwracamy się do równania (5):

T₁V₁^γ-1 = T₂V₂^γ-1

Ale zanim go użył, musisz określić najpierw C_P i γ:

C_P (ALBO₂) = 7/2 r

= 7/2 (8.314 J/mol · k)

= 29.099 J/mol · k

Bycie γ równym:

γ = c_P/C_V

= (29.099 J / mol · k) / 20.785 J/mol · k

= 1.4

Więc możemy to oczyścić₂ Z równania (5):

T₁V₁^γ-1 = T₂V₂^γ-1

T₂ = (T₁V₁^γ-1) / (V₂^γ-1)

= [(300k) (15l)^1.4-1] / (9L)^1.4-1

= 368.01 k

I wreszcie rozwiązujemy dla W:

W = -NC_VΔt

= -(7 mol o₂)( 20.785 J/mol · k) (368.01 K - 300 K)

= -9895.11 J O -9.895 kJ

Ćwiczenie 3

Neon pojemnik rozszerza się adiabatyczny i początkowo w temperaturze pokojowej (t = 298 tys.) Od 12 l do 14 l. Wiedząc, że jego początkowe ciśnienie wynosiło 3 atm, jaka będzie praca wykonana przez gaz?

Dane:

T₁ = 298 K

V₁ = 12 l

V₂ = 14 l

P₁ = 3 atm

W = ¿?

Równanie (3) pozwala nam określić w wartości ciśnień:

W = (c_V/R) (p₁V₁ - P₂V₂)

Ale brakuje nam C_V I p₂.

Końcowe ciśnienie można obliczyć za pomocą równania (6):

P₁V₁^γ = P₂V₂^γ

Bycie γ równym C_P/C_V. Ponieważ neon jest gazem monoatomicznym, mamy jego wartości C_P i C_V Mają odpowiednio 5/2R i 3/2R. Obliczamy wtedy γ:

γ = c_P/C_V

= (5/2R)/(3/2r)

= 5/3 lub 1.66

Oczyszczamy p₂ Z równania (6):

P₂ = (Str₁V₁^γ) / V₂^γ

= [(3 atm) (12 l)^5/3] / (14 l)^5/3

= 1.40 atm

A praca będzie równa:

W = (c_V/R) (p₁V₁ - P₂V₂)

= (3/2) [(3 atm) (12 l) - (1.40 atm) (14 l)] (101300 PA/1 ATM) (0.001 m³/L) (KJ/1000 J)

= 2.49 kJ

Współczynniki konwersji stosuje się do konwersji l · atm A Pa · m³, co odpowiada 1 J. Neon gaz rozszerza się, więc jego ciśnienie zmniejsza się, a podczas pracy nad otoczeniem jest to pozytywne. Ponadto jego energia wewnętrzna δu zmniejsza się, a także temperatura, chłodzenie w procesie ekspansji.

Bibliografia

1. Walter J. Moore. (1963). Chemia fizyczna. W kinetyce chemicznej. Czwarta edycja, Longmans.
2. Iran. Levine. (2009). Zasady fizykochemii. Szósta edycja. MC Graw Hill.
3. Wikipedia. (2020). Proces adiabatyczny. Źródło: w:.Wikipedia.org
4. Jones, Andrew Zimmerman. (18 sierpnia 2020). Themodynamika: proces adiabatyczny. Odzyskane z: Thoughtco.com
5. Devoe Howard i Neils Tom. (9 sierpnia 2020). Zmiany adiabatyczne. Chemia librettexts. Odzyskane z: chem.Librettexts.org