Teoretyczne prawdopodobieństwo, jak to wydostać, przykłady, ćwiczenia

Teoretyczne prawdopodobieństwo (lub laplace'a), że występuje zdarzenie, które należy do przestrzeni próbki, w której wszystkie zdarzenia mają takie samo prawdopodobieństwo wystąpienia, jest ono zdefiniowane w notacji matematycznej, takiej jak: p (e) = n (e) / n ( S)

Gdzie p (e) jest prawdopodobieństwem, podanym jako stosunek między całkowitą liczbą możliwych wyników zdarzenia e, które nazywamy n (e), podzielone przez całkowitą liczbę n (s) możliwych wyników w przestrzeni próbki s.

Rysunek 1. Podczas uruchomienia kości sześcioosobowej teoretyczne prawdopodobieństwo, że twarz z trzema kropkami znajduje się na górze. Źródło: Pixabay.

Prawdopodobieństwo teoretyczne jest liczbą rzeczywistą między 0 a 1, ale jest często wyrażana w postaci procentu, w którym to przypadku prawdopodobieństwo będzie wartością od 0% do 100%.

Obliczenie prawdopodobieństwa wystąpienia zdarzenia jest bardzo ważne w wielu dziedzinach, takich jak działalność giełdowa, firmy ubezpieczeniowe, hazard i wiele innych.

[TOC]

Jak uzyskać teoretyczne prawdopodobieństwo?

Przypadkiem ilustracyjnym jest przypadek Rifas lub Lotterie. Załóż, że 1.000 biletów na smartfon Rifar A. Ponieważ loteria jest wykonywana losowo, każdy z biletów ma taką samą szansę na zwycięzcę. 

Aby znaleźć prawdopodobieństwo, że osoba, która kupi bilet z zwycięzcą numeru 81, następujące obliczenia Teoretyczne prawdopodobieństwo:

P (1) = 1/1.000 = 0,001 = 0,1%

Poprzedni wynik jest interpretowany w następujący sposób: jeśli loteria jest powtarzana nieskończenie, co 1.000 razy bilet 81 zostanie wybrany średnio raz.

Jeśli z jakiegokolwiek powodu ktoś nabywa wszystkie bilety, jest pewien, że wygra nagrodę. Prawdopodobieństwo wygrania nagrody, jeśli masz wszystkie bilety obliczone w następujący sposób:

Może ci służyć: obwód krąg: jak go wybrać i formuły, rozwiązane ćwiczenia

P (1.000) = 1.000/1.000 = 1 = 100%.

To znaczy, jakie prawdopodobieństwo 1 lub 100% oznacza, że ​​jest całkowicie pewne, że ten wynik nastąpi.

Jeśli ktoś posiada 500 biletów, możliwości wygrania lub przegranej są takie same. Teoretyczne prawdopodobieństwo wygrania nagrody w tym przypadku jest obliczane w następujący sposób:

P (500) = 500/1.000 = ½ = 0,5 = 50%.

Ten, kto nie kupuje żadnego biletu, nie ma szans na wygraną, a jego teoretyczne prawdopodobieństwo jest zdeterminowane:

 P (0) = 0/1.000 = 0 = 0%

Przykłady

Przykład 1

Masz walutę z drogi z jednej strony i tarcza lub pieczęć w drugim. Po uruchomieniu waluty, jakie jest teoretyczne prawdopodobieństwo bycia drogim?

P (drogi) = n (drogi) / N ( twarz + tarcza ) = ½ = 0,5 = 50%

Wynik jest interpretowany w następujący sposób: jeśli dokonano ogromnej liczby wydawnict.

Pod względem procentowym interpretacja wyniku polega na tym, że dokonanie nieskończenie dużą liczbę premier, średnio co 100 z nich 50 spowodowałoby drogie.

Przykład 2

W pudełku znajdują się 3 niebieskie kulki, 2 czerwone kulki i 1 zielony. Jakie jest teoretyczne prawdopodobieństwo, że kiedy otrzymasz marmur z pudełka, jest czerwony?

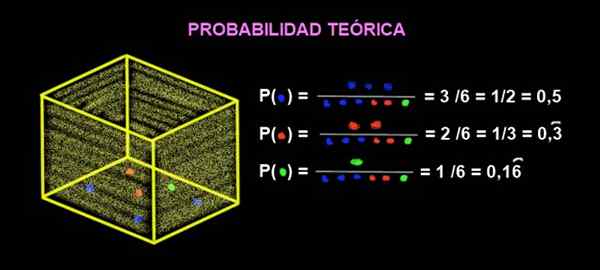Rysunek 2. Prawdopodobieństwo ekstrakcji kolorowych kul. Źródło: f. Zapata.

Prawdopodobieństwo, że pojawia się czerwona, to:

P (czerwony) = liczba korzystnych przypadków / liczba możliwych przypadków

To jest do powiedzenia:

P (czerwony) = liczba czerwonego kulki / całkowita liczba kulk

Wreszcie prawdopodobieństwo, że czerwony marmur wynosi:

P (czerwony) = 2/6 = ⅓ = 0,3333 = 33,33%

Podczas gdy prawdopodobieństwo, że przez wydobycie zielonego marmuru wynosi:

P (zielony) = ⅙ = 0,1666 = 16,66%

Wreszcie teoretyczne prawdopodobieństwo uzyskania w ślepej ekstrakcji niebieski marmur to: 

P (niebieski) = 3/6 = ½ = 0,5 = 50%

Może ci służyć: radykalne właściwości

Oznacza to, że z każdej 2 prób wynik będzie niebieski w jednym z nich, a inny kolor w innej próbie, pod założeniem, że wydobyty marmur jest uzupełniany i że liczba prób jest bardzo, bardzo duża, bardzo duża.

Ćwiczenia

Ćwiczenie 1

Określ prawdopodobieństwo, że podczas uruchamiania kostki wartość jest uzyskiwana mniejsza lub równa 4.

Rozwiązanie

Aby obliczyć prawdopodobieństwo wystąpienia tego zdarzenia, zastosuje się definicja prawdopodobieństwa teoretycznego:

P (≤4) = liczba korzystnych przypadków / liczba możliwych przypadków

P (≤5) = 5/6 = = 83,33%

Ćwiczenie 2

Znajdź prawdopodobieństwo, że na dwóch kolejnych boiskach normalnych kostek sześcioosobowych, 2 razy 2 razy.

Rozwiązanie

Aby odpowiedzieć na to ćwiczenie, wygodnie jest zrobić zdjęcie, aby pokazać wszystkie możliwości. Pierwsza liczba wskazuje wynik pierwszej kości, a drugi wynik drugiego.

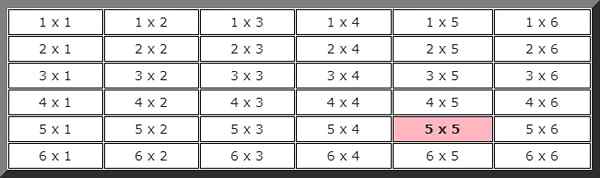
Aby obliczyć prawdopodobieństwo teoretyczne, musimy znać całkowitą liczbę możliwych przypadków, w tym przypadku, jak można zobaczyć z poprzedniej tabeli, istnieje 36 możliwości.

Obserwowanie obrazu wynika z tego, że liczba przypadków sprzyjających zdarzeniu, że w dwóch kolejnych wydaniach pojawia się 5, wynosi tylko 1, wyróżniony kolorem, dlatego prawdopodobieństwo, że to zdarzenie nastąpi, wynosi:

P (5 x 5) = 1/33.

Wynik ten można było również osiągnąć przy użyciu jednej z właściwości teoretycznego prawdopodobieństwa, który stwierdza, że ​​połączone prawdopodobieństwo dwóch niezależnych zdarzeń jest wynikiem ich indywidualnych prawdopodobieństw.

W tym przypadku prawdopodobieństwo, że w pierwszym wydaniu 5 wynosi ⅙. Drugie uruchomienie jest całkowicie niezależne od pierwszego, dlatego prawdopodobieństwo, że 5 w drugim wynosi również ⅙. Zatem połączone prawdopodobieństwo to:

Może ci służyć: częściowe pochodne: właściwości, obliczenia, ćwiczenia

P (5 × 5) = p (5) p (5) = (1/6) (1/6) = 1/36.

Ćwiczenie 3

Znajdź prawdopodobieństwo, że liczba mniejsza niż 2 wyjdzie w pierwszej premiery, aw drugiej wychodzi liczba większa niż 2. 

Rozwiązanie

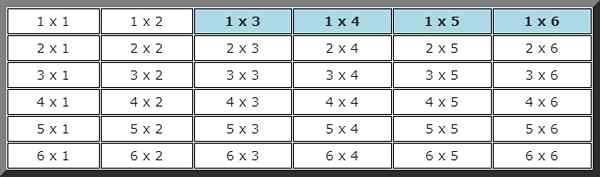
Znowu musisz zbudować możliwy tabel.

W sumie istnieje 4 możliwości łącznie 36. Innymi słowy, prawdopodobieństwo tego zdarzenia jest:

P (2) = 4/36 = 1/9 = 0,1111 = 11,11%

Wykorzystując twierdzenie o prawdopodobieństwie, które stwierdza:

Prawdopodobieństwo wystąpienia dwóch niezależnych zdarzeń jest równe iloczynowi poszczególnych prawdopodobieństw.

Jest uzyskiwany identyczny wynik:

P (2) = (1/6) (4/6) = 4/36 = 0,1111 = 11,11%

Wartość uzyskana w tej procedurze pokrywa się z poprzednim wynikiem, poprzez teoretyczną lub klasyczną definicję prawdopodobieństwa.

Ćwiczenie 4

Jakie jest prawdopodobieństwo, że uruchomienie dwóch, biorąc pod uwagę sumę wartości to 7.

Rozwiązanie

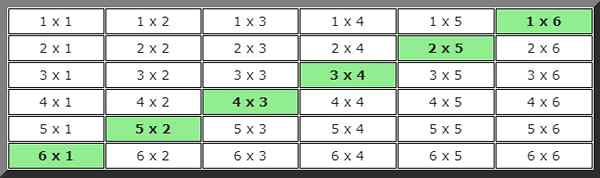
Aby znaleźć rozwiązanie w tym przypadku, opracowano obraz możliwości, w którym przypadki spełniające stan wartości wynoszą 7, wskazano w kolorze.

Patrząc na tabelę, można policzyć 6 możliwych przypadków, więc prawdopodobieństwo jest:

P (R&D II: 7) = 6/36 = 1/6 = 0,1666 = 16,66%

Bibliografia

1. Canavos, G. 1988. Prawdopodobieństwo i statystyki: Zastosowania i metody. McGraw Hill.
2. Devore, J. 2012. Prawdopodobieństwo i statystyki inżynierii i nauki. 8. Wydanie. Cengage.
3. Lipschutz, s. 1991. Seria Schaum: prawdopodobieństwo. McGraw Hill.
4. Obregón, i. 1989.Teoria prawdopodobieństwa. Limusa redakcyjna.
5. Walpole, r. 2007. Prawdopodobieństwo i statystyki inżynierii i nauki. osoba.