Koncepcja prawdopodobieństwa częstotliwości, jak oblicza się i przykłady

Prawdopodobieństwo częstotliwości jest substefinicja w ramach badania prawdopodobieństwa i jego zjawisk. Jego metoda badania w odniesieniu do zdarzeń i atrybutów opiera się na dużych ilościach iteracji, obserwując w ten sposób każde w perspektywie długoterminowej, a nawet nieskończonymi powtórzeniami.

Na przykład koperta gummitan zawiera 5 gałek każdego koloru: niebieski, czerwony, zielony i żółty. Chcesz określić prawdopodobieństwo, że każdy kolor musi odejść po losowym wyborze.

Źródło: Pexels

Nudne jest wyobrażenie sobie, że zdobycie gumy, nagrywanie, zwrot, wyjmowanie gumy i powtarzanie tego samego kilkaset lub kilkaset razy. Możesz nawet przestrzegać zachowania po kilku milionach iteracji.

Ale wręcz przeciwnie, interesujące jest odkrycie, że po kilku powtórzeniach oczekiwane prawdopodobieństwo 25% nie jest w pełni spełnione, przynajmniej nie dla wszystkich kolorów po wystąpieniu 100 iteracji.

Zgodnie z podejściem prawdopodobieństwa częstotliwości alokacja wartości będzie tylko poprzez badanie wielu iteracji. W ten sposób proces należy przeprowadzić i najlepiej zarejestrować w sposób skomputeryzowany lub naśladowany.

Wiele prądów odrzuca prawdopodobieństwo częstotliwości, argumentując brak empirycyzmu i wiarygodność w losowych kryteriach.

[TOC]

Jak obliczono prawdopodobieństwo częstotliwości?

Podczas programowania eksperymentu w dowolnym interfejsie zdolnym do oferowania czysto losowej iteracji, możesz zacząć badać prawdopodobieństwo częstotliwości tego zjawiska za pomocą tabeli wartości.

Poprzedni przykład jest doceniany na podstawie podejścia częstotliwości:

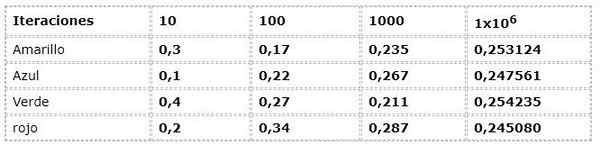
Dane numeryczne odpowiadają wyrażeniu:

N (a) = liczba wystąpień/ liczba iteracji

Gdzie n (a) reprezentuje względną częstotliwość zdarzenia „a”

„A” należy do zestawu możliwych wyników lub przestrzeni próbki ω

Może ci służyć: wielokrotności 8: co to jest i wyjaśnienie

Ω: czerwony, zielony, niebieski, żółty

W pierwszych iteracjach występuje znaczna dyspersja, gdy obserwuje się częstotliwości z nawet 30% różnic, co jest bardzo wysokim faktem dla eksperymentu, że teoretycznie ma zdarzenia o tej samej możliwości (EquipRobable).

Ale w miarę wzrostu iteracji wartości wydają się coraz bardziej dla tych przedstawionych przez prąd teoretyczny i logiczny.

Prawo wielkich liczb

Jako nieoczekiwane porozumienie między metodami teoretycznymi i częstotliwościami, powstaje prawo dużej liczby. Gdzie ustalono, że po znacznej ilości iteracji wartości eksperymentu częstotliwościowego zbliżają się do wartości teoretycznych.

W przykładzie można zauważyć, w jaki sposób wartości są przybliżone do 0,250, ponieważ iteracje rosną. Zjawisko to jest podstawowe w wnioskach wielu prac probabilistycznych.

Źródło: Pexels

Inne podejścia prawdopodobieństwa

Istnieją kolejne 2 teorie lub podejścia do pojęcia prawdopodobieństwa oprócz Prawdopodobieństwo częstotliwości.

Teoria logiczna

Twoje podejście jest zorientowane na dedukcyjną logikę zjawisk. W poprzednim przykładzie prawdopodobieństwo uzyskania każdego koloru jest zamknięte 25%. Innymi słowy.

Teoria subiektywna

Opiera się na wiedzy i wcześniejszych przekonaniach, które każda osoba ma na temat zjawisk i atrybutów. Oświadczenia takie jak "Zawsze pada deszcz podczas świętego tygodnia ” Posługują się wzorem podobnych zdarzeń, które miały miejsce wcześniej.

Historia

Początki jego wdrożenia po dziewiętnastym wieku, kiedy cytuję go w kilku swoich pracach w Cambridge England. Ale dopiero w XX wieku 2 matematyka statystyczna rozwinęła się i ukształtowała Prawdopodobieństwo częstotliwości.

Może ci służyć: równania wielomianowe

Jednym z nich był Hans Reichenbach, który rozwija swoją pracę w publikacjach takich jak „teoria prawdopodobieństwa” opublikowana w 1949 roku.

Drugim był Richard von Mises, który dokładniej rozwinął swoją pracę poprzez wiele publikacji i zaproponował, aby rozważyć prawdopodobieństwo za naukę matematyczną. Ta koncepcja była nowa w matematyce i oznaczałaby początek ery wzrostu w badaniu Prawdopodobieństwo częstotliwości.

Właściwie to wydarzenie robi jedyną różnicę w przypadku wkładu pokolenia Venna, Counta i Helm. Gdzie prawdopodobieństwo staje się odpowiednikiem, takim jak geometria i mechanika.

< La teoría de las probabilidades trata con masowe zjawiska i powtarzające się zdarzenia. Problemy, w których albo to samo zdarzenie jest powtarzane wielokrotnie, lub jednocześnie zaangażowana jest duża liczba jednolitych elementów> Richard von Mises

Masowe zjawiska i powtarzające się zdarzenia

Trzy typy można sklasyfikować:

• Fizyka: wzorce natury obdozowej poza stanem losowym. Na przykład zachowanie cząsteczek elementu w próbce.
• Szansa: jego fundamentalną kwestią jest losowość, ponieważ poprzez wielokrotne uwalnianie kości.
• Statystyka biologiczna: Wybór przedmiotów testowych zgodnie z ich cechami i atrybutami.

W teorii osoba, która mierzy, odgrywa rolę w danych probabilistycznych, ponieważ to jego wiedza i doświadczenia wyrażają tę wartość lub prognozę.

w Prawdopodobieństwo częstotliwości Wydarzenia będą uważane za kolekcje do leczenia, w których jednostka nie odgrywa żadnej roli w oszacowaniu.

Atrybuty

W każdym elemencie występuje atrybut, który będzie zmienny w zależności od charakteru tego. Na przykład w rodzaju zjawiska fizycznego cząsteczki wody będą miały różne prędkości.

Może ci służyć: trójkątne kryteria podobieństwa

Podczas uruchomienia kości znamy przestrzeń próbki ω, która reprezentuje atrybuty eksperymentu.

Ω: 1, 2, 3, 4, 5, 6

Istnieją inne atrybuty, takie jak ω_P  lub bądź dziwny ω_Siema

Ω_P : 2, 4, 6

Ω_Siema : 1, 3, 5

Które można zdefiniować jako atrybuty nie -elementarne.

Przykład

• Chcesz obliczyć częstotliwość każdej możliwej suma podczas uruchomienia dwóch kości.

W tym celu zaprogramowano eksperyment, w którym w każdej iteracji dodaje się dwie losowe wartości między [1, 6].

Dane są rejestrowane w tabeli i badane są trendy w dużych liczbach.

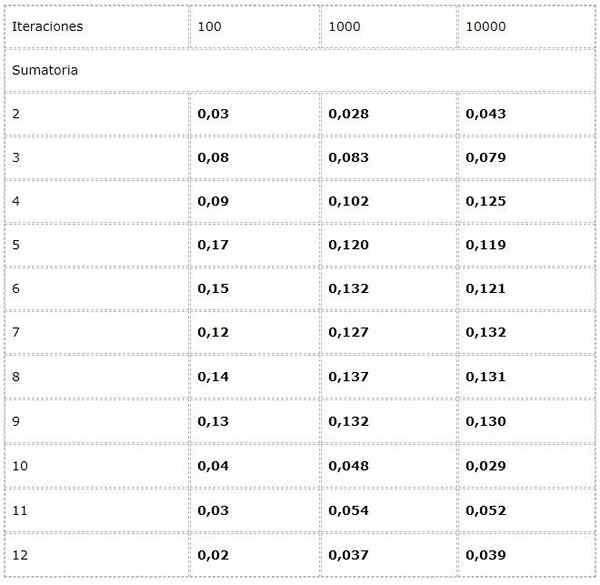
Zaobserwowano, że wyniki mogą się znacznie różnić między iteracji. Jednak prawo dużych liczb można zobaczyć w pozornej konwergencji przedstawionej w dwóch ostatnich kolumnach.

Bibliografia

1. Statystyki i ocena dowodów dla naukowców kryminalistycznych. Druga edycja. Colin g.G. Aitken. School of Mathematics. University of Edinburgh, Wielka Brytania
2. Matematyka informatyki. Eric Lehman. Google Inc.
   F Thomson Leighton Department of Mathematics and the Computer Science and AI Laboratory, Massachussetts Institute of Technology; Akamai Technologies
3. Nauczyciel arytmetyczny, tom 29. National Council of Teachers of Mathematics, 1981. Michigan University.
4. Uczenie się i nauczanie teoria numerów: badania poznania i nauczania / zredagowane przez Stephen R. Campbell i Rina Zazkis. Publish Publishing 88 Post Road West, Westport CT 06881
5. Bernoulli, J. (1987). Ars się podobieństwo- 4ème partie. Rouen: Irem.