Warunkowy wzór prawdopodobieństwa i równania, właściwości, przykłady

warunkowe prawdopodobieństwo Jest to możliwość wystąpienia pewnego zdarzenia, ponieważ inne występuje jako warunek. Te dodatkowe informacje mogą modyfikować (a może nie) przekonanie, że coś się wydarzy.

Na przykład możemy zadać sobie pytanie: „Jakie jest prawdopodobieństwo, że pada dziś, ponieważ dwa dni temu nie pada deszcz?". Wydarzenie, którego chcemy poznać prawdopodobieństwo, że pada dziś, a dodatkowe informacje, które stanowiłyby odpowiedź, brzmi: „Dwa dni temu nie pada”.

Rysunek 1. Prawdopodobieństwo, że pada dziś, ponieważ wczoraj padał wczoraj, jest również przykładem warunkowego prawdopodobieństwa. Źródło: Pixabay.

Być Przestrzeń probabilistyczna złożone z ω (przestrzeń próbki), ℬ (zdarzenia losowe) i p (prawdopodobieństwo każdego zdarzenia), a także zdarzenia A i B, które należą do ℬ.

Uwarunkowane prawdopodobieństwo, które nastąpi, ponieważ B, które jest oznaczone jako P (A│B), jest zdefiniowane w ten sposób:

P (a│b) = p (a∩b) / p (b) = p (a i b) / p (b)

Gdzie: p (a) jest prawdopodobieństwem występowania a, p (b) jest prawdopodobieństwo zdarzenia b i różni się od 0, a p (a∩b) jest prawdopodobieństwem przecięcia między A i B, to znaczy , prawdopodobieństwo wystąpienia obu zdarzeń (prawdopodobieństwo wspólne).

Jest to wyrażenie twierdzenia Bayesa zastosowane do dwóch wydarzeń, zaproponowanych w 1763 r. Przez angielskiego teologa i matematyka Thomasa Bayesa.

[TOC]

Nieruchomości

-Całe warunkowe prawdopodobieństwo wynosi od 0 do 1:

0 ≤ p (A│B) ≤ 1

-Prawdopodobieństwo, że zdarzenie nastąpi, ponieważ wydarzenie to nastąpi, wynosi oczywiście 1:

P (a│a) = p (a∩a) / p (a) = p (a) / p (a) = 1

-Jeśli dwa zdarzenia są wyłączne, to znaczy zdarzenia, które nie mogą się zdarzyć jednocześnie, to warunkowe prawdopodobieństwo, że jedno z nich się wydarzy, wynosi 0, ponieważ przecięcie jest nieważne:

P (a│b) = p (a∩b) / p (b) = 0 / p (b) = 0

-Jeśli B jest podzbiorem A, wówczas prawdopodobieństwo warunkowe wynosi również 1:

Może ci służyć: toroid lub toro dona

P (b│a) = p (a∩b) / p (a) = 1

Ważny

P (a│b) Zasadniczo nie jest równe P (B│A), dlatego musisz uważać, aby nie wymieniać zdarzeń podczas znajdowania warunkowego prawdopodobieństwa.

Ogólna zasada mnożenia

Wiele razy chcesz znaleźć wspólne prawdopodobieństwo p (a∩b), zamiast prawdopodobieństwa warunkowego. Tak więc, poprzez następujące twierdzenie:

P (a∩b) = p (a i b) = p (a│b). P (b)

Twierdzenie można rozszerzyć na trzy wydarzenia A, B i C:

P (a∩b∩c) = p (a i b i c) = p (a) · p (b│a) · p (c│a∩b)

A także na kilka wydarzeń, takich jak₁, DO₂, DO₃ A więcej, można go wyrazić w następujący sposób:

P (a₁∩ a₂ ∩ a₃… ∩ A_N) = P (a₁) . P (a₂│a₁). P (a₃│a₁∩ a₂) ... P (a_N│a₁∩ a₂∩… a_N-1)

Gdy jest to przypadek zdarzeń, które występują w sekwencji i na różnych etapach, wygodne jest zorganizowanie danych na schemacie lub tabeli. Ułatwia to wizualizację opcji osiągnięcia wymaganego prawdopodobieństwa.

Przykładami tego są schemat drzewa i Tabela awaryjna. Z jednego z nich możesz zbudować drugi.

Przykłady warunkowego prawdopodobieństwa

Spójrzmy na niektóre sytuacje, w których prawdopodobieństwo zdarzenia są zmieniane przez wystąpienie innego:

- Przykład 1

W słodkim sklepie sprzedawane są dwa rodzaje ciast: truskawki i czekolada. Podczas rejestracji preferencji 50 klientów obu płci ustalono następujące wartości:

-27 kobiet, z czego 11 woli truskawkowe i 16 ciasto czekoladowe.

-23 mężczyzn: 15 czekolady i 8 truskawek.

Prawdopodobieństwo, że klient wybierze ciasto czekoladowe, można ustalić, stosując zasadę Laplace'a, zgodnie z którą prawdopodobieństwo dowolnego zdarzenia wynosi:

P = liczba korzystnych zdarzeń/całkowita liczba zdarzeń

W takim przypadku 50 klientów w sumie 31 woli czekoladę, tak aby prawdopodobieństwo wyniosło p = 31/50 = 0.62. To znaczy 62% klientów woli ciasto czekoladowe.

Może ci służyć: równania wielomianowe

Ale czy byłby inaczej, gdyby klient jest kobietą? Jest to przypadek warunkowego prawdopodobieństwa.

Tabela awaryjna

Za pomocą takiego stolika awaryjnego sumy można łatwo wizualizować:

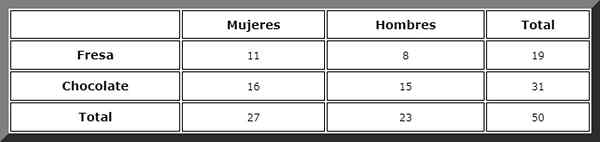
Następnie obserwowane są korzystne przypadki i stosuje się zasadę Laplace'a, ale zanim zdefiniujemy zdarzenia:

-B jest wydarzeniem „klienta kobiet”.

-A to wydarzenie „wolą ciasto czekoladowe” jako kobieta.

Przechodzimy do kolumny oznaczonej jako „kobiety” i tam widzimy, że suma to 27.

Następnie w rzędu „czekolady” poszukiwana jest korzystna obudowa. Istnieje 16 wydarzeń, dlatego poszukiwane prawdopodobieństwo jest bezpośrednio:

P (a│b) = 16/27 = 0.5924

59.24 % kobiet woli ciasto czekoladowe.

Ta wartość pokrywa się, gdy kontrastujemy z początkowo podaną definicją prawdopodobieństwa warunkowego:

P (a│b) = p (a∩b) / p (b)

Zapewniamy siebie poprzez zasadę Laplace'a i wartości tabeli:

P (b) = 27/50

P (a i b) = 16/50

Gdzie p (a i b) jest prawdopodobieństwem, że klient preferuje czekoladę i jest kobietą. Teraz wartości są zastąpione:

P (a│b) = p (a i b)/p (b) = (16/50)/(27/50) = 16/27 = 0.5924.

I udowodniono, że wynik jest taki sam.

- Przykład 2

W tym przykładzie stosuje się zasada mnożenia. Załóżmy, że na wystawie sklepu znajdują się spodnie w trzech rozmiarach: małe, średnie i duże.

W dużej mierze z 24 spodniami, z których jest 8 z każdej wielkości i wszystkie są mieszane. Jakie byłoby prawdopodobieństwo wydobycia dwóch z nich i że oba były małe?

Oczywiste jest, że prawdopodobieństwo wydobywania małych spodni w pierwszej próbie wynosi 8/24 = 1/3. Teraz druga ekstrakcja jest uwarunkowana do pierwszego wydarzenia, ponieważ kiedy wyjmujesz spodnie, nie ma już 24, ale 23. A jeśli małe spodnie zostaną usunięte, jest 7 zamiast 8.

Może ci służyć: Zasada multiplikatywna: Techniki zliczania i przykłady

Wydarzenie A polega na wyjęciu małych spodni, po zabraniu kolejnej w pierwszej próbie. A wydarzenie B to małe spodnie do pierwszego. Dlatego:

P (b) = 1/3; P (a│b) = 7/24

Wreszcie, poprzez zasadę mnożenia:

P (a∩b) = (7/24).(1/3) = 7/72 = 0.097

Ćwiczenie rozwiązane

W badaniu punktualności na komercyjnych lotach powietrznych dostępne są następujące dane:

-P (b) = 0.83, to prawdopodobieństwo, że samolot przyjmuje w odpowiednim czasie.

-P (a) = 0.81, to prawdopodobieństwo lądowania na czas.

-P (B∩A) = 0.78 Jest prawdopodobieństwo, że lot pojawi się na czas, biorąc czas.

Poproszono o obliczenie:

a) Jakie jest prawdopodobieństwo, że samolot wyląduje niezwłocznie, ponieważ wystartował na czas?

b) Powyższe prawdopodobieństwo jest takie samo, jak prawdopodobieństwo, że wyszło na czas, jeśli udało ci się wylądować niezwłocznie?

c) i wreszcie: jakie jest prawdopodobieństwo, że nadejdzie na czas, ponieważ nie pojawił się na czas?

Rysunek 2. Punktualność podczas lotów komercyjnych jest ważna, ponieważ opóźnienia generują straty milionera. Źródło: Pixabay.

Rozwiązanie

Aby odpowiedzieć na pytanie, stosuje się definicję prawdopodobieństwa warunkowego:

P (a│b) = p (a∩b) / p (b) = p (a i b) / p (b) = 0.78/0.83 = 0.9398

Rozwiązanie b

W takim przypadku zdarzenia są wymieniane w definicji:

P (b│a) = p (a∩b) / p (a) = p (a i b) / p (a) = 0.78/0.81 = 0.9630

Zauważ, że to prawdopodobieństwo nieco różni się od poprzedniej, jak wcześniej wskazaliśmy.

Rozwiązanie c

Prawdopodobieństwo braku punktu wynosi 1 - p (b) = 1 - 0,83 = 0.17, nazwiemy to P (B^C), Ponieważ jest to uzupełniające się wydarzenie, które można zająć czasem. Poszukiwane prawdopodobieństwo warunkowe jest:

P (a│b^C) = P (a∩b^C) / P (B^C) = P (a i b^C)/P (B^C)

Z drugiej strony:

P (a∩b^C) = P (lądowanie czasu) - p (lądowanie czasu i zerknięcie start) = 0.81-0.78 = 0.03

W takim przypadku poszukiwane prawdopodobieństwo to:

P (a│b^C) = 0.03/0.17 = 0.1765

Bibliografia

1. Canavos, G. 1988. Prawdopodobieństwo i statystyki: Zastosowania i metody. McGraw Hill.
2. Devore, J. 2012. Prawdopodobieństwo i statystyki inżynierii i nauki. 8. Wydanie. Cengage.
3. Lipschutz, s. 1991. Seria Schaum: prawdopodobieństwo. McGraw Hill.
4. Obregón, i. 1989.Teoria prawdopodobieństwa. Limusa redakcyjna.
5. Walpole, r. 2007. Prawdopodobieństwo i statystyki inżynierii i nauki. osoba.
6. Wikipedia. Uwarunkowane prawdopodobieństwo. Odzyskane z: jest.Wikipedia.org.