Heptagonowy pryzmat
- 4600
- 928
- Gabriela Łuczak
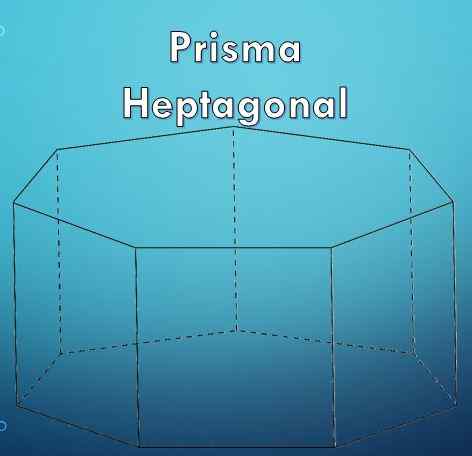
 Heptagonowy pryzmat ma 7 stron
Heptagonowy pryzmat ma 7 stron Co to jest heptagonowy pryzmat?
A heptagonowy pryzmat Jest to liczba geometryczna, która, jak sama nazwa wskazuje, obejmuje dwie definicje geometryczne: pryzmat i heptagon. „Prism” jest ograniczoną postacią geometryczną przez dwie podstawy, które są równe i równoległe wielokąty, a ich boczne twarze są równoległobokami.
„Heptagon” to wielokąt, który jest utworzony przez siedem (7) stron. Ponieważ heptagon jest wielokątem, może być konieczne regularne lub nieregularne.
Mówi się, że wielokąt jest regularny, jeśli wszystkie ich boki mają taką samą długość, a ich wewnętrzne kąty mierzą tak samo, nazywane są również wielokątami równobocznymi; W przeciwnym razie mówi się, że wielokąt jest nieregularny.

Charakterystyka heptagonowego pryzmatu
Poniżej znajdują się pewne cechy, które mają heptagonowy pryzmat, taki jak: jego budowa, właściwości baz, obszar wszystkich twarzy i objętość.
1- Budowa
Aby zbudować heptagonowy pryzmat, konieczne są dwa heptagony, które będą jego bazami i siedem równoległoboków, po jednym z każdej strony heptagonu.
Zaczyna rysować heptagon, a następnie rysuje siedem pionowych linii o tej samej długości, które pozostawiają z każdego z jego wierzchołków.
Wreszcie, kolejny heptagon jest narysowany w taki sposób, że jego wierzchołki pokrywają się z końcem linii narysowanych w poprzednim kroku.
Wcześniej narysowany heptagonowy pryzmat nazywa się prostym heptagonowym pryzmatem. Ale możesz także mieć skośny heptagonowy pryzmat, taki jak następująca liczba.
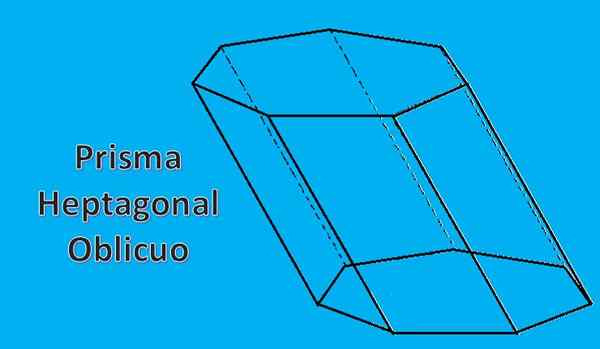
2- właściwości jego baz
Ponieważ ich podstawy są heptogonami, spełniają, że liczba przekątna wynosi d = nx (n-3)/2, gdzie „n” jest liczbą boków wielokąta; W takim przypadku musisz d = 7 × 4/2 = 14.
Może ci służyć: jakie są trójkątne liczby? Właściwości i demonstracjeWidzimy również, że suma wewnętrznych kątów dowolnego heptagonu (regularnego lub nieregularnego) jest ta sama 900 °. Można to sprawdzić za pomocą następującego obrazu.
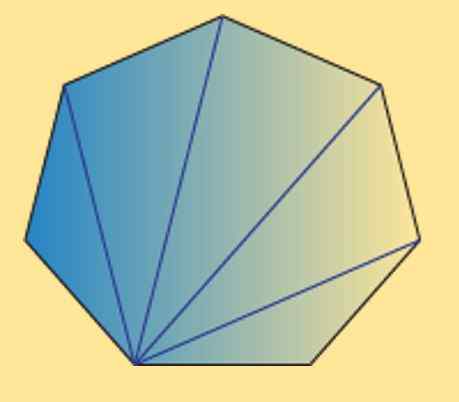
Jak widać, istnieje 5 wewnętrznych trójkątów, a przy użyciu sumie wewnętrznych kąta trójkąta jest równa 180 °, można uzyskać, że pożądany wynik.
3- Obszar niezbędny do zbudowania heptagonowego pryzmatu
Ponieważ jego podstawą są dwa heptogony, a jego boki to siedem równoległoboków, obszar niezbędny do budowy pryzmatu heptagonowego jest równy 2xh+7xp, gdzie „h” jest obszarem każdego heptagon równoległobok.

W tym przypadku obliczono obszar zwykłego heptagonu. Dla tego ważne jest, aby znać definicję apothem.
ApotheMe to linia prostopadła, która przechodzi od środka zwykłego wielokąta do punktu środkowego dowolnej strony.
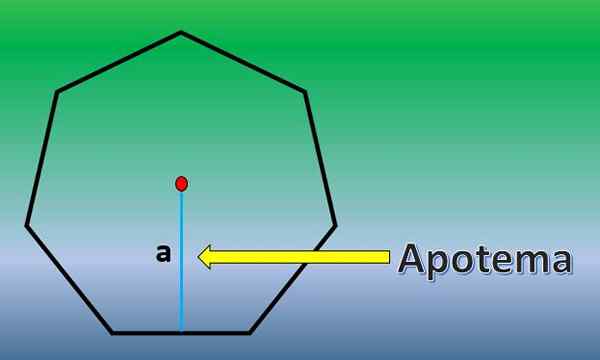
Gdy apoteme jest znane, obszar heptagonu wynosi h = 7xlxa/2, gdzie „l” to długość każdej strony i „a” długość apotemu.
Obszar równoległoboku jest łatwy do obliczenia, jest zdefiniowany jako p = lxh, gdzie „l” jest tą samą długością strony heptagonu, a „h” jest wysokością pryzmatu.
Podsumowując, ilość materiału potrzebnego do budowy pryzmatu heptagonowego (ze zwykłymi zasadami) wynosi 7xlxa+7xlxh, to znaczy 7xl (a+h).
4- Tom
Gdy obszar podstawy i wysokość pryzmatu jest znana, objętość jest zdefiniowana jako (obszar podstawowy) x (wysokość).
W przypadku heptagonowego pryzmatu (z regularną podstawą) musi to być v = 7xlxaxh/2; Można go również zapisać jako v = pxaxh/2, gdzie „p” jest obwodem zwykłego heptagonu.
Może ci służyć: jakie są dzielniki 30? (Wyjaśnienie)
