Historia zasad wielkanocnych, aplikacje, przykłady

On Zasada Pascal, o Pascal Prawo, ustala, że ​​zmiana ciśnienia płynu ograniczonego w dowolnym jego punktach jest przenoszona bez zmiany na wszystkie inne punkty w płynie.

Zasada ta została odkryta przez francuskiego naukowca Blaise Pascal (1623–1662). Ze względu na znaczenie wkładu Pascal na naukę, jednostka presji w systemie międzynarodowym została mianowana na jego cześć.

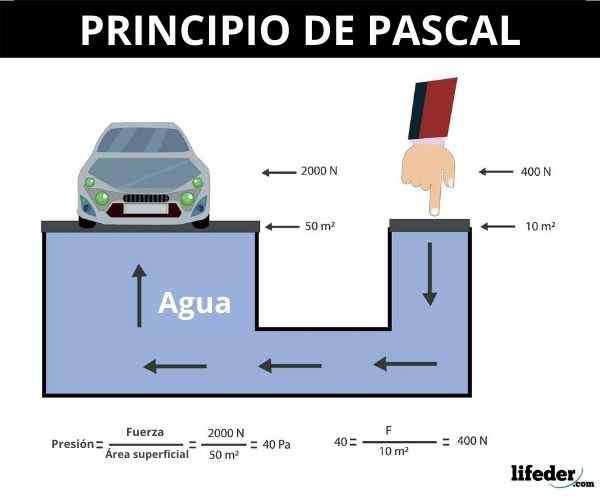
Ponieważ ciśnienie jest zdefiniowane jako iloraz między siłą prostopadłą do obszaru między jej obszarem, 1 Pascal (PA) równa się 1 Newton / m².

[TOC]

Historia

Aby zweryfikować jego zasadę, Pascal opracował dość przytłaczającą demonstrację. Wziął pustą kulę i przeszył w kilka miejscach, włożył czapki we wszystkich dziurach, z wyjątkiem jednego, dla którego napełnił ją wodą. W tym umieścił strzykawkę z tłokiem.

Wystarczającym zwiększenie ciśnienia w tłoku, czapki są strzelane w tym samym czasie, ponieważ ciśnienie jest przekazywane równo do wszystkich punktów płynu i we wszystkich kierunkach, pokazując w ten sposób prawo Pascal.

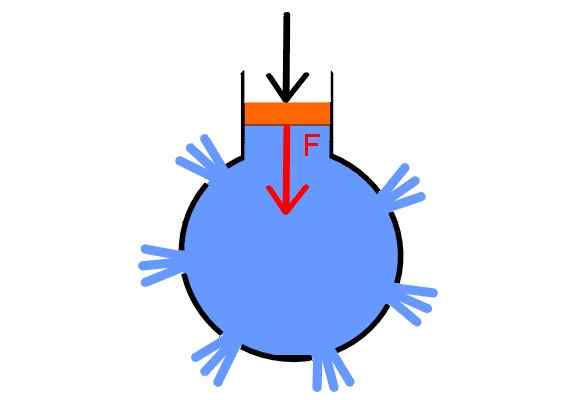Strzykawka Pascal. Źródło: Wikimedia Commons.

Blaise Pascal miał krótkie życie, naznaczone chorobą. Niesamowity zasięg jego umysłu doprowadził go do zbadania w różnych aspektach natury i filozofii. Jego wkład nie ograniczył się do badania zachowania płynów, Pascal był również pionierem obliczeń.

W wieku 19 lat Pascal stworzyła mechaniczny kalkulator dla jej ojca, aby wykorzystał ją w jej pracy we francuskim systemie podatkowym: Pascalina.

Również wraz z jego przyjacielem i kolegą wielkim matematykiem Pierre z Fermat, ukształtował teorię prawdopodobieństwa, niezbędny w fizyce i statystyce. Pascal zmarł w Paryżu, w wieku 39 lat.

Wyjaśnienie zasady Pascal

Następny eksperyment jest dość prosty: rurka U jest wypełniona wodą, a czapki są umieszczane na każdym końcu, które mogą płynnie i łatwo przesuwać się jako tłok. Jest to nacisk na lewą tłok, a nieco obserwuje się, że ten po prawej podnosi się, popychany przez płyn (dolna liczba).

Może ci służyć: Andromeda: odkrycie, pochodzenie, cechy, struktura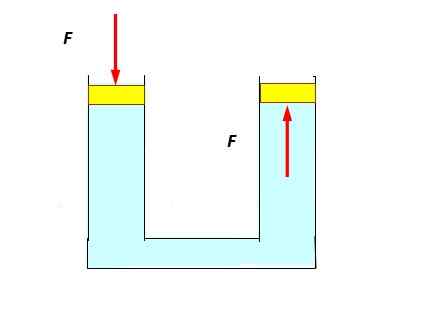Zastosowanie zasady Pascal. Źródło: Self Made.

Dzieje się tak, ponieważ ciśnienie jest przenoszone bez żadnego spadku do pełnego punktu płynu, w tym tych, które mają kontakt z prawym tłokiem.

Ciecze, takie jak woda lub olej, są nieściśliwa, ale jednocześnie cząsteczki mają wystarczającą swobodę ruchu, co umożliwia rozkład ciśnienia na prawym tłoku.

Dzięki temu prawy tłok otrzymuje siłę, która jest dokładnie taka sama pod względem wielkości i kierunku, do którego został przyłożony w lewo, ale w przeciwnym kierunku.

Ciśnienie w płynie statycznym jest niezależne od kształtu pojemnika. Zostanie natychmiast wykazane, że ciśnienie zmienia się liniowo w zależności od głębokości, a zasada Pascal jest konsekwencją tego.

Zmiana ciśnienia w dowolnym momencie, powoduje, że ciśnienie w innym punkcie zmienia się w tej samej ilości. W przeciwnym razie istniałoby dodatkowe ciśnienie, które przepłynęłoby ciecz.

Związek między ciśnieniem a głębokością

Płyn odpoczynkowy wywiera siłę na ścianki pojemnika, który go zawiera, a także na powierzchni dowolnego obiektu zanurzonego w nim. W eksperymencie strzykawki Pascal widać, że pojawia się woda pionowo Do kuli.

Płyny rozkładają siłę prostopadle na powierzchni, na której działa, więc wygodne jest wprowadzenie koncepcji średniego ciśnienia P_M Jak wywierała siła prostopadła F_⊥ Według obszaru DO, którego jednostką jest Pascal:

P_M = F_⊥ / DO

Ciśnienie wzrasta wraz z głębokością. Możesz zobaczyć małą część statycznego płynu równowagi i zastosować drugie prawo Newtona:

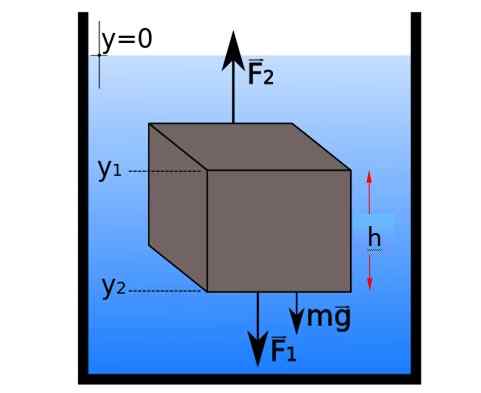Schemat wolnego ciała małej części równowagi statycznej z w kształcie kostki. Źródło: E-XUAO [CC BY-SA 4.0 (https: // creativeCommons.Org/licencje/nabrzeże/4.0)]

Siły poziome są anulowane przez pary, ale w kierunku pionowym siły są pogrupowane w następujący sposób:

∑F_I = F₂ - F₁ - Mg = 0 → F₂ - F₁ = mg

Wyrażanie ciasta pod względem gęstości ρ = ​​masa /objętość:

P₂.A- p₁.A = ρ X Tom x g

Objętość porcji płynów jest produktem w temperaturze X H:

Może ci służyć: drugie prawo termodynamiki: wzory, równania, przykłady

DO.(P₂ - P₁) = ρ X a x h x g

ΔP = ρ.G.H   Podstawowe twierdzenie hydrostatycznego

Aplikacje

Kolekko wykorzystuje zasadę Pascal do podnoszenia dużych pesos

Zasada Pascal została wykorzystana do budowy licznych urządzeń, które mnożą siłę i ułatwiają zadania, takie jak podnoszenie pesos, stemplowanie na metalowych lub prasujących obiektach. Wśród nich są:

-Prasa hydrauliczna

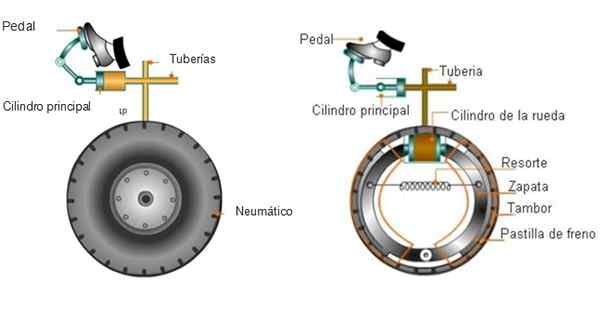
-Układ hamulca samochodu

-Łopaty mechaniczne i ramiona mechaniczne

-Hydrauliczny kot

-Żuty i windy

Następnie zobaczmy, w jaki sposób zasada Pascal sprawia, że ​​małe siły przekształca się w duże siły, aby wykonać wszystkie te prace. Prasa hydrauliczna jest najbardziej charakterystycznym przykładem i zostanie przeanalizowana poniżej.

Prasa hydrauliczna

Aby zbudować prasę hydrauliczną, zabrane jest to samo urządzenie górnej figury, to znaczy pojemnik w kształcie litery U, który już wiemy, że ta sama siła jest przesyłana z jednego tłoka. Różnica będzie miał rozmiar tłoków i to sprawia, że ​​urządzenie działa.

Poniższy rysunek pokazuje zasadę Pascal w działaniu. Ciśnienie jest takie samo we wszystkich punktach płynu, zarówno w małym, jak i dużych tłokach:

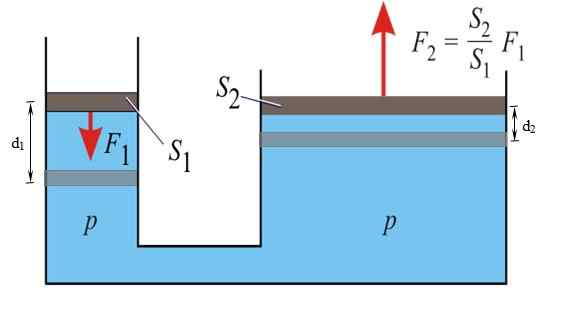Schemat prasy hydraulicznej. Źródło: Wikimedia Commons.

p = f₁ / S₁ = F₂ / S₂

Wielkość siły przenoszonej na duży tłok to:

F₂ = (S₂ / S₁). F₁

Lubi₂ > S₁, wyniki w f₂ > F₁, Dlatego siła wyjściowa pomnożyła się w współczynniku podanym przez iloraz między obszarami.

Przykłady

Ta sekcja pokazuje przykłady aplikacji.

Hydrauliczne hamulce

Hamulce samochodowe wykorzystują zasadę Pascal przez płyn hydrauliczny, który wypełnia niektóre rurki podłączone do kół. Kiedy musisz się zatrzymać, kierowca nakłada siłę, uciskając pedał hamulca i generowanie nacisku na płyn.

Na drugim końcu ciśnienie popycha podkładki hamulcowe o bęben lub dyski hamulcowe, które obracają się razem z kółkami (nie z oponami). Powstałe tarcie zatrzymuje się, a także spowalnia.

Może ci służyć: fale mechaniczne: cechy, właściwości, wzory, typyHydrauliczny układ hamulca. Źródło: f. Zapata

Mechaniczna przewaga prasy hydraulicznej

W prasie hydraulicznej dolnej figu.

Siła wejściowa F₁ sprawia, że ​​tłok podróżuje w odległość d₁ Podczas schodzenia, podczas gdy siła wyjściowa F₂ Pozwala na d₂ tłoka, który rośnie. Jeśli praca mechaniczna wykonana przez obie siły jest taka sama:

F₁.D₁ = F₂. D₂

Zaletą mechaniczną M jest iloraz między wielkościami siły wejściowej i wyjściowej:

M = f₂/F₁ = d₁/D₂

I jak pokazano w poprzedniej części, można go również wyrazić jako iloraz między obszarami:

F₂/F₁ = S₂ / S₁

Wygląda na to, że praca jest wykonywana za darmo, ale tak naprawdę nie tworzy energii z tym urządzeniem, ponieważ przewaga mechaniczna jest uzyskiwana kosztem przemieszczenia małego tłoka D₁.

Aby zoptymalizować wydajność, system zaworów jest dodawany do urządzenia w taki sposób, że tłok wyjściowy jest podniesiony dzięki krótkim impulsom tłoka wejściowego.

W ten sposób operator garażu hydrauliczne pompy kota kilkakrotnie, aby stopniowo podnosić pojazd.

Ćwiczenie rozwiązane

W prasie hydraulicznej na rycinie 5 obszary tłoków wynoszą 0.5 cali kwadratowych (mały tłok) i 25 cali kwadratowych (duży tłok). Znajdować:

a) Zaleta mechaniczna tej prasy.

b) niezbędna siła do podniesienia ładunku 1 tony.

c) odległość, z jaką siła wejściowa musi działać, aby podnieść wspomniane obciążenie w 1 cala.

Wyraź wszystkie wyniki w jednostkach systemu brytyjskiego i systemu międzynarodowego, jeśli.

Rozwiązanie

a) Zaletą mechaniczną jest:

M = f₂/F₁ = S₂/S₁ = 25 cali² / 0.5 cali² = 50

b) 1 ton równoważny 2000 funtów. Niezbędna siła to f₁:

F₁ = F₂ / M = 2000 funtów siła / 50 = 40 funtów siła

Aby wyrazić wynik w systemie międzynarodowym, wymagany jest następujący współczynnik konwersji:

1 funt-force = 4.448 n

Dlatego wielkość F1 wynosi 177.92 n.

C) M = D₁/D_{2 →} D₁ = M.D₂ = 50 x 1 in = 50 cali

Niezbędny współczynnik konwersji to: 1 cal = 2.54 cm

D₁ = 127 cm = 1.27 m

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill. 417-450.
2. Fizyka uczelni. Pascal's Principie. Odzyskane z: openTextBC.AC.
3. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 4. Płyny i termodynamika. Pod redakcją Douglas Figueroa (USB). 4 - 12.
4. Rex, a. 2011. Podstawy fizyki. osoba. 246-255.
5. Tippens, s. 1. 2011. Fizyka: koncepcje i zastosowania. 7. edycja. McGraw Hill.301-320.