Wzór ciśnienia hydrostatycznego, obliczenia, przykłady, ćwiczenia

Ciśnienie hydrostatyczne Jest to ten, który wywiera płyn w równowadze statycznej w dowolnym miejscu, albo zanurzony w nim obszar, ściany pojemnika lub część płynu, która jest częścią całkowitej masy.

Sposób, w jaki płyny wywierają ciśnienie, różni się od ciał stałych. Wywierają ciśnienie w dół, ale ciecz lub gaz robią to we wszystkich kierunkach.

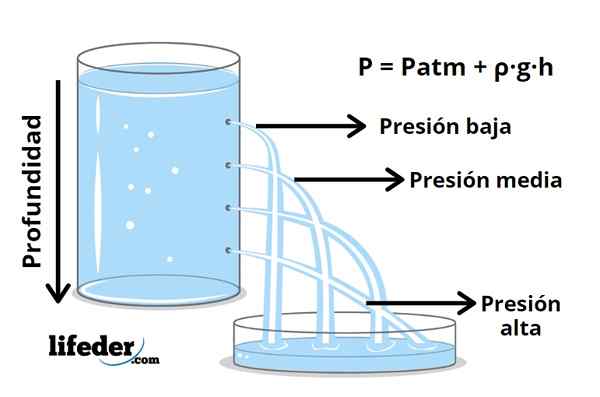
Rycina 1- Na większej głębokości większe ciśnienie

Jeśli chodzi o ciecz, ciśnienie wzrasta wraz z głębokością, o czym wiadomo z doświadczenia podczas zanurzenia w wodzie, w której odczuwa się wzrost ciśnienia w uszach. Ciśnienie to pochodzi z masy płynu i nieustannego ruchu cząstek, które go tworzą, które nieustannie uderzają w powierzchnię ciała zanurzoną w płynie.

Jeśli założymy nieściśliwą ciecz - co jest prawdziwe w zdecydowanej większości zastosowań, - jej gęstość pozostaje stała iw takim przypadku ciśnienie zależy liniowo od głębokości.

[TOC]

Formuła

Ciśnienie hydrostatyczne jest obliczane na podstawie następującego wyrażenia:

P = p_bankomat + ρ · g · h

Gdzie:

-P ciśnienie wywierało się w punkcie

-P_bankomat Jest to ciśnienie atmosfery na wolnej powierzchni

-ρ to gęstość płynów

-G to przyspieszenie grawitacji

-H to głębokość, na którą chcesz obliczyć ciśnienie hydrostatyczne 

Wzór obejmuje skutki atmosfery, ale wiele ciśnienia lub manometrów umieszcza 0 w ciśnieniu atmosferycznym, z tego powodu mierzą się różnicowa ciśnienie lub ciśnienie względne, zwane również ciśnienie miernika:

P_M = ρ · g · h

Jeśli chodzi o gazy, są one bardzo łatwo sprężane lub rozszerzane. Dlatego jego gęstość, która jest przyczyną między masą a objętością, jest zwykle funkcją innych parametrów, takich jak wysokość i temperatura, w przypadku gazów atmosferycznych.

Może ci służyć: magnetyzacja: moment magnetyczny orbital i spin, przykłady

Ciśnienie wywierane przez gazy jest zwykle wywoływane ciśnienie aerostatyczne, termin zarezerwowany ciśnienie hydrostatyczne dla cieczy.

Przykłady ciśnienia hydrostatycznego

Ciśnienie hydrostatyczne zależy tylko od głębokości, więc kształt lub obszar podstawy pojemnika nie jest istotny.

Ponieważ ciśnienie p jest zdefiniowane jako prostopadły składnik siły F na jednostkę obszaru A:

P = f/a

Wówczas siła wywierana przez ciecz na dole pojemnika może być inna, ale rozmieszczona na różnych rozszerzeniach, ciśnienie, które jest stosunkiem siły/powierzchni, jest taka sama dla punktów na tę samą głębokość.

Rozważ pojemniki z figury. Ciśnienie jest takie samo dla wszystkich czerwonych punktów, które są na tym samym poziomie, chociaż większa ilość płynu powyżej tego poziomu w centralnym pojemniku -więcej szerokości -których znajduje się cylindryczna i cienka rurka ekstremalnej lewicy.

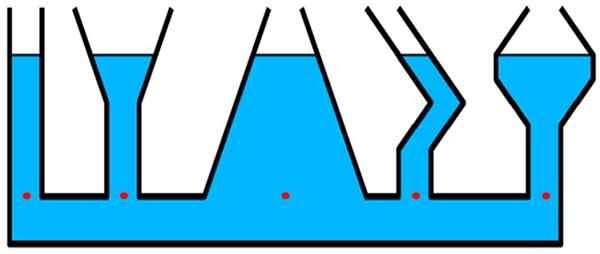Rysunek 2.- Ciśnienie w jednym z czerwonych punktów jest takie same, niezależnie od kształtu pojemnika. Źródło: Wikimedia Commons.

Struktury, w których istotne jest ciśnienie hydrostatyczne

-Ściany tamy: chociaż siła jest taka sama dla wszystkich punktów płaskiego dna, na pionowej ścianie rośnie wraz ze wzrostem głębokości, więc ściany oporowe są szersze w podstawie niż w górnej części.

-Na ścianach i dnie basenu.

-W gwiazdach takich jak nasze słońce, gdzie ciśnienie hydrostatyczne równoważy siłę grawitacji i utrzymuje gwiazdę w działaniu. Kiedy wspomniana równowaga jest złamana, gwiazda upada i cierpi ekstremalne zmiany w swojej strukturze.

Może ci służyć: jaki jest moment magnetyczny?

-Zbiorniki magazynowe cieczy, zaprojektowane w celu odporności na ciśnienie hydrostatyczne. Nie tylko ściany, ale bramy, które ułatwiają wypełnienie i ekstrakcję. Za jego projekt jest uwzględniający, jeśli ciecz jest żrący, a także ciśnienie i siła, którą wywiera zgodnie z jego gęstością.

-Opony i balony, które są zarażone w taki sposób, aby odporne na ciśnienie płynu (gaz lub ciecz) bez rozrywania.

-Wszelkie zanurzone ciało, które odczuwa pchnięcie pionowe lub „ulgę”, dzięki ciśnieniu hydrostatyczne wywierane przez ciek. Jest to znane jako Zasada Archimedesa.

Ćwiczenia

Zasada Archimedesa potwierdza, że ​​zanurzając ciało, całkowicie lub częściowo, doświadczy pionowej siły w górę, znanej jako ciąg. Wielkość ciągu jest liczbowo równa masy objętości wody wypieranej przez obiekt.

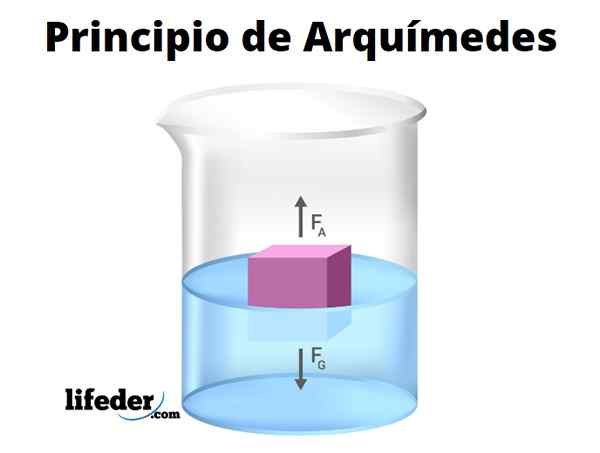
Być ρ_biegły Gęstość płynu, v_S Zanurzona objętość, przyspieszenie grawitacji i b wielkość ciągu, którą możemy obliczyć na następującym wyrażeniu:

B = ρ_biegły .V_S .G

- Ćwiczenie 1

Prostokątny blok, którego wymiary to 2.0 cm x 2.0 cm x 6.0 cm unosi się w słodkiej wodzie z najdłuższą osą pionową. Długość bloku, która wyróżnia się nad wodą, wynosi 2.0 cm. Oblicz gęstość bloku.

Rozwiązanie

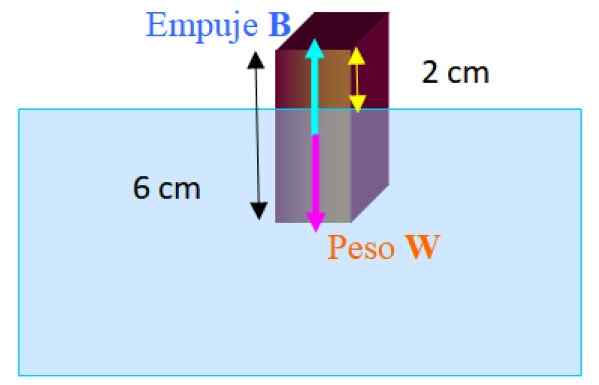Rysunek 3.- Schemat wolnego ciała dla bloku, który unosi się częściowo zanurzony w wodzie. Źródło: f. Zapata.

Siły działające na bloku to waga W w dół i pchnięcie B w górę. Gdy blok unosi się w równowadze:

∑ f_I = B - w = 0

B = w

Wielkość masy w jest iloczynem masy m bloku z powodu przyspieszenia grawitacji. Użyjemy definicji gęstości ρ_albo Jak iloraz między masą M i objętość V bloku:

Może Ci służyć: analiza zbiórki: koncepcje, metody, przykłady

ρ_albo = m / v → m = ρ_albo . V

Ze swojej strony ciąg wynosi:

B = ρ_biegły .V_S .G

Wyrównanie wielkości ciągu i wielkość wagi:

ρ_biegły .V_S .G = ρ_albo . V.G

Grawitacja jest anulowana jako czynnik po obu stronach, a gęstość bloku można wyczyścić jako:

ρ_albo = ρ_biegły . (V_S  / V)

Gęstość wody w międzynarodowych jednostkach systemowych wynosi 1000 kg/m³. Całkowite v tomy i zanurzone v_S, Są one obliczane przez v = szerokość x wysoką x głębokość:

V = 2.0 cm x 2.0 cm x 6.0 cm = 24.0 cm³

V_S = 2.0 cm x 2.0 cm x 4.0 cm = 16.0 cm³

Wymiana wartości:

ρ_albo = ρ_biegły . (V_S  / V) = 1000 kg/ m³ . (16/24) = 667 kg/m³

- Ćwiczenie 2

Oblicz zanurzony procent objętości kawałka lodu unoszącego się w wodzie morskiej na 0 ° C.

Rozwiązanie

Lód unosi się w wodzie, ponieważ jego gęstość jest niższa: 916.8 kg/m³, co oznacza, że ​​się rozszerza, gdy się ochłodzi, w przeciwieństwie do większości substancji, że po grzeszaniu zwiększają objętość.

Rysunek 4. Prawie cała ilość góry lodowej pozostaje zanurzona. Źródło: Pixabay.

Jest to bardzo szczęśliwa okoliczność na całe życie, od tego czasu masy wody zamrażają tylko na powierzchni, pozostając ciekłym w głębokości.

Gęstość wody morskiej jest nieco większa niż w przypadku świeżej wody: 1027 kg/m³. Oblikujemy ułamek objętości v_S  / V:

V_S  / V = ​​ρ_albo / ρ_biegły = 916.8 kg/m³  / 1027 kg/ m³ = 0.8927

Oznacza to, że około 89 % lodu pozostaje zanurzone pod wodą. Tylko 11 % jest widoczne unoszące się na morzu.

Bibliografia

1. Giambattista, a. 2010. Fizyka. 2. Wyd. McGraw Hill.
2. Knight, r.  2017. Fizyka dla naukowców i inżynierii: podejście strategiczne. osoba.
3. Cimbala, c. 2006. Mechanika płynów, podstaw i zastosowań. MC. Graw Hill.
4. Hibbeler, R. 2015. Mechanika płynów. 1st. Wyd. osoba.
5. Mott, r.  2006. Mechanika płynów. 4. Wydanie. Edukacja Pearsona.
6. Streeter, v. 1999. Mechanika płynów. McGraw Hill.