Regularne właściwości wielokąta, elementy, kąty, przykłady

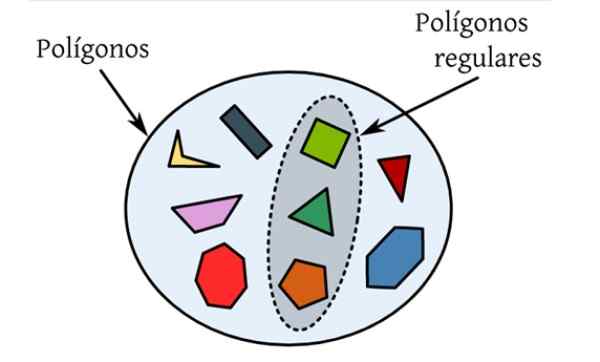
Zwykłe wielokąty Są tymi, którzy mają wszystkie swoje strony i równe kąty wewnętrzne. Na poniższym rysunku znajduje się zestaw różnych wielokątów, które są płaskie liczby ograniczone przez zamkniętą krzywą i tylko te, które są wyróżnione, spełniają warunki, które są regularne.

Na przykład trójkąt równoboczny jest regularnym wielokątem, ponieważ jego trzy strony mierzą tak samo, a także jego wewnętrzne kąty, które są warte 60 °.

Rysunek 1. Regularne wielokąty to te, których boki i kąty wewnętrzne są takie same, takie jak trójkąt równoboczny i kwadrat. Źródło: Wikimedia Commons.

Kwadrat jest czworoboczny z czterema bokami równej miary i których wewnętrzne kąty wynoszą 90º. Następnie następuje regularny Pentagon, z pięcioma stronami równej wielkości i pięcioma wewnętrznymi kątami o wartości 108º.

Kiedy wielokąt jest regularny, to słowo jest dodawane do jego specjalnej nazwy, dlatego mamy zwykły sześciokąt, zwykły heptagon i tak dalej.

[TOC]

Właściwości zwykłych wielokątów

Najważniejsze właściwości zwykłych wielokątów można podsumować w następujący sposób:

-Boki mierzą tak samo, dlatego są równoboje.

-Czy Równoznaczne, Cóż, wszystkie jego wewnętrzne kąty mają równą miarę.

-Zawsze mogą zarejestrować się w obwodzie, co oznacza, że ​​idealnie pasują do jednego, który się nazywa ograniczony obwód.

-W przypadku zwykłego wielokąta po bokach miara wewnętrznego kąta α wynosi:

α = [180 (n-2)]/n

-N-3)/2 przekątne można wyciągnąć z wierzchołków wielokąta, czy to regularne, czy nie.

-Suma Kąty zewnętrzne Jest równy 360º.

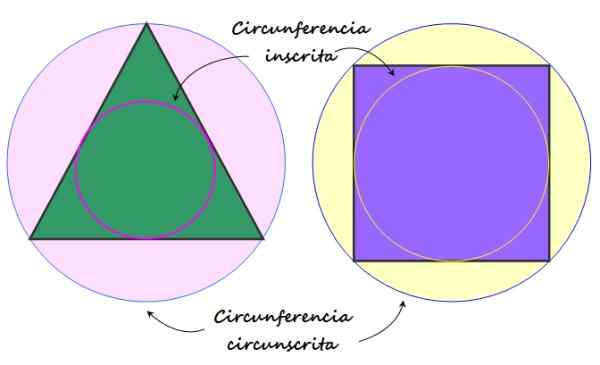Rysunek 2. Zarejestrowany obwód i obwód ograniczone do zwykłego wielokąta. Źródło: f. Zapata.

Elementy zwykłego wielokąta

Następnie przedstawiamy główne elementy zwykłego wielokąta, wizualizowane na dolnej figurze.

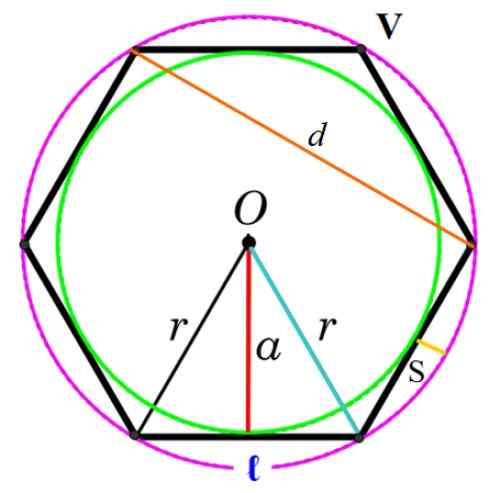Rysunek 3. Elementy zwykłego wielokąta. Źródło: f. Zapata.

Wierzchołek

Wspólny punkt, który ma dwie kolejne strony, oznaczone jako v na rysunku.

Strona

Jest to segment, który łączy dwa kolejne wierzchołki wielokąta i jest oznaczony jako ℓ lub l.

Przekątna

Segment, który dołącza do dwóch nieobserwowych wierzchołków wielokąta, na rysunku jest to oznaczone jako D.

Centrum

Jest to wspólne centrum zarejestrowanego obwodu i ograniczony obwód, oznaczony literą lub. Można go również postrzegać jako jedyny punkt, w którym równoznacz zarówno wierzchołków, jak i punktów środkowych z każdej strony.

Radio

To jest radio R ograniczonego obwodu i pokrywa się z odległością między O i wierzchołkiem.

Może ci służyć: aksjomaty prawdopodobieństwa: typy, wyjaśnienie, przykłady, ćwiczenia

Apothem

Nazywa się Apothem do promienia obwodu wpisanego w wielokąt, reprezentowany na rysunku literą Do. Apothem jest prostopadle do boku i łączy to ze środkiem O (czerwony segment na ryc. 3).

Znając promień r i długość boku, apothem jest obliczany przez:

Ponieważ w efekcie apothem jest jedną z kategorii trójkąta prostokąta (patrz ryc. 3), a drugie Cateto to wartość ℓ/2 (połowa jednej strony) i hipotenuy radiowe Radio R wielokąta.

Gdy do wspomnianego trójkąta stosuje się twierdzenie Pitagorasa, to równanie to jest ważne nie tylko dla sześciokąta, ale dla każdego zwykłego wielokąta.

Kąt centralny

Jest to kąt, którego wierzchołek zbiega się z centrum lub po czym są segmenty, które łączą centrum z dwoma kolejnymi wierzchołkami. Jego miara w stopniach seksualnych wynosi 360º/n, gdzie N Jest to liczba boków wielokąta.

Sagita

Jest to różnica między promieniem wielokąta a apotemem (patrz ryc. 3). Oznaczanie sagity jako s:

S = r - a

Obwód i obszar

Obwód

Można go łatwo obliczyć, dodając długości boków. Ponieważ każda strona ma tę samą długość l i istnieje n bok, obwód p wyraża się jako:

P = n.L

Obszar

W zwykłym wielokątach obszar A jest podany przez produkt między półperimetrem (połowa obwodu) a długością apotemu Do.

A = p.A /2

Ponieważ obwód zależy od liczby stron n, okazuje się, że:

A = (nl).A /2

Dwa zwykłe wielokąty mogą mieć ten sam obwód, nawet jeśli nie mają takiej samej liczby stron, ponieważ zależałoby to od długości boków.

W książce V twojego Kolekcja, Matematyk Pappus z Aleksandrii (290-350), ostatni z wielkich greckich matematyków starożytności, wykazał, że spośród wszystkich zwykłych wielokątów z tym samym obwodem, ten z największym obszarem jest ten z największą liczbą boków.

Kąty

Rycina 4 pokazuje odpowiednie kąty w zwykłym wielokąta, oznaczonym greckim literami α, β i γ.

Kąt centralny

Wcześniej wspominamy o kątu centralnym, wśród elementów zwykłego wielokąta, jest to kąt, którego wierzchołek znajduje się w środku wielokąta, a boki to segmenty, które łączą centrum z dwoma kolejnymi wierzchołkami.

Aby obliczyć miarę kąta centralnego α, 360º jest podzielone przez N, liczba stron. Lub 2π radian między N:

Może ci służyć: funkcja iniekcyjna: z czego składa się, do czego jest i przykłady

α = 360º/n

Równoważny w Radianach do:

α = 2π /n

Kąt wewnętrzny lub kąt wewnętrzny

Na rycinie 4 kąt wewnętrzny β jest tym, którego wierzchołek pokrywa. Jest obliczany w stopniach seksualnych przez:

β = [180 (n-2)]/n

Lub w radianach używających:

β = [π (n-2)]/n

Kąty zewnętrzne

Są one oznaczone grecką literą γ. Na rysunku obserwuje się, że γ + β = 180º. Dlatego:

γ = 180º - β

Suma wszystkich zewnętrznych kątów do zwykłego wielokąta wynosi 360º.

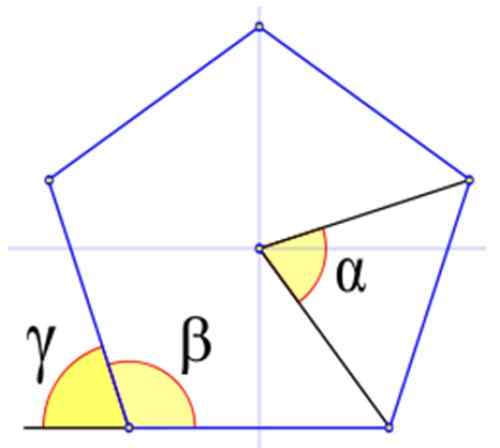Rysunek 4. Kąty w zwykłym wielokąta, w tym przykładzie regularny Pentagon. Źródło: Wikimedia Commons.

Przykłady zwykłych wielokątów

Poniżej mamy pierwsze 8 zwykłych wielokątów. Obserwujemy, że wraz ze wzrostem liczby stron wielokąt staje się coraz bardziej do obwodu, w którym są rejestrowane.

Możemy sobie wyobrazić, że długość boków coraz małe i zwiększając ich liczbę, otrzymujemy obwód.

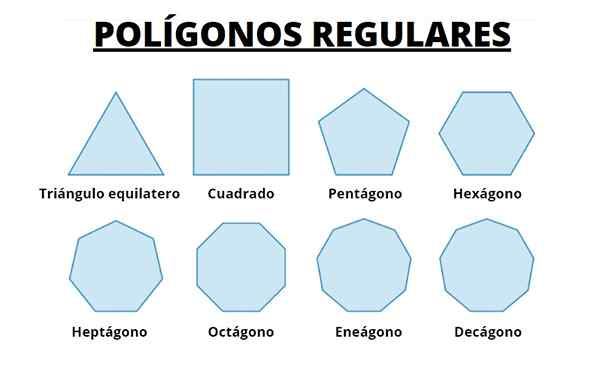Rysunek 5. Pierwsze osiem zwykłych wielokątów. Źródło: Wikimedia Commons.

- Regularne wielokąty w życiu codziennym i naturze

Regularne wielokąty znajdują się wszędzie w życiu codziennym, a nawet w naturze. Spójrzmy na kilka przykładów:

Sygnały drogowe

W oznakowaniu widzimy na autostradach i drogach obfitują w zwykłe wielokąty, takie jak trójkąty równoboczne, kwadratowe i rombowe. Na rycinie 6 widzimy sygnał sygnał o wysokiej w kształcie.

Rysunek 5.- Sygnał drogowy o ośmiokątnym kształcie. Źródło: Pixabay.

Meble

Niezliczone meble są na przykład kwadratowe, jako charakterystyczna postać geometryczna, a także wiele stołów, krzeseł i banków jest kwadratowych. Równoległobok jest na ogół pudełkiem z prostokątnymi stronami (co nie jest zwykłym wielokątem), ale mogą również sprawić, że kwadratowy.

Architektura i konstrukcja

Płytki lub płytki podłóg i ścian, zarówno w domach, jak i na ulicach, często mają formę zwykłych wielokątów.

TESELE to powierzchnie pokryte całkowicie płytkami, które mają różnorodne figurki geometryczne. Z trójkątem kwadrat i sześciokąt można wykonać zwykłe tesselvy, te, które używają tylko jednego rodzaju postaci do doskonale powlekania, bez pustych przestrzeni (patrz rysunek 6).

Również budynki wykorzystują regularne wielokąty w elementach takich jak okna i dekoracja.

Rysunek 6. Kwadratowy płytka. Źródło: Pixabay.

- Regularne heksagony w naturze

Zaskakujące jest to, że regularny sześciokąt jest wielokątem, który często pojawia się w naturze.

Może ci służyć: dyskretne dystrybucje

Plezy miodu wykonane przez pszczoły do ​​przechowywania miodu mają bardzo przybliżony kształt do zwykłego sześciokątla. Jak zauważył Pappus z Aleksandrii, w ten sposób pszczoły optymalizują przestrzeń, aby zaoszczędzić jak najwięcej miodu.

I są też regularne sześciokąt w skorupce żółwi i płatków śniegu, które również przyjmują różne bardzo piękne geometryczne kształty.

Ćwiczenie rozwiązane

Regularny sześciokąt jest częścią półkola o promieniu 6 cm, jak pokazano na rysunku. Jaka jest wartość zacienionego obszaru?

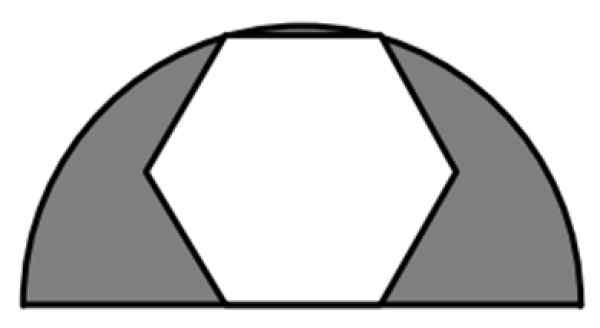Rysunek 7. Regularny sześciokąt zarejestrowany w półkole. Źródło: f. Zapata.

Rozwiązanie

Zacieniony obszar jest różnicą między obszarem półkola RADIUS r = 6 cm a pełnym obszarem sześciokątnym, regularnym wielokątem 6 -pasmowym. Będziemy potrzebować formuł dla obszaru każdej z tych figur.

Obszar półkola

DO₁ = π r² /2 = π (6 cm)² /2 = 18π cm²

Regularny obszar sześciokąta

Formuła obliczania obszaru zwykłego wielokąta jest:

A = p.A /2

Gdzie P To jest obwód i Do To jest apothem. Ponieważ obwód jest sumą boków, będziemy potrzebować ich wartości. Dla zwykłego sześciokąta:

P = 6ℓ

Dlatego:

A = 6ℓa /2

Aby znaleźć wartość strony ℓ Konieczne jest zbudowanie liczb pomocniczych, co wyjaśnimy poniżej:

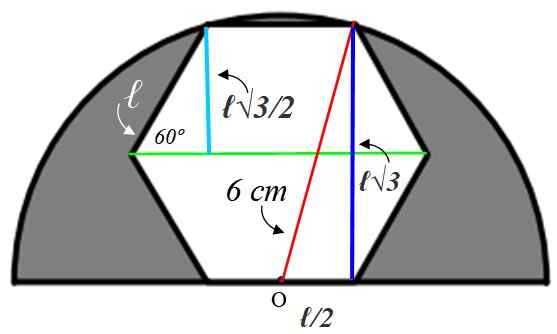
Zacznijmy od małego trójkąta prostokąta po lewej. Warto wewnętrzny kąt sześciokąta:

α = [180 (n-2)]/n = α = [180 (6-2)]/6 = 120º

Promień, który narysowaliśmy w kolorze Bisecta, ten kąt, dlatego ostrym kąt małego trójkąta wynosi 60º. Dzięki dostarczonym informacjom ten trójkąt jest rozwiązany, znajdując jasnoniebieską stronę, która mierzy tak samo jak Apothem:

Przeciwne cateto = a = ℓ x sin 60º = ℓ√3 / 2 cm

Ta wartość jest dwa razy więcej ciemnoniebieskiej nogi dużego trójkąta po prawej, ale z tego trójkąta wiemy, że przeciwprostanie mierzy 6 cm, ponieważ jest to promień półkola. Pozostałe Cateto (poniżej) jest warte ℓ/2 od punktu lub znajduje się na środku boku.

Ponieważ wewnętrzne kąty tego trójkąta nie są znane, możemy podnieść dla niego twierdzenie Pitagorasa:

36 = 3 ℓ² + ℓ² / 4

(13/4) ℓ² = 36 → ℓ = √ (4 x36) /13 cm = 12 /√13 cm

Z tą wartością oblicza się apothem:

a = ℓ√3 /2 cm = (12 /√13) x (√3 /2) cm = 6√3 /√13 cm

Zadzwońmy₂ do zwykłego obszaru sześciokątnego:

= 28. 8 cm²

Zacieniony obszar figur

DO₁ - DO₂ = 18π cm²  - 28.8 cm² = 27.7 cm²

Bibliografia

1. Baldor, a. 1973. Geometria i trygonometria. Redakcja kulturalna Ameryki Środkowej.
2. Ciesz się matematyką. Tesels. Odzyskane z: FaveMatimaticas.com.
3. I. DO. 2003. Elementy geometrii: z ćwiczeniami i geometrią kompasu. University of Medellin.
4. Heksagony w naturze. Odzyskany z: Malvargamath.WordPress.com.
5. Jiménez, r. 2010. Matematyka II. Geometria i trygonometria. Druga edycja. Prentice Hall.
6. Zwykłe wielokąty. Wyzdrowiał od: kolego.Inżynieria.USAC.Edu.Gt.
7. Wikipedia. Apothem. Odzyskane z: jest.Wikipedia.org.