kartezjański samolot

Jaki jest płaszczyzna kartezjański?

On kartezjański samolot Składa się z pary prostych linii prostopadłych do siebie i to przecinają się w jednym punkcie. Jedna z linii jest pionowa, a druga pozioma, przechodząc do punktu skrzyżowania jako pochodzenie systemu.

Celem jest łatwe zlokalizowanie dowolnego płaskiego punktu przez parę wartości: współrzędna. Aby to zrobić, w każdym z linii konstruowana jest skala z liczbami całkowitymi, pozytywne są zapisane w jednym kierunku, a negatywy w drugim, jak pokazano na poniższym rysunku:

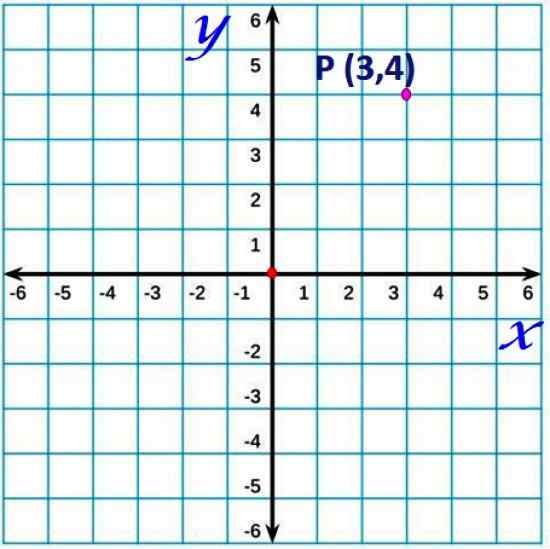
Rysunek 1. Punkt w płaszczyźnie kartezjańskim. Źródło: f. Zapata.

Zgodnie z konwencją osi pozioma jest zwykle nazywany osi x i pionową jako oś i.

Dowolny punkt samolotu będzie miał współrzędne określone przez parę uporządkowaną (X, y). Na przykład punkt P współrzędnej (3,4), zlokalizowany 3 jednostki po prawej stronie pochodzenia i 4 jednostki w górę, na górnej rysunku. Jest podobny do mapy, która wskazuje szerokość i długość określonej lokalizacji.

Ponieważ konieczne są dwa współrzędne, mówi się, że płaszczyzna jest dwukierunkowa, ale koncepcja jest łatwo rozszerzona na trzy wymiary, dodając bardziej współrzędną osi, która zwykle oznaczona jako oś Z. W takim przypadku współrzędne nabierają kształtu (X i z).

Samolot kartezjański otrzymuje swoją nazwę od francuskiego naukowca René Descartes (1596-1650), który sformalizował ją w swojej pracy Metoda mowa z 1637 r., Chociaż w pracach Apolloniusza z Pergi (262-190 AC), matematyka, który odkrył stożkowe krzywe: obwód, elipsa, przypowieść i hiperbola.

Może ci służyć: Kubki Różnica: wzory, równania, przykłady, ćwiczenia

Charakterystyka płaszczyzny kartezjańskiej

- Jak on Oś x Jak Oś y Rozciągają się nieskończenie na obu końcach i przecinają się prostopadle (pod kątem 90 stopni). Ta funkcja nazywa się ortogonalność.

- Punkt, w którym przecinają się obie osie, jest znany jako pochodzenie lub punkt zerowy.

- Układ współrzędnych dzieli płaszczyznę na cztery regiony zwane kwadrantami.

- Lokalizacje w płaszczyźnie współrzędnych są opisane jako pary uporządkowane.

- Każdy punkt na płaszczyźnie kartezjański jest powiązany z unikalną współrzędną X i współrzędną i unikalną.

Elementy płaszczyzny kartezjańskiej

Elementy płaszczyzny kartezjańskiej są następujące:

- Linie numeryczne albo współrzędne osie X i y, Jeśli to samolot. Oś I odbieraj nazwę osi rzędnych, podczas gdy oś osi X Jest to oś odciętej. Jeśli chodzi o przestrzeń, dodaje się oś z, w stanie przedstawić zarówno wysokość, jak i głębokość.

-On pochodzenie, który jest punktem przecięcia osi.

- ćwiartki, które są regionami, które osie współrzędnych określają w płaszczyźnie i są liczone w przeciwnym kierunku do dłoni zegara, zaczynając od pierwszego kwadrantu. Są one zdefiniowane w następujący sposób:

• Pierwszy kwadrant: osie X I I pozytywny.
• Drugi kwadrant: odpowiadający ujemnej osi x i osi dodatniej.
• Trzeci kwadrant: ma oba osie ujemne.
• Czwarty kwadrant: z dodatnią osą x i osą ujemną.

Zasadniczo ćwiartki są oznaczone w liczbach rzymskich, tak jak to:

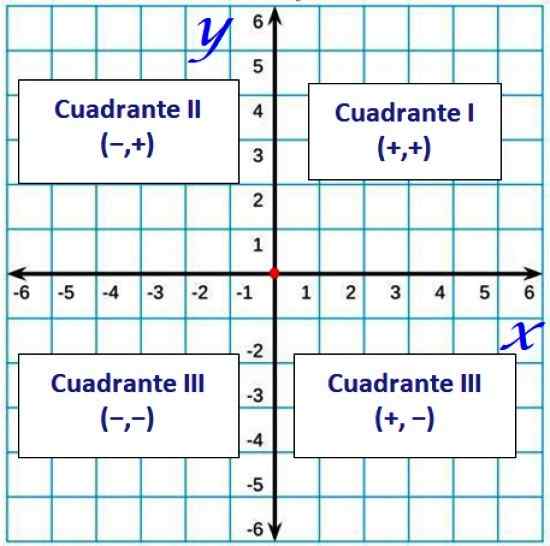Rysunek 2. Cuadrants w płaszczyźnie kartezjańskim. Źródło: f. Zapata.

Zamówione pary i odległość między dwoma punktami

Uporządkowane pary to współrzędne każdego punktu, w którym współrzędna X jest zawsze umieszczona na pierwszym miejscu, jak na przykładzie rysunku 1. Współrzędne (3,4) punktu p wskazują, że x = 3 I y = 4.

Na drugim rysunku poniżej punkt P należy do kwadrantu dożylnego i ma współrzędne (2; −1.5). Zauważ, że wystając linie od osi współrzędnych do punktu P tworzy prostokąt. To jest powód, dla którego nazywane są również współrzędne kartezjańskie Prostokątne współrzędne.

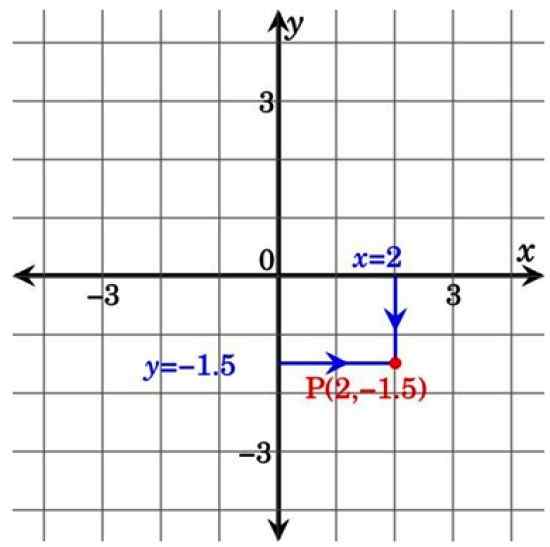Rysunek 3. Punkt na płaszczyźnie kartezjańskiej. Źródło: Wikimedia Commons.

Zastosowania samolotów kartezjańskich

Samolot kartezjański ma wiele zastosowań w wielu dziedzinach. Początkowo Kartezjusz wprowadził go do wykresu krzywych krzywych w płaszczyźnie, dlatego jest uważany za ojca geometrii analitycznej.

Może ci służyć: produkt Cruz

Jednak jego użycie rozciąga się na wykres wszelkiego rodzaju relacji i funkcji, takich jak:

-Podążaj za trajektorią ciała o ruchu parabolicznym, okrągłym lub krzywoliniowym w ogóle.

-Graficznie określ sposób, w jaki dwie zmienne są powiązane za pomocą funkcji.

-Znajdź punkty na płaskiej ziemi, aby ułatwić im pomiary.

Bibliografia

1. Matematyka jest zabawna. Współrzędne kartezjańskie. Odzyskany z: MathSisfun.com/data/cartezian współrzędne.
2. Samolot kartezjański. Źródło: DL.Uncw.Edu.