Obliczenia wagowe (fizyczne), jednostki, przykłady, ćwiczenia

On waga Jest to siła, z którą Ziemia przyciąga przedmioty na swoją powierzchnię. Za każdym razem, gdy obiekt jest upuszczony, idzie na ziemię, nie jest w stanie wspinać się na własne środki, ani nie jest niezmieniony w połowie drogi, co oznacza, że ​​ziemia go przyciąga.

Wszystkie obiekty niezmiennie przyciągają ze sobą, nawet najmłodsze, tylko że wielkość siły, z którą robią, jest proporcjonalna do masy. Oznacza to, że obiekty o niewielkiej masie wywierają niewielką siłę na inne, ale ciała niebieskie, takie jak Ziemia, są w stanie wywierać bardzo dużą siłę.

Ziemia utrzymuje wokół niej księżyc dzięki tej sile przyciągania, który się nazywa Przyciąganie grawitacyjne Jeśli chodzi o obiekty, które są dalekie od powierzchni ziemi i waga Kiedy obiekty są blisko.

Wynika to z tego, że siła grawitacji nie wymaga, aby obiekty niekoniecznie kontaktują się ze sobą: dlatego mówi się, że jest to siła działania na odległość.

Obiekty nadal mają wagę, nawet jeśli znajdują się na pewnej wysokości na ziemi i im bardziej masywne, tym większa będzie ta waga.

Wielki angielski naukowiec Isaac Newton jako pierwszy przedstawił wyjaśnienie tego problemu, poprzez powszechne prawo grawitacyjne, które nosi jego imię i od tego czasu służyło zrozumieniu, w jaki sposób obiekty oddziałują na masę z masą. Jest to bardzo ważne, ponieważ każdy obiekt na planecie ma wagę.

[TOC]

Jednostki wagowe

System jednostek międzynarodowych, jeśli waga jest waga Niuton, Nazwany na cześć Izaaka Newtona. Jest to jednostka do pomiaru wszelkiego rodzaju sił.

Newton, skrócony N, jest zdefiniowany jako niezbędna siła dla obiektu masowego 1 kg do uzyskania przyspieszenia 1m/s². Oprócz Newtona istnieją inne jednostki siły powszechnego użytkowania, na przykład:

Siła kilograma

On siła kilograma o Kilopondio, skrócony KG-F lub KP, choć powszechnie nazywany Kg bez dalszych. Konieczne jest określenie lokalizacji, ponieważ, jak wspomniano, pole grawitacyjne doświadcza wariantów o wysokości i szerokości geograficznej.

Kiedy ktoś mówi, że waży 45 kg, w rzeczywistości oznacza to, że ich waga wynosi 45 kg-f, ponieważ kilogram jest jednostką zarezerwowaną dla masy.

Może ci służyć: Otwarty obwód

Równoważność między kg-f i n wynosi: 1 kg-f = 9.8 n

Siła funta

Libra-fuerza, Skrócony LB-F jest również jednostką siły, która jest analogiczna do KG-F, ponieważ jest to siła, którą Ziemia wywiera na obiekt 1 funta masy. I podobnie jak w przypadku KG-F, nie ma problemu z wartościami, gdy jesteś na ziemi, to znaczy obiekt masy, waży 1 lb-f-f.

Równoważność w LB-F i N wynosi: 1 funt-f ≡ 4.44822 n.

Obliczanie masy i wzór

Waga obiektu jest proporcjonalna do jego masy. Większa masa, większa waga.

Wzór do znalezienia wielkości masy p (lub w, jak czasami oznacza, przez "Waga" W języku angielskim) jest to bardzo proste:

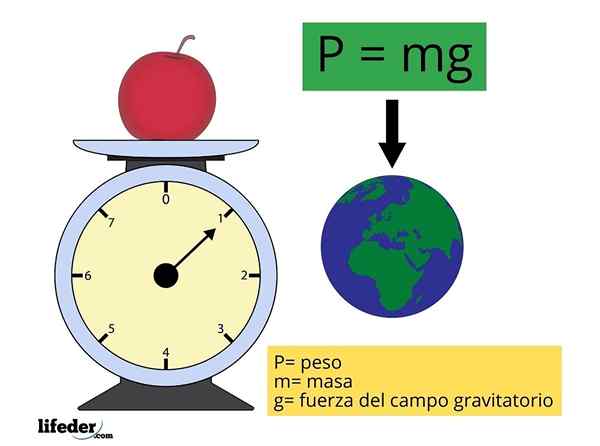
P = mg

Gdzie M reprezentuje masę obiektu i G Jest to wielkość przyspieszenia grawitacji (intensywność pola grawitacyjnego lub nasilenia), w przybliżeniu stała i której wartość jest przyjmowana jako 9.81 m/s² Dla najczęstszych obliczeń.

Waga jest wektorem i rozróżnianie wektora od jego wielkości stosowane są odważne litery. W ten sposób, gdy mówił o p, rozumie się, że jest to wartość liczbowa i kiedy jest napisana P Odniesienie do wektora:

P = m ∙G

 G Z odważnymi tekstami jest to pole grawitacyjne lądu, to znaczy wpływ, jaki ziemia wywiera na otaczającą ją przestrzeń, niezależnie od tego, czy istnieje inne ciało, które go dostrzega. Każdy obiekt o masie ma własne pole grawitacyjne, zarówno małe, jak i duże.

Intensywność pola grawitacyjnego lądu G To nie jest całkowicie stałe. Ma niewielkie odmiany, które powstają głównie dlatego, że Ziemia nie jest idealną kulą, a także do lokalnych różnic wysokości i gęstości. Ale w przypadku większości aplikacji wartość 9.81 m/s² Pracuje bardzo dobrze.

Inne ciała niebieskie mają swoje własne charakterystyczne pole grawitacyjne, dlatego przyspieszenie grawitacji różni się w zależności od planety lub satelity. Ten sam obiekt miałby inną wagę w każdym z nich, stąd waga nie jest charakterystyczną właściwością rzeczy, ale ogólnie podmiotu.

Waga jako wektor

Waga jest wektorem i dlatego ma wielkość, kierunek i znaczenie. W pobliżu powierzchni Ziemi ciężar jest wektorem pionowym, a kierunek jest zawsze w dół.

Ogólnie rzecz biorąc, adres pionowy jest mianowany osi I albo z, A znaczenie przypisuje się znak + lub znak - w celu odróżnienia go od kierunku w górę. Wybór zależy od lokalizacji pochodzenia. Na niższym obrazie pochodzenie zostało wybrane w punkcie, z którego opadają Apple:

Może ci służyć: idealny gaz: model, zachowanie, przykłady Waga to wektor, który jest skierowany pionowo. Źródło: f. Zapata.

Wektor jednostki J, Wektor wielkości równy 1, służy do wskazywania i rozróżnienia kierunku pionowego. Jeśli chodzi o ten wektor, waga jest napisana w ten sposób:

P = mg ( - J)

Gdzie znak ujemny jest przypisany do kierunku.

Różnice między wagą, masą i objętością

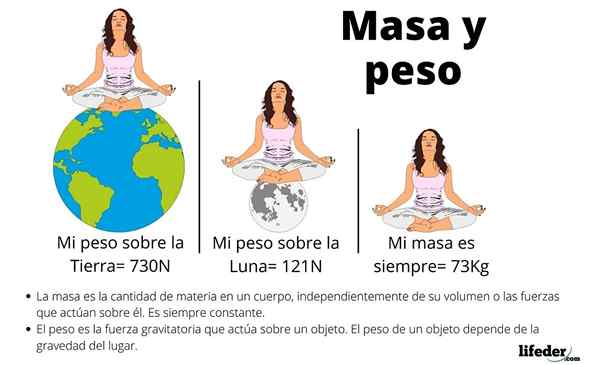
Często te trzy koncepcje są zdezorientowane, ale przeglądając cechy wagi, łatwo jest go odróżnić od masy i objętości.

Na początek waga zależy od pola grawitacyjnego miejsca, w którym znajduje się obiekt. Na przykład na ziemi i na księżycu ta sama rzecz ma inną wagę, chociaż ilość atomów, które się tworzą.

Masa jest wielkością skalarną, związaną z ilością atomów, które składają się na obiekt i jest dowodzona oporem, że obiekt musi zmienić ruch, nazywana właściwość nazywana bezwładność.

Ze swojej części objętość jest miarą przestrzeni zajmowanej przez obiekt, kolejną ilość skalarnego. Dwa obiekty o równej objętości nie ważą tak samo, na przykład żelazna kostka waży znacznie więcej niż inny polistyren o tych samych wymiarach.

W podsumowaniu:

• Masa jest związana z ilością materii, którą ma ciało.
• Waga to siła wywierana przez ziemię na tę masę, proporcjonalną do niej.
• Tom to przestrzeń zajmowana przez materię.

Należy zauważyć, że będąc wielkościami skalarnymi, ani masa, ani objętość nie mają kierunku, ani znaczenia, ale tylko wartość liczbowa i odpowiednia jednostka. Z drugiej strony waga, będąc wektorem, musi być zawsze poprawnie wyrażona wskazując wielkość, jedność, kierunek i znaczenie, jak w poprzednim rozdziale.

Przykłady wagi

Wszystkie obiekty na ziemi mają wagę, możesz nawet „ważyć” obiekty, które nie są na ziemi, takie jak inne planety lub słońce, chociaż w środkach pośredniego, oczywiście tak jest.

Ponieważ zasięg wagi jest bardzo duży, stosuje się notację naukową (w mocy 10), aby wyrazić niektóre, które są bardzo duże lub bardzo małe:

-The Sun: 1989 × 10³⁰ Kg-f

-Jowisz: 1 898 × ​​10²⁷ Kg-f

-Komar: 2.0 × 10^-5 N

-Niemowlęta: 34.3 n

-Dziecko: 353 n

-Osoba dorosła: 65 kg-f

-Słoń dorosły: 5.5 × 10³ Kg-f

-Blue Whale: 1.0 × 10⁶ N

Ćwiczenie rozwiązane

Ciasto 20 kg spoczywa na stole.

a) Znajdź wagę pudełka i normalną siłę, którą wywiera na nią stół.

Może ci służyć: ochrona pędu liniowego: zasada, przykłady, ćwiczenia.

b) Kolejne 10 kg pudełka jest umieszczone na pierwszym. Znajdź normalny, który stół ćwiczy na polu 20 kg i normalnym, który wywiera na najmniejszym pudełku.

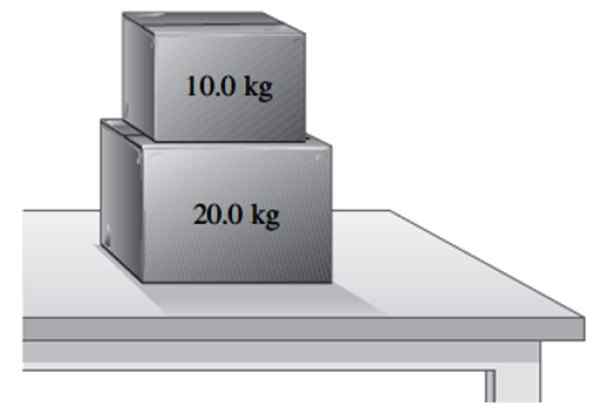Dwa pudełka spoczywające na stole. Źródło: f. Zapata.

Rozwiązanie

Wygodne jest wykonanie bezpłatnego schematu ciała na pudełku, który polega na rysowaniu na nim sił.

W tej sytuacji wciąż jest najmniejsze pudełko na górze, dlatego są tylko dwie siły: pierwsze to waga P który jest rysowany pionowo, jak wskazano w poprzednich sekcjach, a następnie jest normalne N, która jest siłą prostopadłą, którą stół wywiera i zapobiega upadku pudełka.

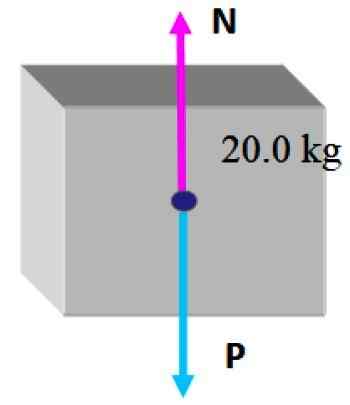
Ponieważ pudełko jest w równowadze statycznej w tych okolicznościach, rozsądne jest stwierdzenie, że wielkość normalnego jest taka sama jak waga, aby mogła zatem zrekompensować:

N = mg = 20.0 kg x 9.8 m/s² = 196 N; skierowane pionowo.

Ze swojej strony waga wynosi p = 196 n ukierunkowana pionowo.

Rozwiązanie b

Teraz powstają nowe bezpłatne schematy ciała o obu przedmiotach. W przypadku dużego pudełka nieco się zmieniają, ponieważ małe pudełko wywiera na to siłę.

Siły są następujące: N I P Są odpowiednio normalne, które ćwiczy stół i ciężar na pudełku po 20.0 kg, to się nie zmieniło. A nowa siła wywierana przez małe pudełko jest N₁, normalna z powodu kontaktu z górną powierzchnią dużego pudełka.

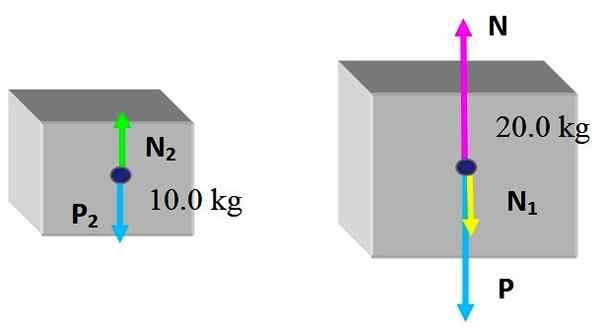
Jeśli chodzi o małe pudełko, otrzymuje normę N₂, wywierane przez górną twarz dużego pudełka i oczywiście jego wagę P₂. Ponieważ pudełka są równowagą statyczną:

N₂ - P₂ = 0

N - n₁ - P = 0

Od pierwszego równania musisz n₂ = P₂ = 10 kg x 9.8 m/s² = 98 n. Zgodnie z prawem działania i reakcji wielkość siły, którą otrzymuje małe skrzynkę, jest tym samym, co wywiera na duże pudełko, zatem:

N₂ = N₁ = 98 n

Z drugiego równania normy N, że stół ćwiczy na dużym pudełku, jest wyczyszczone, które z kolei ma małe pudełko na górze:

N = n₁ + P = 98 N + 196 n = 294 n

Bibliografia

1. Figueroa, zm. 2005. Seria: Fizyka nauk i inżynierii. Głośność 2. Dynamiczny. Pod redakcją Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fizyka. 2. Wyd. McGraw Hill.
3. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6th. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1. osoba.
5. Serway, r., Jewett, J. 2008. Fizyka nauk i inżynierii. Tom 1. 7th. Wyd. Cengage Learning.
6. Thomas Griffith, w. 2007. Fizyka koncepcyjna. MC Graw Hill.