Y = 3Sen (4x) Okres funkcji

On Y = 3Sen (4x) Okres funkcji To 2π/4 = π/2. Aby jasno zrozumieć przyczynę tego stwierdzenia, musi być znana definicja okresu funkcji i okresu funkcji Sen (x); Przydanie się również trochę o funkcji.

Funkcje trygonometryczne, takie jak zatokę i cosinus (Sen (X) i cos (x)), są bardzo przydatne zarówno w matematyce, jak i inżynierii.

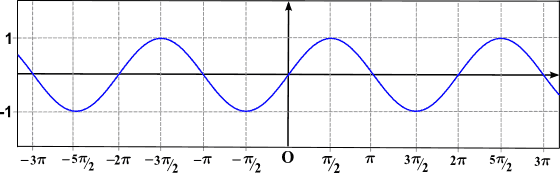
Okres słowa wspomina o powtórzeniu zdarzenia, więc stwierdzenie, że funkcja jest okresowa, jest równoważne powiedzenie „jej wykres jest powtórzeniem kawałka krzywej”. Jak widać na poprzednim obrazie, funkcja SEN (x) jest okresowa.

Funkcje okresowe

Mówi się, że funkcja f (x) jest okresowa, jeśli istnieje wartość rzeczywistą p ≠ 0, tak że f (x+p) = f (x) dla wszystkich x w dziedzinie funkcji. W takim przypadku okres funkcji to p.

Jest ogólnie nazywany okresem funkcji przy najniższej pozytywnej liczbie rzeczywistej p, która spełnia definicję.

Jak widać na poprzednim wykresie, funkcja Sen (x) jest okresowa, a jej okres wynosi 2π (funkcja cosinus jest również okresowa, z okresem równym 2π).

Zmiany na wykresie funkcji

Niech f (x) będzie funkcją, której wykres jest znany i będzie stałą dodatnią. Co dzieje się z wykresem f (x), jeśli mnoży f (x) przez c? Innymi słowy, jak jest wykres C*f (x) i f (cx)?

C*F Wykres (x)

Poprzez pomnożenie funkcji, zewnętrznie, przez stałą dodatnią, wykres f (x) ulega zmianie wartości wyjściowych; Oznacza to, że zmiana jest pionowo i można podjąć dwa przypadki:

- Jeśli C> 1, wykres cierpi na pionowy odcinek z współczynnikiem C.

- Tak 0

F Wykres (CX)

Gdy argument funkcji jest mnożony przez stałą, wykres f (x) cierpi na zmianę wartości wejściowych; Oznacza to, że zmiana jest pozioma i, jak wcześniej, można podjąć dwa przypadki:

- Jeśli C> 1, wówczas wykres cierpi na kompresję poziomą o współczynniku 1/c.

- Tak 0

Y = 3Sen (4x) Okres funkcji

Należy zauważyć, że w funkcji f (x) = 3se (4x) istnieją dwie stałe, które zmieniają wykres funkcji zatok: jeden mnożący zewnętrzny, a drugi w sposób wewnętrzny.

3, który jest poza funkcją sinuso. Oznacza to, że wykres funkcji 3Sen (x) będzie między wartościami -3 i 3.

4, które znajduje się w funkcji sinuso.

Z drugiej strony okres funkcji jest mierzony poziomo. Ponieważ okres funkcji Sen (x) wynosi 2π, biorąc pod uwagę SIN (4x), wielkość okresu się zmieni.

Wiedzieć, jaki jest okres y = 3sen (4x), po prostu pomnożić okres funkcji Sen (x) przez 1/4 (współczynnik kompresji).

Innymi słowy, okres funkcji y = 3sen (4x) wynosi 2π/4 = π/2, co można zobaczyć na ostatniej grafice.