Obwód koła, jak go wydostać i formuły, rozwiązane ćwiczenia

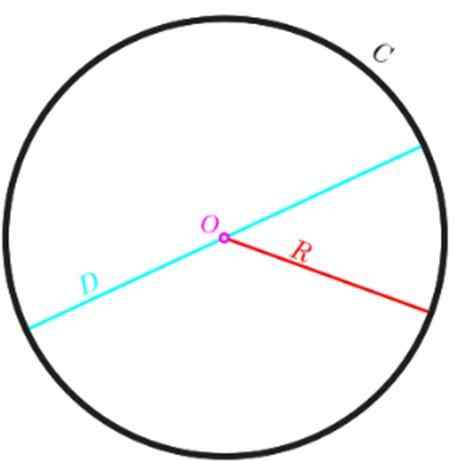
On obwód koła Jest to zestaw punktów, które tworzą kontur koła i jest również znany jako długość obwodu. Zależy to od promienia, ponieważ większy obwód oczywiście będzie miał większy kontur.

Być P Obwód koła i R promień tego samego, wówczas możemy obliczyć P Z następującym równaniem:

P = 2π.R

Obwód koła (w tym przypadku pizza) zależy od jego radia. Źródło: Pixabay.

Gdzie π jest liczbą rzeczywistą (czyta „pi”), która jest warta około 3.1416… punkty zawiesinowe są spowodowane faktem, że π ma nieskończone dziesiętne dziesiętne. Dlatego przy dokonywaniu obliczeń konieczne jest zaokrąglanie jej wartości.

Jednak w przypadku większości aplikacji wystarczy przyjąć wskazaną tutaj kwotę lub użyć wszystkich dziesiętnych, z którymi działa kalkulator.

Jeśli zamiast promienia, preferuje się użycie średnicy D, co wiemy, że jest dwa razy większy niż promień, obwód jest wyrażany w następujący sposób:

P = π.2R = π.D

Ponieważ obwód ma długość, zawsze należy go wyrażać w jednostkach takich jak mierniki, centymetry, stopy, cale i więcej, w zależności od preferowanego systemu.

[TOC]

Obwody i koła

Często są używane terminy zamiennie, to znaczy jako synonimy. Ale zdarza się, że istnieją między nimi różnice.

Słowo „obwód” pochodzi z greckiego „okresu”, co oznacza kontur i „metra” lub miarę. Obwód jest konturem lub obwodem koła. Formalnie jest zdefiniowany:

Obwód jest zestawem punktów o równej odległości od punktu zwanego środkiem, a odległość ta jest promieniem obwodu.

Ze swojej strony okrąg jest zdefiniowany w następujący sposób:

Okrąg to zestaw punktów, którego odległość do punktu zwanego środkiem jest mniejsza lub równa stałej odległości zwanej radio.

Czytelnik może ostrzec subtelną różnicę między obiema pojęciami. Obwód odnosi się tylko do zestawu punktów krawędzi, podczas gdy okrąg jest zestawem punktów od krawędzi do wewnątrz, którego obwód jest granicą.

Może ci służyć: ćwiczenia prześwitu formuły

Ćwiczenia DEmostracja obliczeń obwodu koła

Dzięki następującym ćwiczeniom opisane pojęcia zostaną wprowadzone w życie, a także niektóre inne, które zostaną wyjaśnione, gdy się pojawią. Zaczniemy od najprostszych, a stopień trudności wzrośnie stopniowo.

- Ćwiczenie 1

Znajdź obwód i obszar koła radiowego 5 cm.

Rozwiązanie

Równanie podane na początku jest stosowane bezpośrednio:

P = 2π.R= 2π.5 cm = 10 π cm = 31.416 cm

Aby obliczyć obszar DO Zastosowana jest następująca formuła:

DO = π.R² = π. (5 cm)²= 25π cm²= 78.534 cm²

- Ćwiczenie 2

a) Znajdź obwód i obszar pustego regionu z poniższej liczby. Środek zacienionego okręgu znajduje się w czerwonym punkcie, a środek białego obwodu jest zielonym punktem.

b) Powtórz poprzedni rozdział dla zacienionego regionu.

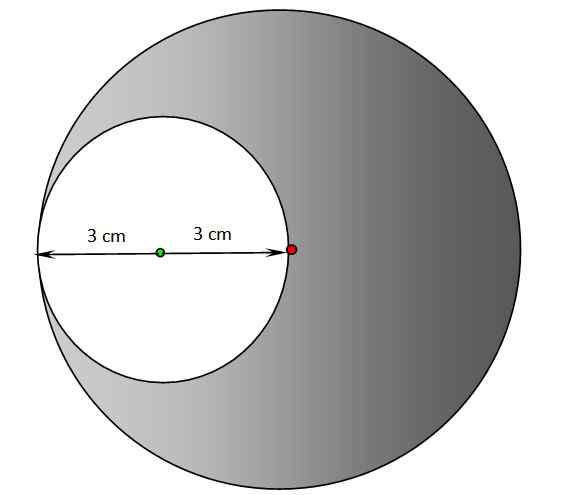Kręgi do ćwiczeń 2. Źródło: f. Zapata.

Rozwiązanie

a) Promień obwodu białego wynosi 3 cm, dlatego stosujemy te same równania, co w ćwiczeniu 1:

P = 2π.R= 2π.3 cm = 6 π cm = 18.85 cm

DO = π.R² = π. (3 cm)²= 9π cm²= 28.27 cm²

b) W przypadku zacienionego okręgu promień wynosi 6 cm, jego obwód jest dwa razy większy niż jeden obliczony w sekcji A):

P = 2π.R= 2π.6 cm = 12 π cm = 37.70 cm

I wreszcie obszar zacienionego regionu jest obliczany w następujący sposób:

- Pierwszy to obszar zacienionego koła, jakby był kompletny, który nazwiemy ”, tak:

DO' = π.R²= π.(6 cm)² = 36π cm²= 113.10 cm²

- Następnie w okolicy DO' Obszar białego okręgu jest odejmowany, wcześniej obliczany w sekcji A), w ten sposób uzyskiwany jest żądany obszar, który zostanie oznaczony po prostu jako:

A = a ' - 28.27 cm² = 113.10-28.27 cm² = 84.83 cm²

- Ćwiczenie 3

Znajdź obszar i obwód zacienionego regionu na poniższym rysunku:

Może ci służyć: kąty uzupełniające: co to są, obliczenia, przykłady, ćwiczenia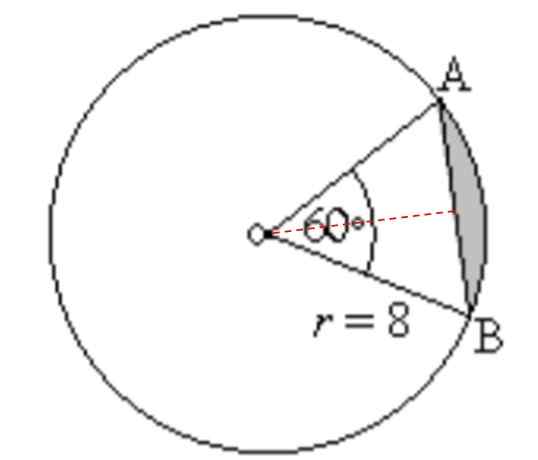Rysunek do ćwiczenia 3. Źródło: f. Zapata.

Rozwiązanie

Obliczenie obszaru zacienionego regionu

Najpierw obliczamy obszar Sektor okrągły lub klin, między segmentami prostymi OA i OB oraz okrągłym segmentem AB, jak pokazano na poniższym rysunku:

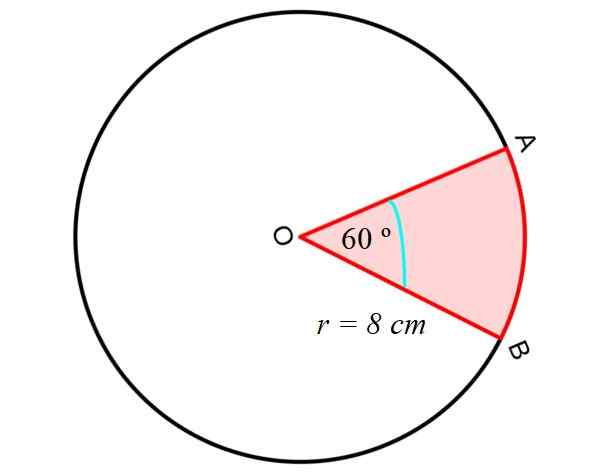
W tym celu stosuje się następujące równanie, które daje nam obszar sektora okrągłego, znając promień R i kąt środkowy między segmentami OA i OB, to znaczy dwa radia obwodu:

DO _{Sektor okrągły} = Π.R². (αº/360º)

Gdzie αº jest kątem centralnym - jest centralny, ponieważ jego wierzchołek jest środkiem obwodu - między dwoma radia.

Krok 1: Obliczanie powierzchni sektora okrągłego

W ten sposób obszar sektora pokazany na rysunku jest:

DO _{Sektor okrągły} = Π.R². (αº/360º) = π. (8 cm)². (60º/360º) = (64/6) π cm²= 33.51 cm²

Krok 2: Obliczanie obszaru trójkąta

Następnie obliczymy obszar białego trójkąta na ryc. 3. Ten trójkąt jest równoboczny, a jego obszar to:

DO _trójkąt = (1/2) Wysokość podstawy x

Wysokość jest kropkowana czerwona linia widoczna na rycinie 4. Aby go znaleźć, możesz na przykład użyć twierdzenia Pitagorasa. Ale to nie jedyny sposób.

Czytelnik obserwatora zauważy, że trójkąt równoboczny jest podzielony na dwa identyczne prostokąty, których podstawa wynosi 4 cm:

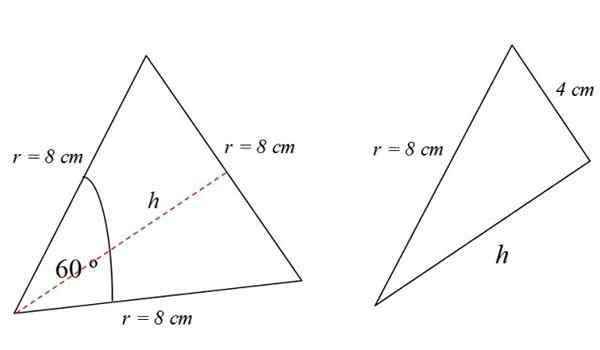
W prawym trójkącie twierdzenie Pitagorasa jest spełnione, dlatego:

Ponieważ masz wysokość trójkąta, zarówno prostokąta, jak i równoboczny, jego powierzchnia jest obliczana:

DO _trójkąt = (1/2) Podstawa x wysokość = (1/2) 8 cm x 6.93 cm = 27.71 cm².

Krok 3: Obliczanie zacienionego obszaru

Wystarczy odjąć główny obszar (obszar sektora okrągłego) mniejszego obszaru (obszarem trójkąta równobocznego): a _{zacieniony region} = 33.51 cm² - 27.71 cm² = 5.80 cm².

Obliczanie obwodu zacienionego regionu

Wyszukiwany obwód jest sumą strony prostoliniowej 8 cm i łuku obwodu AB.  Jednak całkowity obwód stwierdza 360 °, zatem łuk, który podpisuje 60 °, jest szóstą częścią pełnej długości, która, jak wiemy, to 2.π.A:

Może ci służyć: Funkcja rosnąca: jak to zidentyfikować, przykłady, ćwiczenia

AB = 2.π.R / 6 = 2.π.8 cm / 6 = 8.38 cm

Zastępując, obwód zacienionego regionu to:

P = 8 cm + 8.38 cm = 16.38 cm.

Aplikacje

Obwód, podobnie jak obszar, jest bardzo ważną koncepcją geometrii i wielu zastosowań w życiu codziennym.

Artyści, projektanci, architekci, inżynierowie i wiele innych osób korzystają z obwodu, jednocześnie rozwijając swoją pracę, zwłaszcza koło, ponieważ okrągły kształt jest wszędzie: od reklamy, przez jedzenie po maszyny.

Obwód i okrąg należą do najczęściej używanych geometrii. Źródło: Pixabay.

Aby wiedzieć bezpośrednio długość koła, wystarczy owinąć go nicią lub sznurkiem, a następnie rozszerzyć tę gwint i zmierzyć taśmą taśmową. Drugą alternatywą jest pomiar promienia lub średnicy koła i użycie niektórych formuł opisanych powyżej.

W codziennej pracy koncepcja obwodu jest używana, gdy:

-Odpowiednia pleśń jest wybierana dla określonej pizzy lub ciasta.

-Zostanie zaprojektowana droga miejska poprzez obliczenie wielkości pierścieni, w której samochody mogą zwrócić się do zmiany znaczenia.

-Wiemy, że Ziemia kręci się wokół Słońca w przybliżeniu okrągłej orbity -w rzeczywistości planetarne orbity są eliptyczne, zgodnie z prawami Keplera -ale obwód jest bardzo dobrym podejściem do większości planet.

-Wybrany jest odpowiedni rozmiar pierścienia lub pierścienia, który zostanie zakupiony w sklepie internetowym.

-Wybieramy klucz do odpowiedniego rozmiaru, aby poluzować nakrętkę.

I wiele więcej.

https: // youtu.Be/cr8xjryl5tk

Bibliografia

1. Bezpłatne samouczki matematyczne. Obszar i obwód kalkulatora okręgu - geometrii. Odzyskane z: Analezemath.com.
2. Odniesienie do otwartego matematyki. Obwód, obwód koła. Odzyskane z: Mathpenref.com.
3. Monterey Institute. Obwód i obszar. Odzyskane z: Montereyinstitute.org.
4. Naukowe. Jak znaleźć obwód koła. Odzyskane z: naukowe.com.
5. Wikipedia. Obwód. Źródło: w:.Wikipedia.org.