Elementy pentadecágono, klasyfikacja, cechy, ćwiczenia

A Pentadecantagon Jest to płaska postać zbudowana z piętnastoma prostymi segmentami i zamknięta. Tego rodzaju postacie są nazywane wielokąt i są nazwani zgodnie z liczbą stron, które mają.

Trójkąt, z trzema stronami i czworobokiem, są przykładami bardzo znanych wielokątów, ale wielokąty mogą mieć więcej stron.

Rysunek 1.  Zwykły Pentagon z czerwonymi wierzchołkami. Źródło: Wikimedia Commons.

Podstawowe elementy pentadecágono są takie same jak każdy wielokąt, niezależnie od ilości posiadanych stron. Te elementy to:

-boki, które są segmentami, które składają się na pentadecágono za łącznie 15.

-Wierzchołki, także 15, które są końcami sąsiednich stron.

-Kąty wewnętrzne, Te, które powstają w pentadecágono między dwiema sąsiednimi stronami.

-Kąty zewnętrzne, utworzone między jedną stroną a przedłużeniem jednej z kolejnych stron.

-Piagonals, Segmenty linii, które łączą dwa nie -adjacen wierzchołki.

[TOC]

Klasyfikacja

Pentadecágono może być regularny albo nieregularny, w zależności od wielkości ich boków i miary jego wewnętrznych kątów. Jeśli masz wszystkie boki i równe kąty wewnętrzne - Quilátero i równomierne - jest to regularne, jak pokazano na rycinie 1, w przeciwnym razie jest nieregularny.

Można go również zaklasyfikować jako wypukły albo wklęsły. Wklęsły Pentagon ma jeden lub więcej kątów wewnętrznych większych niż 180º, podczas gdy jeden zawsze wypukły ma wewnętrzne kąty mniejsze niż 180º. Zwykły Pentagon to wypukły.

Kolejne kryteria klasyfikacji są rozważane, jeśli jego strony nieobserwowe - lub ich rozszerzenia - są cięte lub nie. Kiedy nie są cięte, jak na rycinie 1, mówi się, że jest to prosty pentadecágon. A jeśli zostaną wycięte, to jest złożone.

Może ci służyć: geometria analityczna

Zwykły Pentagon

Regularny Pentagon, którego boki i kąty wewnętrzne mają tę samą miarę, jest liczbą wielkiej symetrii, ponieważ następujące dodatkowe elementy są zdefiniowane dla wcześniej opisanych:

-Centrum: Punkt, w którym równoznacz wierzchołki i boki.

-Radio: Odległość od środka do jednego ze zwykłych wierzchołków pięciokątnych.

-Kąt centralny: Ten, który ma wierzchołek na środku figury, a jej boki przechodzi przez dwa sąsiednie wierzchołki.

-Apothem, To segment prostopadły łączy się na środek jednej strony ze środkiem figury.

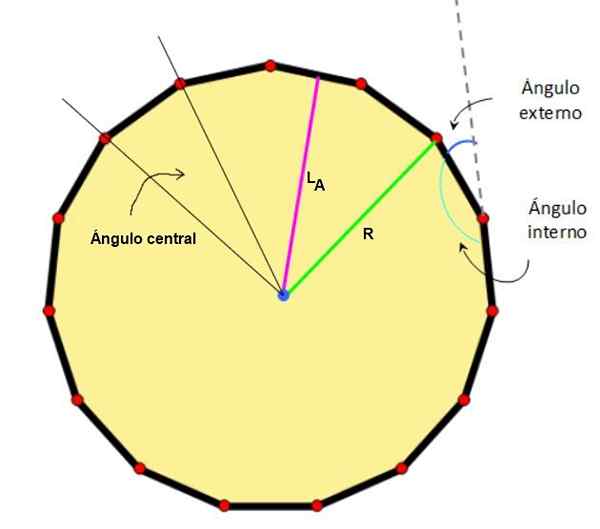Rysunek 2. Centrum, Apothem, radio i znaczące kąty pentadecágono. Źródło: Wikimedia Commons/F. Zapata.

- Charakterystyka zwykłego Pentagonu

Kąty wewnętrzne

Do obliczenia pomiaru I wewnętrznych kątów dowolnego zwykłego wielokąta, gdzie N Jest to liczba stron:

W tym wzorze, miara I jest w stopniach, aby wyrazić ją w radianach, jest ona mnożona przez współczynnik π/180. Zobaczmy, jaka jest miara wewnętrznych kątów zwykłego Pentagonu, zastępując n = 15:

I = [(15-2) × 180º]/15 = 156º

Równoważne 13π/15 radian. Ponieważ wewnętrzne kąty zwykłego pięciokąta są mniejsze niż 180º, jest to wypukły wielokąt.

Suma kątów wewnętrznych

Możliwe jest obliczenie sumy wewnętrznych kątów za pomocą następującego wzoru:

S = (n-2) x 180º

Jak zawsze N ​​reprezentuje liczbę stron. Ta formuła jest ważna dla n = 3, 4, 5 .. .

Dokonanie n = 15 otrzymujemy:

S = (15–2) x 180º = 2340º

Kąty zewnętrzne

Kąt wewnętrzny i kąt zewnętrzny są uzupełniające, to znaczy jego suma wynosi 180º, jak zauważono na rycinie 2. Dlatego zewnętrzny kąt Pentadecágono mierzy:

Może ci służyć: sprzężony dwumian: jak jest rozwiązany, przykłady, ćwiczenia

180 ° - 156º = 24º.

Obwód i obszar

Obwód jest miarą konturu wielokąta i łatwo dodaje wszystkie strony. Tak Do Jest to długość boku, wystarczy pomnożyć N, Liczba stron.

W przypadku zwykłego pięciokąta z boku A, obwód P to:

P = 15a

Jeśli jest to nieregularna liczba, w której różni się miara boków, obwód dodaje długość wszystkich stron.

Jeśli chodzi o ten obszar, możemy go obliczyć na kilka sposobów. Na przykład mamy formułę, która pozwala jej uzyskać, znając długość a jego boków:

Wykonując wskazane operacje, pozostaje w przybliżeniu:

A = 17 6426⋅A²

Istnieje inna opcja, mającą zastosowanie do zwykłych wielokątów. Chodzi o podzielenie ich na trójkąty podstawowe równe wielokątom. Wysokość trójkąta jest długością apothem l_DO, zdefiniowane powyżej.

Obszar wspomnianego trójkąta jest obliczany z dobrze znaną wzorem: podstawa x wysokość /2. W ten sposób obszar pojedynczego trójkąta jest:

Obszar = a. L_DO /2

Aby mieć całkowitą powierzchnię wielokąta, wystarczy pomnożyć liczbę stron n, która w tym przypadku wynosi 15:

A = 15⋅a⋅ l_DO /2

A ponieważ obwód figury wynosi p = 15⋅a, następnie:

A = p⋅ l_DO /2

Piagonals

Piagonals to segmenty, które łączą dwa nieobserwowe wierzchołki, jak podano powyżej. Wiedzieć, ile przekątnych ma zwykły wielokąt N Strony, w tym Pentadecágono, istnieje następujący formuła:

Gdzie D jest liczbą przekątnych.

Teraz zastępujemy n = 15, aby uzyskać całkowitą przekątę:

Może ci służyć: zwykłe wielokąty: właściwości, elementy, kąty, przykłady

D = [15 × (15-3)]/2 = 90 przekątnych.

Konstrukcja z regułą i kompasem

Pentadecágono jest zbudowany z reguł i kompasów, zaczynając od obwodu. 360º należy podzielić na 15 równych części 24º. Najpierw konstrukcje pomocnicze wskazane w animacji są przeprowadzane w celu uzyskania kąta 60º, który jest podzielony z kolei na 36º i 24º.

Rysunek 3. Konstrukcja z regułą i kompasem zwykłego Pentagonu. Źródło: Wikimedia Commons.

Ćwiczenie rozwiązane

Jeśli obwód pentadecágono zarejestrowany w kręgu promienia r wynosi 12,56 cm. Oblicz:

a) radio.

b) Twój obszar.

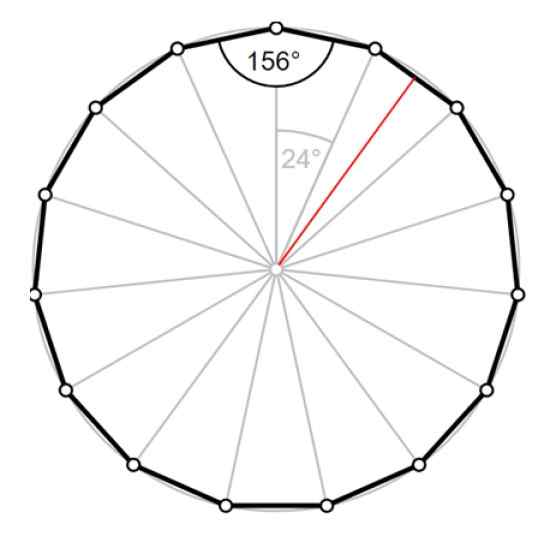Rysunek 4. Pentadecágono: kąt centralny, kąt wewnętrzny i czerwony apotema. Źródło: Wikimedia Commons/F. Zapata.

Rozwiązanie

Obwód wynosi p = 15⋅a = 12.Dlatego 56 cm Strona pentadecágono to 0.8373 cm. Radio Możemy to obliczyć za pomocą jednego z trójkątów na rycinie 4.

Apothem l_DO odpowiada wysokości trójkąta, narysowanego na czerwono, co dzieli kąt 24º na dwa kąty po 12º.

Istnieją dwa prawe trójkąty o wewnętrznym kącie 12º, a do każdego z nich możemy zastosować trygonometrię, aby znaleźć hipotenus, czyli długość R promienia.

Tą drogą:

Sen 12º = (a /2) /r

R = (a /2) /sen 12º = (0.8373 cm / 2) / Sen12º = 2.01 cm.

Rozwiązanie b

Możemy obliczyć obszar Pentadecágono przy użyciu wzoru:

A = p⋅ l_DO /2

Znamy już obwód p = 12.56 cm, a długość apothem jest obliczana przez styczną lub cosinus 12º:

Cos 12º = L_DO / R

L_DO = R. cos 12 º = 2.01 cm. cos 12 º = 1.97 cm

Zastąpienie:

A = 12.56 cm⋅ 1.97 cm /2 = 12.35 cm²

Bibliografia

1. Alexander, zm. 2013. Geometria. 5. Wydanie. Cengage Learning.
2. Naucz się matematyki. Liczby geometryczne. Odzyskane z: Rodrigoanchorena.Wixsite.com.
3. Sangaku Maths. Elementy wielokąta i jego klasyfikacja. Odzyskany z: sangakoo.com.
4. Wikipedia. Pentadecágono. Odzyskane z: jest.Wikipedia.org.
5. Wolfram Math World. Pentadecagon. Odzyskane z: Mathworld.Wolfram.com.