Pascalina lub Pascal Machine

Wyjaśniamy, czym jest Pascalina, jej historia, cechy i funkcjonowanie

Pascal de Pascal (1652). Źródło: Rama, CC BY-SA 3.0 fr, przez wikimedia Commons

Co to jest Pascalina?

Pascalina Jest to kalkulator mechaniczny, stworzony przez francuskiego naukowca i filozofa Blaise Pascal (1623-1661), około 1642 r., Mając zaledwie 19 lat. Nazwa „Pascalina” została nadana na jego cześć, chociaż nazywała się także „maszyną arytmetyczną”.

Dzięki systemowi przekładni wykonanej z żelaza i starannie wyartykułowanej, Pascalina jest w stanie dodać i odejmować, będąc prekursorem obecnych kalkulatorów. I podobnie jak te, Pascalina ma interfejs wprowadzania danych, które zamiast klawiszy wykorzystują serię ponumerowanych obrotowych dysków, aby wskazać wartość pozycyjną każdej cyfry: jednostki, dziesiątki, setki i więcej.

Numerowane dyski są wyposażone w otwory, w których wprowadza się pręta lub sztylet, aby przejść przez kroki.

Wewnętrzny mechanizm składa się z serii delikatnie sprzężonych kół zębów, które poruszają. Niektóre okna znajdujące się na dyskach, umożliwiają obserwowanie wartości, które nabywają te liczby.

Historia

Od dzieciństwa Pascal już zademonstrował swoje wielkie umiejętności intelektualne, więc jego ojciec, sędzia i matematyk Etienne Pascal postanowił dać mu najlepszą możliwą edukację. W 1642 r. Etienne Pascal została wysłana w celu podniesienia podatków w Rouen w Normandii, na północ od Francji, dzieło, które nie było łatwe.

Blaise Pascal, zdeterminowana, aby pomóc ojcu, zaprojektować i zbudować maszynę, która za pomocą mechanicznych biegów była w stanie obrócić niektóre koła do wykonywania i pokazania operacji sum i odejmowania. To urządzenie nazywało się „Pascalina”.

Blaise Pascal

W przypadku Pascalina mnożenie i podziały mogą być również przeprowadzane, ale nie bezpośrednio, ale poprzez kolejne sumy i odejmowanie.

Może ci służyć: gwiezdny lub sidereh dzień

Koszt produkcji Pascalina był jednak bardzo wysoki, więc wynalazek pozostał niezauważony przez większość w tym czasie. Ci, którzy mogli sobie pozwolić, wolą pozostawić go w domu i nie używać go do rutynowej pracy, więc prawie wszyscy nadal rozwiązywali swoje działalność w tradycyjny sposób.

Mechanizm Pascalina powinien być bardzo precyzyjny, więc kalkulator działał poprawnie, ale często przestał działać. A Pascal był jedynym, który mógł go naprawić za każdym razem, gdy tak się stało.

Pascal nadal poprawiał swój projekt w ciągu najbliższych 10 lat, osiągając około 50 Pascalinas, z czego dwa są zachowane: jeden jest w Niemczech, w Muzeum Zwinger, w Dresde, Niemczech, a drugi w Musée des Arts et Métiers, w Paryżu.

Charakterystyka i funkcja Pascalina

Pascalina ma cechy wspólne dla dzisiejszych kalkulatorów, jak stwierdzono na początku. Oczywistą różnicą jest to, że Pascalina współpracuje z elementami mechanicznymi, których regulacja musi być doskonała, podczas gdy dzisiejsze kalkulatory działają przez elektronikę.

Zasadniczo Pascalina ma:

• Interfejs do wprowadzenia danych, składający się z tarczy obsługiwanych przez stiletto.
• Wewnętrzny mechanizm wykorzystywany do przetwarzania tych danych, na podstawie biegów i mobilnych zębów.
• Panel, który pokazuje wyniki, z oknami rejestracyjnymi, aby docenić ruch wprowadzony na tarcze i obserwować wyniki.

Sumy są przeprowadzane bezpośrednio, przesuwając tarcze, aby wprowadzić każdą cyfrę dodatków. Jednak odejmowanie nie odbywa się bezpośrednio, ale w pewnym sensie, że zasadniczo jest dość ciekawy: uzupełnienie Pascalino, które wyjaśniono poniżej:

Uzupełnij do 9 lub Pascalino

Uzupełnienie do 9 jest techniką numeryczną, która przekształca odejmowanie w sumy, łatwiejsze do rozwiązania z układem mechanicznym zaimplementowanym przez Pascal.

Może ci służyć: schemat przepływu

Na przykład, jeśli chcesz rozwiązać operację A - B, dodaje „A” z uzupełnieniem Pascalino „B”, a wynikiem tej operacji jest poszukiwane odejmowanie.

Najpierw wyjaśniono, jak znaleźć uzupełnienie do 9 dowolnej liczby n. Jest to bardzo proste, jest odejmowane od 9 każdej cyfry tej liczby, jak pokazano w następujących przykładach:

• Niech n = 20, jego uzupełnienie do 9 robi: 99 - 20 = 79
• Dla n = 347 musisz zrobić: 999 -347 = 652
• Jeśli n = 7, jego uzupełnienie do 9 wynosi 2.

Odejmowanie przez uzupełnienie do 9

Załóżmy teraz, że chcesz wykonać następującą operację:

1246 - 822

Następujące kroki są następujące:

Krok 1: Znajdź uzupełnienie do 9 skradzionego, czyli 822, czyli 999–822 = 177.

Krok 2: Wykonaj sumę minuend i uzupełnienie do 9 wcześniej znalezionych: 1246 + 177 = 1423, obserwuj dobrze po lewej stronie w wyniku wyniku.

Krok 3: Żądana operacja odejmowania wynosi 423 + 1 = 424.

Czytelnik może sprawdzić wynik za pomocą wspólnego kalkulatora!

Jeśli minuend jest mniejszy niż odejmowanie, kontynuuj na przykład, aby przeprowadzić:

267 - 592

Krok 1: Znajdź uzupełnienie do 9 podsekcji 592, czyli 999 - 592 = 407.

Krok 2: Dodaj minuend i uzupełnij do 9 skradzionych: 267 + 407 = 674.

Krok 3: Oblicz uzupełnienie do 9 wyników: 999 - 674 = 325

Krok 4: Dodaj znak ujemny do wyniku: -325 i jest to żądane odejmowanie.

Na pierwszy rzut oka wydaje się bardziej skomplikowane, aby odejmować w ten sposób, ale dzięki systemowi zębów jest łatwiejsze.

Jak działa Pascalina?

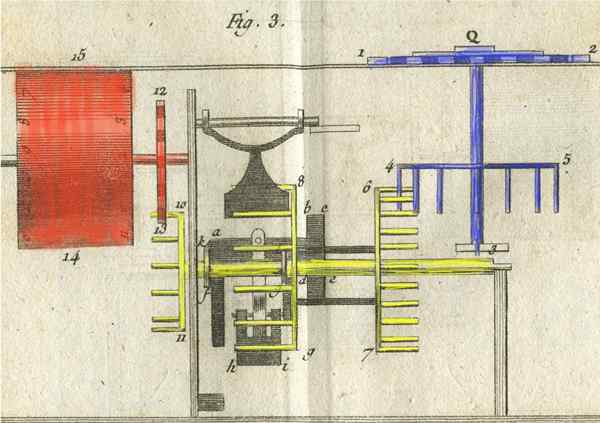
Wewnętrzny mechanizm Pascalina

Pascalina składa się zasadniczo z systemu przekładni, który obraca 10 cylindrów wskazujących liczby. Każdy cylinder łączy dwie serie liczb, a każda seria wynosi od 0 do 9.

Cylinder skrajnej prawicy wskazuje jednostki, które podążają za kilkadziesiątami, następującymi setkami i tak dalej. Kiedy jeden z cylindrów obraca się z całkowitym zakrętem, mechanizm sprawia, że ​​na lewym postępie. Im więcej cyfr ma postać, tym więcej kół i cylindrów muszą się poruszać, co daje pojęcia o delikatnym mechanizmie wewnętrznym Pascalina.

Może ci służyć: 11 przykładów badań terenowych

Wprowadzenie liczb jest wykonane przez tarcze ponumerowane poza urządzeniem, z igłą lub szpilką, zaprojektowaną do tego celu. Istnieją tarcze dla jednostek, dziesiątek, setek i więcej, odpowiadające każdemu z cylindrów.

Teraz zobaczysz, jak przeprowadzić operacje.

Dodać

Załóżmy, że chcesz wykonać następującą operację z Pascalina:

25 + 14

Ze wszystkimi zainicjowanymi pokrętłami w 0, pokrętło 2 jednostek lub kroków porusza się, a pokrętło jednostek porusza się w 5 krokach. Dzięki temu wprowadzono pierwsze dodanie.

Następnie porusza się pokrętło jednostki Tens 1, a jednostki do 4. Wynik to: 39.

Po przyjęciu pełnego zakrętu do 8, a koła dodają niezbędne okrążenia do górnych cyfr, aby pokazać wynik.

Odejmować

Aby odejmować, wszystkie tarcze są umieszczane do 9, ponieważ mechanizm wpływa na odjęcie przez dopełnienie do 9, jak wskazano w poprzednim rozdziale. Użytkownik nie musi obliczać uzupełnienia, mechanizm sam w sobie czyni, inicjowanie DALS o 9.

Na przykład chcesz zrobić:

67 - 21

Przebiega w taki sam sposób, jak w sumie, to znaczy pokrętło dziesiątek jest obracane w 6 krokach, a jednostki jest obracane w 7 krokach. W ten sposób wprowadza się wartość minuend. Następnie pokrętło 2 kroków i jednej z jednostek 1 jest obrócony. Wynik to 46, w jaki sposób czytnik może sprawdzić.