Równoległościan

Równoległoboki są sześcioosobowymi postaciami geometrycznymi, w których przeciwieństwa są do siebie równoległe. Przykład: cegła, pudełko na buty, wiadro itp.

Co jest równoległym?

A równoległościan Jest to korpus geometryczny utworzony przez sześć twarzy, którego główną cechą jest to, że wszystkie jego twarze są równoległobokami, a także przeciwne twarze są równoległe do siebie. Jest to powszechny wielościan w naszym codziennym życiu, ponieważ możemy go znaleźć w pudełkach na buty, kształt cegły, kształcie mikrofalowej itp.

Będąc wielościennym, równoległobrzewane zawiera skończoną objętość, a wszystkie jego twarze są płaskie. Jest częścią grupy pryzmatów, które są te wielościany, w których wszystkie jej wierzchołki są zawarte w dwóch równoległych płaszczyznach.

Elementy równoległości

Twarze

Są to każdy z regionów utworzonych przez równoległoboki, które ograniczają równoległoboki. Równoległoboczny ma sześć twarzy, gdzie każda twarz ma cztery sąsiednie twarze i odwrotnie. Ponadto każda twarz jest równoległa z odwrotnie.

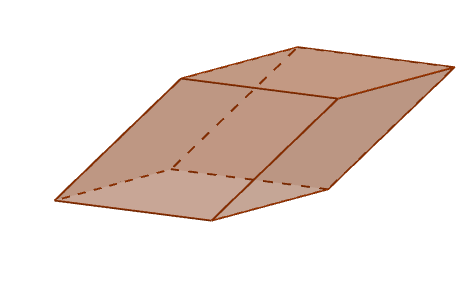Perspektywa równoległości

Krawędzie

Są to wspólna strona dwóch twarzy. W sumie równoległoboczny ma dwanaście krawędzi.

Wierzchołek

Jest to wspólny punkt trzech twarzy, które są sąsiadujące od dwóch do dwóch. Równoległość ma osiem wierzchołków.

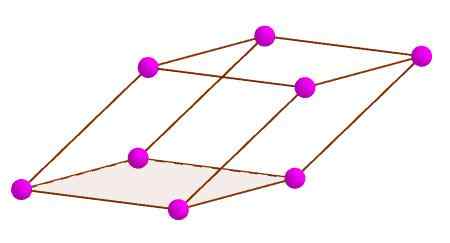Wierzchołki równoległości

Przekątna

Biorąc pod uwagę dwie twarze równoległego do siebie, możemy narysować segment linii, który przechodzi od wierzchołka jednej twarzy do przeciwnego wierzchołka drugiego.

Ten segment jest znany jako równoległość po przekątnej. Każdy równoległość ma cztery przekątne.

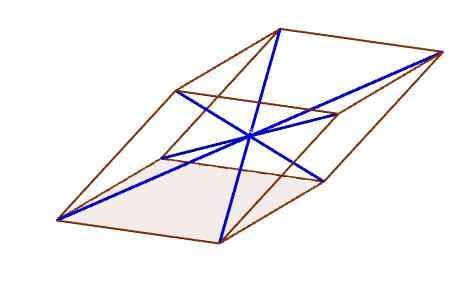Po przekątnej równoległości

Centrum

Jest to punkt, w którym przecinają się wszystkie przekąski.

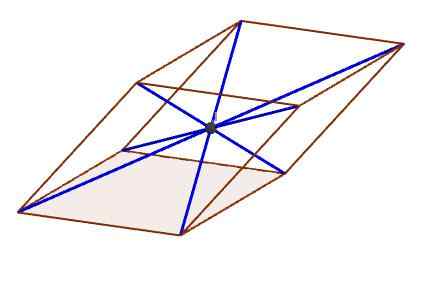Punkt na rysunku wskazuje środek, w którym przecinają się wszystkie przekąski

Charakterystyka równoległości

Jak już wspomnieliśmy, ten geometryczny korpus ma dwanaście krawędzi, sześć twarzy i osiem wierzchołków.

W równoległości można zidentyfikować trzy zestawy utworzone przez cztery krawędzie, które są do siebie równoległe. Ponadto krawędzie tych zestawów są również zgodne z właściwością posiadania tej samej długości.

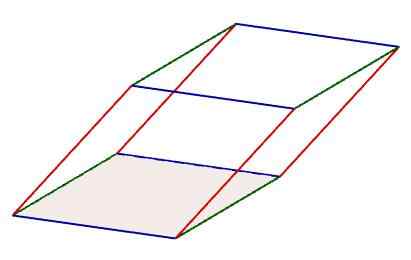Charakterystyka równoległości

Kolejna nieruchomość.

Ponadto równoległoboki, które są wypukłe wielosedry, są zgodne z twierdzeniem Eulera dla wielościów, co daje nam związek między liczbą twarzy, liczbą krawędzi i liczbą wierzchołków. Ten związek jest podawany w postaci następującego równania:

C + V = a + 2

Ta funkcja jest znana jako cecha Eulera. Gdzie C jest liczbą twarzy i liczbą wierzchołków i liczby krawędzi.

Rodzaje paralleepípedos

Możemy sklasyfikować równoległości na podstawie ich twarzy, na następujących typach:

Orthoedro

Są równoległymi, w których ich twarze składają się z sześciu prostokątów. Każdy prostokąt jest prostopadły z tymi, z którymi dzieli się krawędzi. Są najczęstsze w naszym codziennym życiu, to jest zwykła forma butów i cegiełek.

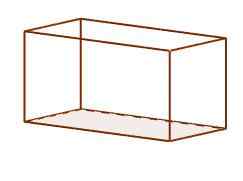Orthoedro równoległe

Zwykła kostka lub sześciokątne

Jest to szczególny przypadek poprzedniego, w którym każda z twarzy jest kwadratem.

Może ci służyć: elipsaZwykła kostka lub sześciokątne

Kostka jest również częścią ciał geometrycznych zwanych stałymi platońami. Platoniczna substancja stała to wypukły wielościan, dzięki czemu zarówno jego twarze, jak i wewnętrzne kąty są sobie równe.

Romboedro

Jest to równoległość, która ma romb. Te rombki są sobie równe, ponieważ dzielą krawędzie.

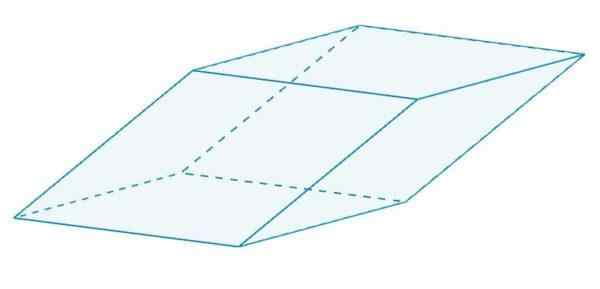Romboedro

Romboiedro

Jego sześć twarzy to Rhomboid. Przypomnijmy, że romboid to czterokątny wielokąt i cztery kąty, które są równe od dwóch do dwóch. Rhomboids to równoległoboki, które nie są ani kwadratowe, ani prostokąty, ani romb.

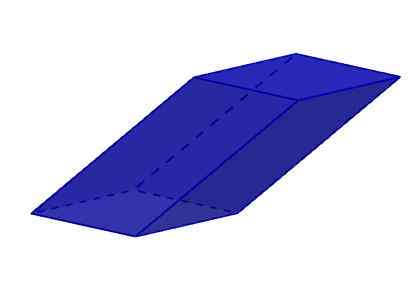Romboiedro

Z drugiej strony ukośne równoległości są te, w których co najmniej jedna wysokość nie pasuje do krawędzi. W tej klasyfikacji możemy dołączyć Rhomboedros i Rhomboiedros.

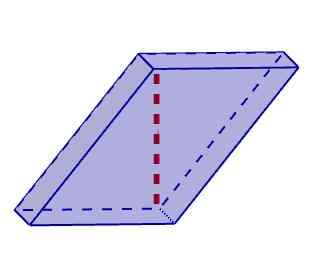Ukośny równoległość

Obliczenia po przekątnej

Aby obliczyć przekątną ortoedro, możemy użyć twierdzenia Pitagorasa dla R³.

Przypomnij sobie, że Orthoedro ma charakterystykę, że każda strona jest prostopadła z bokami, która dzieli Edge. Z tego faktu możemy wywnioskować, że każda krawędź jest prostopadła z tymi, które dzieli wierzchołek.

Aby obliczyć długość przekątnej ortoedro, postępujemy w następujący sposób:

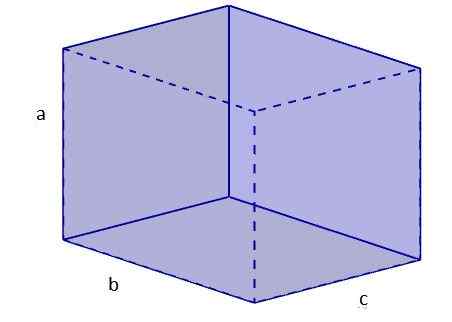
1. Obliczamy przekątną jednej z twarzy, które będziemy umieścić według podstawy. Do tego używamy twierdzenia Pitagorasa. Nazwijmy to Diagonal D_B.

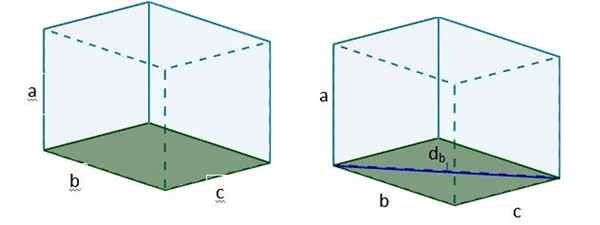
2. Następnie z D_B Możemy utworzyć nowy trójkąt prostokąta, tak że hipotenusa tego trójkąta jest poszukiwana po przekątnej.

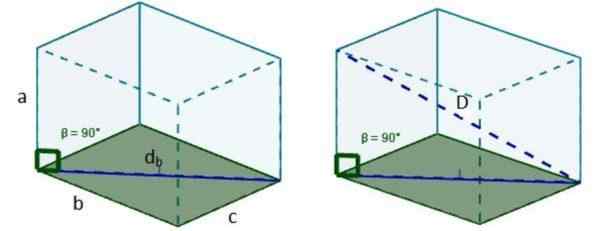
3. Ponownie używamy twierdzenia Pitagorasa i mamy, że długość tej przekątnej wynosi:

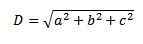
Innym sposobem obliczania przekątnej w bardziej graficzny sposób jest suma wolnych wektorów.

Przypomnij sobie, że dwa wolne wektory A i B są dodawane przez umieszczenie ogona wektora B z końcem wektora A.

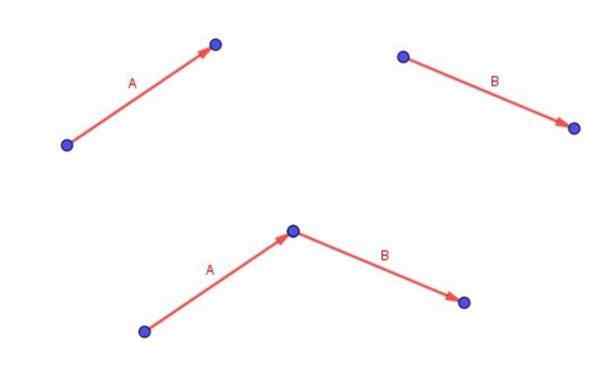
Wektor (a + b) jest tą, która zaczyna się w ogonie a i kończy na końcu b.

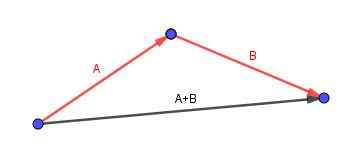
Rozważ równoległość, do której chcemy obliczyć przekątną. Identyfikujemy krawędzie z wygodnymi wektorami zorientowanymi.

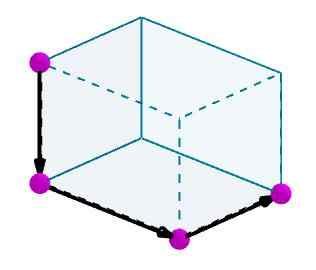
Następnie dodajemy te wektory, a wynikowym wektorem będzie przekątna z równoległości.

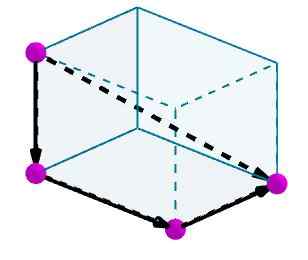
Obszar równoległości

Obszar równoległości jest podany przez sumę każdego z obszarów jego twarzy.

Jeśli określamy jedną z boków jako podstawy,

DO_L + 2_B = Całkowity obszar

Gdzie_L Jest równy sumie obszarów wszystkich stron sąsiadujących z podstawą, zwaną obszarem bocznym i_B Jest to obszar podstawowy.

W zależności od rodzaju równoległości, z jaką możemy przepisać wspomnianą formułę.

Obszar ortoedro

Jest podawany przez formułę

A = 2 (AB + BC + CA).

Przykład 1

Biorąc pod uwagę następujące ortoedro, z bokami a = 6 cm, b = 8 cm i c = 10 cm, oblicz powierzchnię równoległości i długość jego przekątnej.

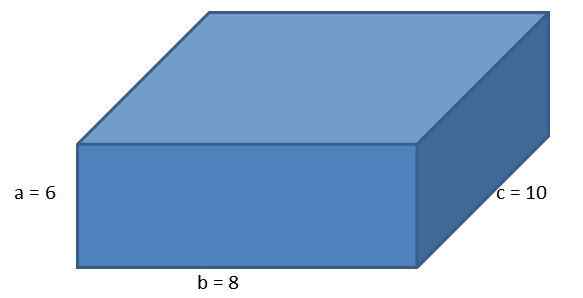
Używając formuły dla obszaru ortoedro, musimy

A = 2 [(6) (8) + (8) (10) + (10) (6)] = 2 [48 + 80 + 60] = 2 [188] = 376 cm².

Zauważ, że jako ortoedro jest długością każdego z czterech przekątnych jest taka sama.

Może ci służyć: całka nieokreślona: właściwości, zastosowania, obliczenia (przykłady)

Używając twierdzenia Pitagorasa dla przestrzeni, musimy

D = (6² + 8² + 10²)^1/2 = (36 + 64 + 100)^1/2 = (200)^1/2

Obszar kostki

Ponieważ każda krawędź ma tę samą długość, mamy, że a = b i a = c. Zastąpienie w poprzednim formule, którą mamy

A = 2 (aa + aa + aa) = 2 (3a²) = 6a²

A = 6a²

Przykład 2

Pudełko konsoli gier ma kształt kostki. Jeśli chcemy owinąć to pudełko papierem prezentowym, ile papieru wydalibyśmy, wiedząc, że długość krawędzi kostki wynosi 45 cm?

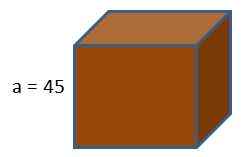
Korzystając z formuły obszaru kostki

A = 6 (45 cm)² = 6 (2025 cm²) = 12150 cm²

Obszar Rhomboedro

Ponieważ wszystkie jego twarze są takie same, wystarczy obliczyć obszar jednego z nich i pomnożyć go przez sześć.

Mamy, aby obszar rombowy można obliczyć przez jego przekątne z następującym wzorem

DO_R = (DD)/2

Używając tej formuły, następuje, że całkowita powierzchnia Rhomboedro jest

DO_T = 6 (DD)/2 = 3DD.

Przykład 3

Twarze następnego Rhomboedro powstają przez romb, którego przekątna wynosi d = 7 cm i d = 4 cm. Twój obszar będzie

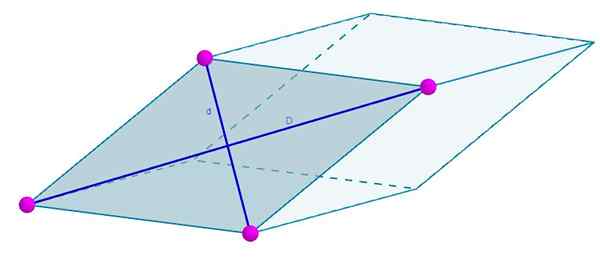
A = 3 (7 cm) (4 cm) = 84 cm².

Obszar Rhomboiedro

Aby obliczyć obszar Rhomboiedro, musimy obliczyć obszar romboidów, które go komponują. Gdy równoległości wypełniają właściwość, którą mają przeciwne strony, możemy powiązać boki u trzech rówieśników.

W ten sposób mamy, że twój obszar będzie

DO_T = 2b₁H₁ + 2b₂H₂ + 2b₃H₃

Gdzie b_Siema czy podstawy związane z bokami i h_Siema jego względna wysokość odpowiadająca wspomnianym bazom.

Przykład 4

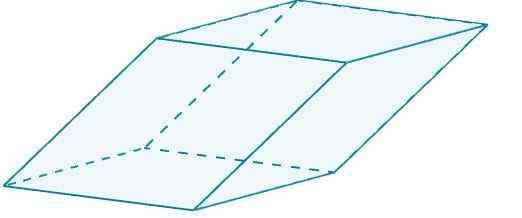
Rozważ następujące równoległość,

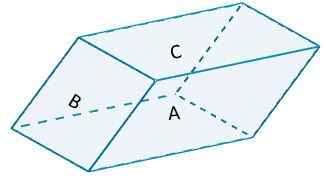
gdzie strona a i strona a '(ich przeciwna strona) są oparte na b = 10 i na wysokość h = 6. Oznaczony obszar będzie miał wartość

DO₁ = 2 (10) (6) = 120

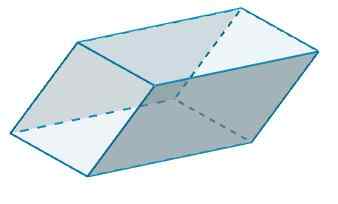
B i B 'mają b = 4 i h = 6, wtedy

DO₂ = 2 (4) (6) = 48

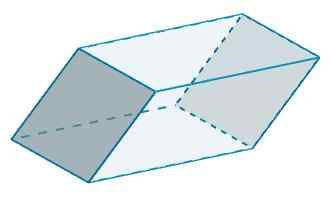
A c i c 'mają również b = 10 i h = 5,

DO₃ = 2 (10) (5) = 100

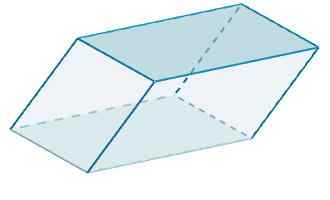
Wreszcie obszar Rhomboiedro jest

A = 120 + 48 + 100 = 268.

Objętość równoległości

Formuła, która daje nam objętość równoległości, jest iloczynem obszaru jednej z jego twarzy ze względu na wysokość odpowiadającą wspomnianej twarzy.

V = a_CH_C

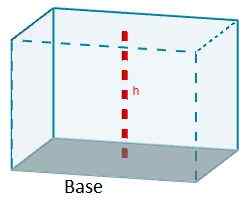
W zależności od rodzaju równoległości, ten wzór można uprościć.

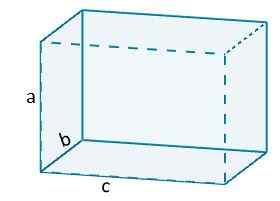
Zatem mamy na przykład, że objętość ortoedro byłaby podana przez

V = ABC.

Gdzie A, B i C reprezentują długość krawędzi ortoedro.

Aw konkretnym przypadku kostki jest

V = a³

Przykład 1

Istnieją trzy różne modele dla pudełek z ciasteczkami i chcesz.

Pierwszy to kostka, której krawędź ma długość a = 10 cm.

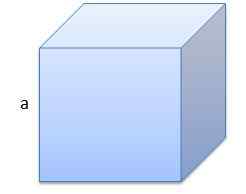
Jego objętość będzie V = 1000 cm³

Drugi to b = 17 cm, c = 5 cm, d = 9 cm.

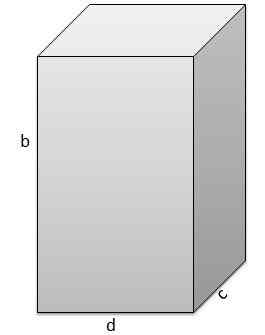
I dlatego jego objętość wynosi v = 765 cm³

A trzeci ma e = 9 cm, f = 9 cm i g = 13 cm.

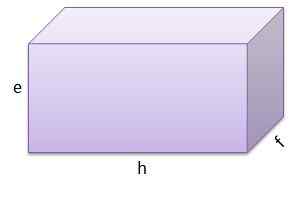
A jego objętość to v = 1053 cm³

Może ci służyć: rodzaje kątów, cechy i przykłady

Dlatego pudełko o największym objętości jest trzecim.

Inną metodą uzyskania objętości równoległości jest ucieczka do algebry wektorowej. W szczególności produkt Triple Scalar.

Jedną z geometrycznych interpretacji potrójnego produktu skalarnego jest objętość równoległości, których krawędzi są trzy wektory, które mają ten sam wierzchołek co punkt wyjścia.

W ten sposób, jeśli mamy równoległość i chcemy wiedzieć, jaki jest jego objętość, wystarczy reprezentować go w układzie współrzędnych w R³ Zbiega jeden ze swoich wierzchołków z pochodzeniem.

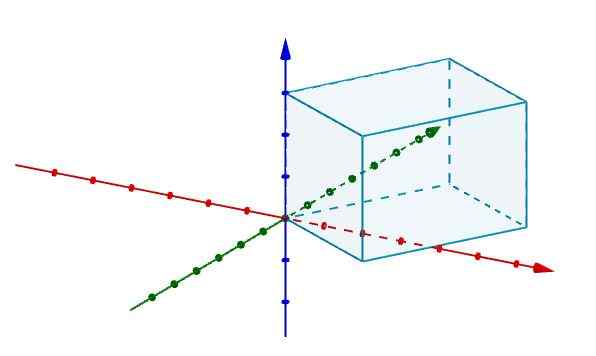
Następnie reprezentujemy krawędzie, które zgadzają się na pochodzeniu z wektorami, jak pokazano na rysunku.

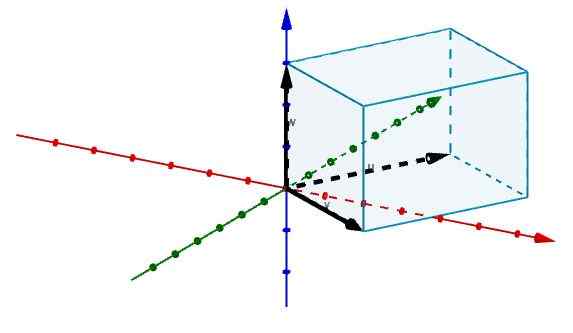
I w ten sposób mamy, że objętość wspomnianego równoległości jest podana przez

V = | AXB ∙ C |

Lub równoważne, objętość jest wyznacznikiem macierzy 3 × 3, utworzonej przez składniki wektorów krawędziowych.

Przykład 2

Reprezentując następujące równoległość w R³ Widzimy, że wektory, które go określają, są następującymi

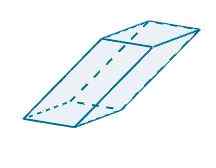
u = (-1, -3,0), v = (5, 0, 0) i w = (-0.25, -4, 4)

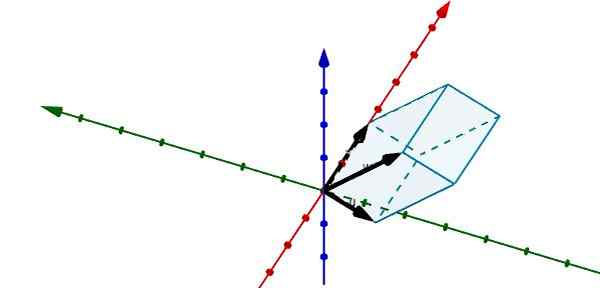
Korzystanie z potrójnego produktu skalarnego, który mamy

V = | (Uxv) ∙ w |

Uxv = (-1, -3,0) x (5, 0, 0) = (0,0, -15)

(Uxv) ∙ w = (0,0,- 15) ∙ (-0.25, -4, 4) = 0 + 0 + 4 ( - 15) = - 60

To stwierdza, że ​​v = 60

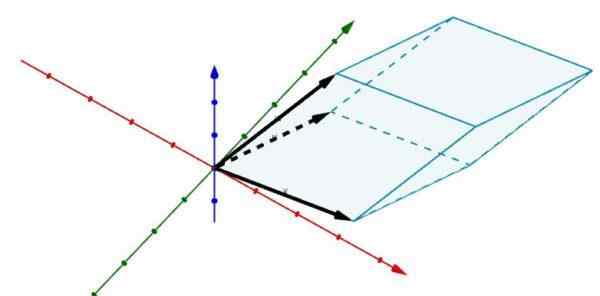
Rozważ teraz następujące równoległości w R³ których krawędzie są określone przez wektory

A = (2, 5, 0), b = (6, 1, 0) i c = (3, 4, 4)

Używanie determinantów daje nam to

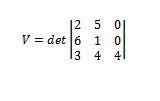
Zatem mamy, że objętość wspomnianego równoległości wynosi 112.

Oba są równoważnymi sposobami obliczania objętości.

Idealny równoległość

Jest znany jako cegła Euler (lub blok eulera) do ortoedro, który spełnia właściwość, że zarówno długość jego krawędzi, jak i długość przekątnej każdej z jego twarzy są liczbami całkowitymi.

Podczas gdy Euler nie był pierwszym naukowcem, który studiował ortoederów, którzy spełniają tę nieruchomość, znalazł o nich interesujące wyniki.

Najmniejsza cegła Eulera została odkryta przez Paula Halcke'a (1662-1731), a długości jego krawędzi wynoszą A = 44, B = 117 i C = 240.

Otwarty problem w teorii liczb jest następujący:

Czy są idealni ortoederowie?

Obecnie to pytanie wciąż nie ma odpowiedzi, ponieważ nie było możliwe udowodnienie, że nie ma ciał, ale nikogo nie znaleziono.

Do tej pory wykazano, że idealnie wykonuje równoległość. Pierwszy, który został odkryty, ma jako długość krawędzi, wartości 103, 106 i 271.

Bibliografia

1. Guy, r. (1981). Nierozwiązane problemy w teorii liczb. Skoczek.
2. Landaverde, f. D. (1997). Geometria. Postęp.
3. Leithold, L. (1992). Obliczenia z geometrią analityczną. Harla, s.DO.
4. Rendon, a. (2004). Rysunek techniczny: Notebook aktywności 3 2. matur. Tebar.
5. Resnick, r., Halliday, d., I Krane, K. (2001). Vol Fizyka. 1. Meksyk: Continental.