Zamówiona para

Co to jest uporządkowana para?

Uporządkowana para lub duet Jest to zestaw dwóch elementów, które są zapisane zgodnie z zamówieniem ustanowionym przez określone kryterium. Wspomniane kryteria określają, który z dwóch elementów przechodzi pierwszy, a który idzie później.

Uporządkowana para jest oznaczona jako (x, y), gdzie „x” jest pierwszym elementem pary, a „y” to drugi, również nazywany składniki. Ogólnie (x, y) to nie jest ten sam schludny moment obrotowy (y, x). A oprócz kolejności kolejną ważną cechą uporządkowanych par jest równość: dwie uporządkowane pary (a, b) i (c, d) są takie same tylko wtedy, gdy a = c i b = d.

Rysunek 1.- Dzięki schludnym parom szczeniak wie, że kości są pochowane w lokalizacjach (3,1) i (-4,2), a jego dom jest w (0,0). Źródło: f. Zapata.

Przykładami uporządkowanych par byłyby te, które składają się z wieku i waga kursu studentów matematyki. Uporządkowana para (15, 62) odpowiada 15 -letniej uczniowi, innej od mało prawdopodobnej pary (62,15).

Koncepcja uporządkowanego momentu obrotowego jest bardzo ważna w różnych obszarach matematyki, takich jak płaszczyzna kartezjańska, ułamki, wektory w płaszczyźnie, relacje i funkcje. Ważnym aspektem jest to, że ich elementy niekoniecznie mają numeryczne, na przykład można je zamówić:

• Miasto krajowe
• Imię Nazwisko
• Żona mąż

I wiele innych kombinacji.

Przykłady uporządkowanych par

Frakcje

Ułamek jest reprezentowany jako iloraz dwóch liczb całkowitych P/Q, na przykład ułamek ½, co jest równoważne liczbie dziesiętnej 0.5.

Jednak frakcja ta nie jest jedyną, która reprezentuje dziesiętne 0.5, podobnie jak następujące:

2/4; 3/6; (-2)/(-4); 20/40; (-1)/(-2)…

W ten sposób każda frakcja może być reprezentowana jako para uporządkowana (p, q), gdzie p i q są całe, a p zajmują pozycję licznika i q wyznaczającej mianownik. Istnieje ważne ograniczenie i że Q (mianownik) musi być inna od 0, ponieważ ułamki formy P/0 nie są zdefiniowane.

Może ci służyć: Zestaw skończony: właściwości, przykłady, rozwiązane ćwiczenia

Kolejnym ważnym warunkiem jest to, że dwie frakcje A/B i C/D są równe, o ile się spełni, że:

A ∙ d = b ∙ c

Funkcje i jej wykresy

Funkcję można wyrazić jako zestaw schludnych par. Na przykład, wykresując funkcję w płaszczyźnie kartezjańskiej, pierwszym element. To jest uporządkowana para.

Dla funkcji y = f (x) uporządkowany moment obrotowy można wyrazić jako [x, f (x)]]. Rozważmy na przykład zestaw początkowy:

A = 1, 2, 3, 4

W tym zestawie są pierwsze elementy uporządkowanej pary zgodnie z funkcją y = x². Zestaw drugich komponentów to:

B = 1, 4, 9, 16

A uporządkowane pary są tworzone:

(1,1); (2,4); (3, 9); (4; 16)

Szacunek.

Wektory w płaszczyźnie

Wektory mogą być reprezentowane w płaszczyźnie kartezjańskiej za pomocą uporządkowanych par, gdzie pierwszy element reprezentuje składnik poziomy „x”, a drugi komponent pionowy „Y”. Aby odróżnić wektory od punktów w płaszczyźnie, są one oznaczone odważnymi literami i zamiast w nawiasach używane są nawiasy kwadratowe, takie jak:

v =

Na przykład wektor v = ma składnik poziomy równy 4, a komponent pionowy równy 7. Jego wykres jest:

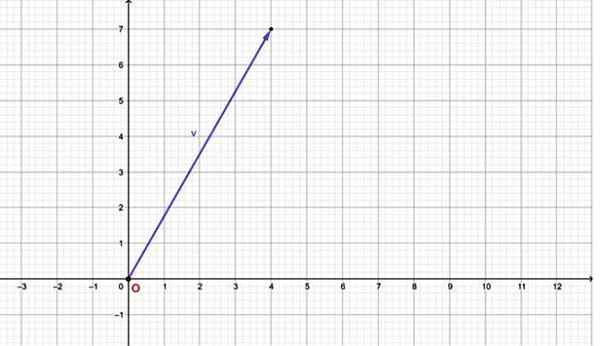Rysunek 2.- Wektor płaszczyzny można wyrazić za pomocą uporządkowanej pary. Źródło: f. Zapata.

Należy zauważyć, że ten wektor zbiega się z pochodzeniem układu współrzędnych (0,0). Jeśli wektor ma swoje pochodzenie w dowolnym innym punkcie, można go również wyrazić w postaci uporządkowanego momentu obrotowego przez pary uporządkowane, zobacz następujące sekcje.

Może ci służyć: hierarchia operacji

Zamówiono operacje PARES

Dodatek

Niech cele (a, b) i (c, d) będą parami (d). Nowy moment obrotowy uzyskuje się za pomocą swojej sumy zgodnie z:

(a, b)+(c, d) = (a+c, b+d)

Element neutralny

Neutralny element dodania uporządkowanych par jest moment obrotowy (0,0), ponieważ gdy dodaje on uporządkowaną parę (a, b), suma jest ta ostatnia:

(a, b) + (0,0) = (a, b)

Suma przeciwnego

Dodając uporządkowaną parę (a, b) z jego przeciwieństwem (-a, -b) uzyskuje się uporządkowany moment obrotowy (0,0):

(a, b) + (-a, -b) = (0,0)

Komutność

Kolejność dodatków nie zmienia sumy:

(a, b) + (c, d) = (c, d) + (a, b)

Asocjacyjność

Wynik dodania trzech uporządkowanych par nie jest zmieniany po zgrupowaniu w celu wykonania operacji:

[(a, b) + (c, d)] + (e, f) = (a, b) + [(c, d) + (e, f)]

Odejmowanie uporządkowanych par

Niech cele (a, b) i (c, d) będą, odejmowanie jest przeprowadzane w następujący sposób:

(a, b)-(c, d) = (a-c, b-d)

Produkt

W produkcie istnieją dwie opcje: i) pomnóż moment obrotowy uporządkowane przez stał.

Mnożenie przez stałą

Niech K będzie stałą, a uporządkowany moment obrotowy (a, b) produkt między stałą a momentem obrotowym to:

K ∙ (a, b) = (k ∙ a, k ∙ b)

Mnożenie uporządkowanych par

Produkt między uporządkowanymi parami (a, b) i (c, d) jest przeprowadzany w następujący sposób:

(a, b) x (c, d) = (ac - bd, bc+ad)

Element neutralny

Neutralny element mnożenia wynosi (1.0), ponieważ poprzez pomnożenie dowolnego momentu uporządkowanego przez to, zgodnie z regułą mnożenia opisanego powyżej, oryginalny moment obrotowy to:

(a, b) x (1.0) = (a - 0, b + 0) = (a, b)

Może ci służyć: odwrotność multiplikatywna: wyjaśnienie, przykłady, rozwiązane ćwiczenia

Asocjacyjność

Ponieważ kolejność czynników nie zmienia produktu, można go pogrupować na różne sposoby, aby pomnożyć trzy lub więcej uporządkowanych par, a wynik jest taki sam:

[(a, b) x (c, d)] x (e, f) = (a, b) x [(c, d) x (e, f)]

Rozwiązane ćwiczenia

Ćwiczenie 1

Zamówiłeś pary (x², X-2) = (16, 2). Która jest wartością x?

Rozwiązanie

Zastosowanie równości uporządkowanych par jest uzyskiwane najpierw:

X² = 16 ⇒ x₁ = 4, x₂ = -4

Aby wiedzieć, które z dwóch wartości wybiorą, użycie:

X-2 = 2

x = 2 + 2 = 4

Dlatego żądana wartość x wynosi 4.

Ćwiczenie 2

Wyraź jako uporządkowana para wektora, który przechodzi od punktu (1, 3) do punktu (7, 11) i reprezentuj go graficznie.

Rozwiązanie

Być v Wektor przeszukał. Aby określić uporządkowaną parę, która ją reprezentuje i która zawiera jego współrzędne, współrzędne punktu przybycia i punkt pochodzenia są odjęte w tej kolejności. Więc:

v = =

Wektor jest następnie reprezentowany v jako ten, który przechodzi z (1.3) do (7, 11) i sprzęt v którego pochodzenie jest ustalone do pochodzenia układu współrzędnych (0,0). Jak widać, mają ten sam kierunek i znaczenie.

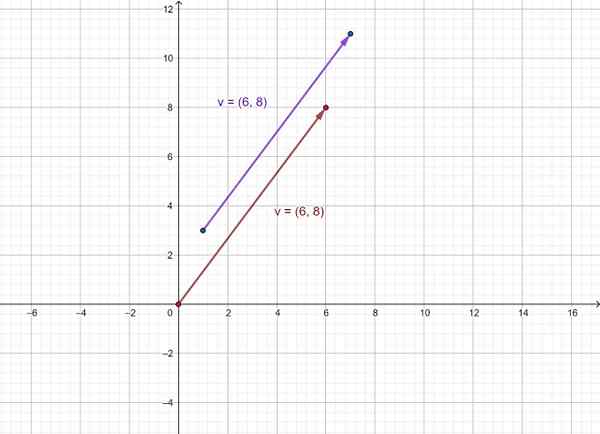Rysunek 3. Reprezentacja wektora jako parę uporządkowaną. Źródło: f. Zapata.

Bibliografia

1. Deepal. Zamówiona para. Odzyskane z: Deedai.org.
2. Mathemovil. Kartezjańska reprezentacja wektora przez uporządkowaną parę. Odzyskany z: Matemovil.com.
3. Varsity Tutorrs. Zamówiona para. Źródło: WarsityTorm.com
4. Priestri, Juan. Relacje i funkcje. Wydział Inżynierii. Departament Matematyki. Uniwersytet Buenos Aires. Źródło: tematy.fi.UBA.ar.
5. University of Denver. Relacje. Odzyskane z: matematyki.Ucdenver.Edu.