Trzy -wymiarowe fale koncepcji, typy i przykłady

Czy trzy -wymiarowe fale Te, które rozprzestrzeniają się w przestrzeni, na przykład fala dźwiękowa wytwarzana przez głośnik. Ta fala rozprzestrzenia się we wszystkich kierunkach, choć nie z taką samą intensywnością we wszystkich z nich.

Jeśli zakłócenie nastąpi w jednym punkcie w przestrzeni, to rozprzestrzenia się w trzech kierunkach przestrzennych, a przednie fronty fali są zamknięte, sferyczne, eliptyczne lub inne.

Trzy -wymiarowe fale wytwarzane przez głośnika

Z drugiej strony, jeśli miejsce, w którym pochodzą fale, to znaczy źródło ma rozkład płaski, wówczas zakłócenia będzie podróżować głównie w kierunku prostopadłym do tej płaszczyzny, tworząc fronty fali płaskiej fali.

[TOC]

Rodzaje trzech wymiarów fal

W trzech wymiarach fal fronty falowe są zestawem powierzchni zanurzonych w przestrzeni trójwymiarowej.

Teraz przód fali jest geometrycznym miejscem punktów kosmicznych osiągniętych przez początkowe zakłócenia, w tym samym czasie.

Zgodnie z symetrią frontu falowego, płaskie fale, płaskie fale, fale fali fali: płaskie fale, fale fali fali: fale płaskie, fale, cylindryczne fale, fale cylindryczne i fala. Jednak prawdziwe fale nie zawsze należą do tego typu, ponieważ nie mają tak wysokiego stopnia symetrii.

Płaskie fale

Płaska fala, która podróżuje w pozytywnym kierunku x szybko v, jest funkcjonalnie reprezentowana jako:

G (x, t) = f (x - v⋅t)

Ta fala nie ogranicza się do osi X, ale także rozciąga się na adresy I I z. Ale forma funkcjonalna wskazuje, że wszystkie punkty, które mają tę samą współrzędną x, niezależnie od współrzędnych (z, y), mają tę samą wartość G.

W tym przypadku fronty falowe są samolotami równoległymi do Z-i płaszczyzny, która szybko się rozwija v, co oznacza, że ​​płaska fala zajmuje wszystkie trzy -wymiar przestrzeni.

Wyrażenie reprezentujące płaską falę, która rozprzestrzenia się w dowolnym kierunku Lub szybko v, Gdzie Lub reprezentuje jednostkę starszych dyrektorów wektorów cos (α), cos (β) I cos (γ), Jest:

Może ci służyć: entalpia reakcji: definicja, termochemia, ćwiczenia

g = f (û • r - Vienta) = f (x cos (α) + i cos (β) + z cos (γ) - v⋅t)

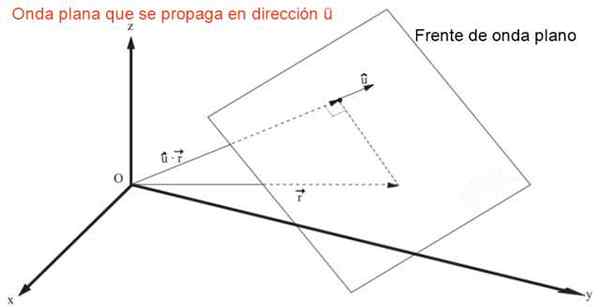Płaska front fala, który rozprzestrzenia się w trójwymiarowej przestrzeni szybko v. Źródło: f. Zapata.

Bezpośrednio łatwo wykazać, że poprzednie wyrażenie jest rozwiązaniem trójwymiarowego równania fali, równaniem w częściowych pochodnych drugiego rzędu liniowego:

∂_XxG + ∂_TakG + ∂_ZZG = (1/v²) ∂_TtG

Poprzednie równanie można zapisać bardziej kompaktowo za pomocą operatora Laplacian ∇²:

∇²G = (1/v²) ∂_TtG

Fale cylindryczne

Gdy początkowe zakłócenia jest rozmieszczone na linii prostej, fala rozprzestrzenia się w kierunku promieniowym prostopadłym do tej linii wypełniającej otaczającą ją trójwymiarową przestrzeń, z cylindrycznymi frontami falowymi.

Fale sferyczne

Gdy źródło jest punktualne, a medium, w którym fala trzywymiarowa jest propagowana, jest jednorodna i izotropowa (jego właściwości nie zmieniają się zgodnie z kierunkiem), wówczas fronty fali są koncentrycznymi sferami do punktu, w którym wystąpiło początkowe zakłócenia.

W przypadku fali sferycznej, w której intensywność fali jest identyczna we wszystkich kierunkach, funkcja opisująca zakłócenia zależy tylko od odległości R do źródła terminowego i czasu T.

W takim przypadku odpowiadający Laplacian to:

∇²G = (1/r²) ∂_R(R² ∂_RG)

Bycie równaniem fali:

∇²G = (1/v²) ∂_TtG

Ogólnym rozwiązaniem byłoby:

g (r, t) = (1/r) f (r - v⋅t) + (1/r) g (r + v⋅t)

W takim przypadku mówi się, że jest to fala sferyczna. Ale mogą istnieć warianty, jak to widać poniżej

Niezotropowe fale sferyczne

Może się również zdarzyć, że fala sferyczna, to znaczy z frontami falowymi utworzonymi przez koncentryczne kule do punktu centralnego, amplituda lub intensywność fali jest inna w różnych kierunkach.

Tak się dzieje, gdy centralne źródło fali jest bardziej wydajne w kierunku niż inne. 

Może ci służyć: fizyka przed Greków (Antigua Grecja)

Na przykład dźwięk wytwarzany przez klakson nie ma wszędzie takiej samej intensywności, nawet w przypadku punktów równości rogu.

Intensywność nie jest taka sama, chociaż sygnał zajmuje w tym samym czasie, aby osiągnąć te punkty. Jest to fala sferyczna, która ma nieferyczny wzór kierunkowy. 

Istnieją również fale sferyczne w przypadku fal elektromagnetycznych tworzonych przez antenę, ale mogą nie być równie intensywne we wszystkich kierunkach.

Antena nadajnika

Nie -homogeniczna połowa

Gdy medium nie jest jednorodne, prędkość propagacji fali jest inna w różnych kierunkach.

Przykładem niehomogenicznego pożywki jest atmosfera, w której istnieją różnice ciśnienia z wysokością i istnieją gradienty temperatury. Innym przykładem są warstwy skorupy ziemskiej, które różnią się gęstością i modułem sprężystym. 

Nie homogeniczność powoduje, że fronty falowe pochodzą z centralnego źródła punktualnego nie są koncentrycznymi kulami, ponieważ odległość przebywająca przez falę, w tym samym okresie czasu, jest różna w każdym kierunku.

Następnie istnieje trzywymiarowa fala, której przód fali nie jest sferyczny.

Intensywność i energia fali sferycznej

Możemy napisać wyrażenie sferycznej fali harmonicznej:

g (r, t) = (g_albo / r) cos (k⋅r - ω⋅t)

Gdzie fronty falowe rozprzestrzeniają się szybko równe:

V = ω/k

A jego amplituda maleje wraz z odwrotnością odległości R punktualnego źródła fal sferycznych.

Fale harmoniczne mają gęstość energii (Energia na jednostkę objętości) ε podane przez:

ε = ½ ρ ω² (G_albo / R)²

W tym równaniu:

-ρ Ma jednostki masy na jednostkę objętości i reprezentuje gęstość medium, w której propaguje się fala dźwiękowa.

-G_albo Jest to amplituda przemieszczenia elementu pożywki, na przykład płyn, z powodu fali propagacji.

Może ci służyć: tarcie lepkie (siła): współczynnik i przykłady

Należy zauważyć, że ponieważ jest to fala sferyczna, gęstość energii maleje wraz z odwrotnością kwadratu odległości.

Intensywność fali, to znaczy energia przenoszona na jednostkę czasu wynosi:

I = v⋅ε

Jak zawsze, w praktyce najważniejszą wielkością jest moc przekazywana na jednostkę powierzchni do odległości promieniowej R:

P = v⋅ε = i_albo / R²

Istnienie Siema_albo = ½ ρ v ω² G_albo².

Całkowita energia przekazywana na jednostkę czasu przez promień r to:  Pienka²= 4π⋅i_albo, I zgodnie z oczekiwaniami nie zależy to od odległości promieniowej. 

Przykłady trzech wymiarów fal

Trzy -wymiarowe fale są bardzo częste, więc mamy:

Anteny emitera fali elektromagnetycznej

Fale wytwarzane przez antenę lub dźwięk wytwarzany przez podstrunnicę to trzy wymiarowe fale, choć o różnej naturze

Obejmują bardzo szerokie spektrum, od fal radiowych między setkami kHz i setkami MHz, po fale emitowane przez antenę anteny Wifi Zakonu GHZ, który już wpadł w zakres mikrofalów. 

Wiemy, że kuchenka mikrofalowa, chociaż nie są promieniowaniem jonizującym, są w stanie zwiększyć temperaturę organizmu, ponieważ zawiera dużo wody.

Dlatego nie wskazane jest posiadanie anteny Wi-Fi w pobliżu głowy lub ciała. Po prostu odejdź trochę, ponieważ w podwójnej odległości intensywność to jedna czwarta.

Fale sejsmiczne

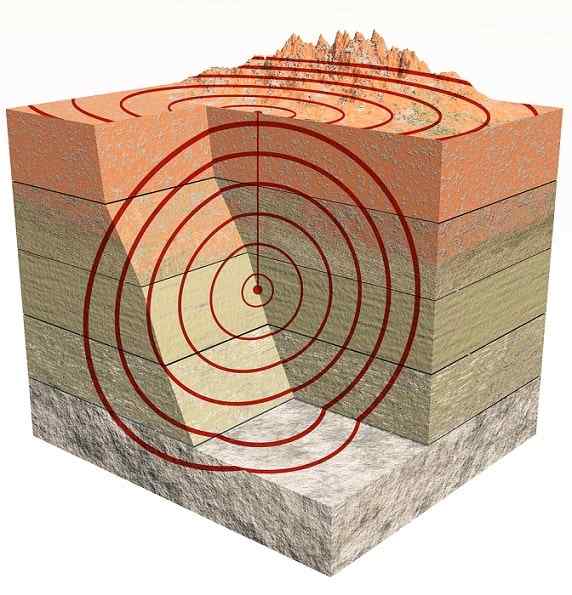Fale sejsmiczne

Są też trzy -wymiarowe fale. Głównie są takie typowe P które są falami i typami kompresyjnymi S Co to jest cięcie lub ścinanie (sSłyszeć po angielsku).

Fale P lub pierwszorzędne są pierwsi, ponieważ rozprzestrzeniły się szybciej niż fale S lub wtórne.

Dźwięk

Dźwięk przez mówienie

Dźwięk to trzywymiarowy typ fali. Fale te rozprzestrzeniły się we wszystkich kierunkach, chociaż, jak powiedzieliśmy wcześniej, nie z taką samą intensywnością we wszystkich kierunkach.

Dzieje się tak, ponieważ źródło dźwięku nie zawsze emituje z doskonale kulistą symetrią.

Bibliografia

1. Baranek, L. 1969. Akustyka. 2. Wydanie. McGraw Hill.
2. Griffiths g. Fale liniowe i nieliniowe. Odzyskane z: Scholarpedia.org.
3. Nottoli, h. 2004. Fizyka zastosowana do architektury. Nobuko.
4. Whitham g.B. 1999. Fale liniowe i nieliniowe. Wiley. 
5. Wikiwaves. Fale nieliniowe. Odzyskane z: Wikiwaves.org