Liczby transcendentne, które są formułami, przykładami, ćwiczeniami

liczby transcendentne Są to te, których nie można uzyskać w wyniku równania wielomianowego. Przeciwieństwem transcendentnej liczby jest Numer algebraiczny, które są rozwiązaniami równania wielomianowego typu:

Do_N X^N + Do_N-1 X^N-1 +… + A₂ X² + Do₁ x + a₀ = 0

Gdzie współczynniki_N, Do_N-1,… Do₂, Do₁, Do₀ Są to liczby racjonalne, nazywane Współczynniki wielomianowe. Jeśli liczba x jest rozwiązaniem poprzedniego równania, liczba ta nie jest transcendentna.

Rysunek 1. Dwie liczba o dużej wagi w nauce to liczby transcendentne. Źródło: Public DomeAnpartures.internet.

Przeanalizujemy kilka liczb i zobaczymy, czy są one transcendentne:

a) 3 nie jest transcendentne, ponieważ jest rozwiązaniem x - 3 = 0.

b) -2 nie może być transcendentne, ponieważ jest to rozwiązanie x + 2 = 0.

c) ⅓ To jest 3x - 1 = 0 Rozwiązanie

d) Rozwiązanie równania x² - 2x + 1 = 0 to √2-1, więc wspomniana liczba z definicji nie jest transcendentna.

e) ani √2, ponieważ jest wynikiem równania x² - 2 = 0. Przez podniesienie kwadratu √2 powoduje 2, który odejmował od 2, nie ma znaczenia do zera. Więc √2 jest liczbą irracjonalną, ale nie jest transcendentna.

[TOC]

Jakie są liczby transcendentne?

Problem polega na tym, że nie ma ogólnej zasady, aby je uzyskać (później powiemy formularz), ale niektóre z najbardziej znanych to liczba Liczba Pi i Numer Neper, oznaczone odpowiednio przez: π I I.

Liczba π

Numer π Naturalnie wydaje się, że obserwując, że matematyczny iloraz między obwodem p koła a jego średnicą D, niezależnie od tego, czy jest to małe czy duże koło, zawsze daje tę samą liczbę, nazywaną Liczba Pi:

π = P/D ≈ 314159…

Oznacza to, że jeśli średnica obwodu zostanie uznana za jednostkę pomiarową, dla wszystkich, niezależnie od tego, czy to duży, czy mały, obwód zawsze będzie wart p = 3,14… = π, Jak widać w animacji z ryc. 2.

Może ci służyć: twierdzenie Bolzano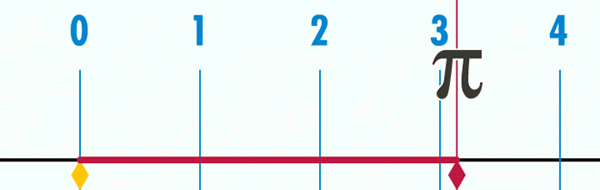Rysunek 2. Długość obwodu koła jest czasem długością średnicy, wynosi około 3,1416.

Aby określić więcej dziesiętek, musisz zmierzyć bardziej precyzję P i D, a następnie obliczyć iloraz, który został wykonany w sposób matematyczny. Wniosek jest taki, że dziesiętne iloraz nie mają końca i nigdy nie są powtarzane, więc liczba π Oprócz transcendentalnego, jest to również irracjonalny.

Irracjonalna liczba to liczba, której nie można wyrazić jako podział dwóch liczb całkowitych. 

Wiadomo, że każda transcendentna liczba jest irracjonalna, ale nie jest prawdą, że wszystkie irracjonalne są transcendentne. Na przykład √2 jest irracjonalne, ale nie jest transcendentne.

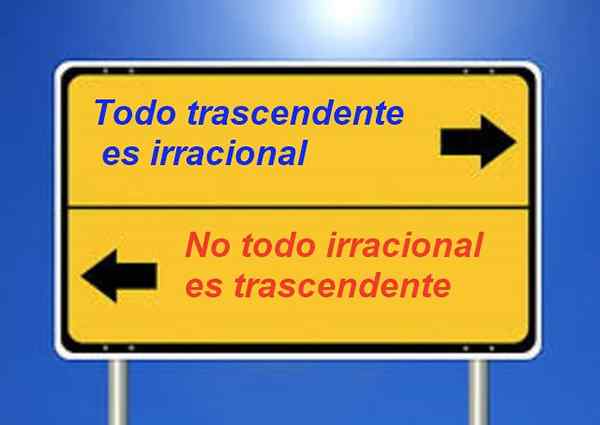Rysunek 3. Liczby transcendentne są irracjonalne, ale wzajemne stwierdzenie nie jest prawdziwe.

Liczba e

Liczba transcendentna jest podstawą neperiańskich logarytmów, a ich podejście dziesiętne to:

E ≈ 2.718281828459045235360… .

Jeśli chcesz napisać numer I Dokładnie konieczne byłoby napisanie dziesiętnych nieskończonych, ponieważ każda transcendentna liczba jest irracjonalna, jak powiedziano wcześniej.

Pierwsze dziesięć cyfr I Są łatwe do zapamiętania:

2,7 1828 1828 i chociaż wydaje się, że podąża za powtarzającym się wzorem, nie jest to osiągane w dziesiętkach rzędu większe niż dziewięć.

Bardziej formalna definicja I jest następny:

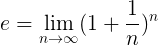
Co oznacza, że ​​dokładna wartość I Operacja wskazana w tym wzorze jest osiągana, gdy liczba naturalna N To ma tendencję do nieskończoności.

To wyjaśnia, dlaczego możemy uzyskać tylko podejście I, Ponieważ jak duża liczba n jest umieszczona, zawsze możesz znaleźć N osoby starsze.

Poszukajmy samodzielnych podejść:

-Gdy n = 100 następnie (1 + 1/100)¹⁰⁰ = 2 70481, który ledwo pokrywa się w pierwszej dziesięciu z „prawdziwą” wartością E.

-Jeśli jesteś wybrany n = 10.000 masz (1 + 1/10.000)^10.000 = 2 71815, które pokrywają się z „dokładną” wartością E w pierwszych trzech dziesiętnych dziesiętnych.

Może ci służyć: homologiczne strony

Należy zastosować ten proces, aby móc uzyskać „prawdziwą” wartość E. Nie sądzę, abyśmy mieli czas na to, ale wykonajmy jeszcze jedną próbę:

Użyjmy n = 100.000:

(1 + 1/100.000)^100.000 = 2,7182682372

Że ma tylko cztery dziesiętne, które pokrywają się z wartością uznaną za dokładną.

Ważne jest zrozumienie, że im większa wartość n wybrana do obliczenia i_N, bliżej będzie prawdziwej wartości. Ale ta prawdziwa wartość odbędzie się tylko wtedy, gdy n będzie nieskończony.

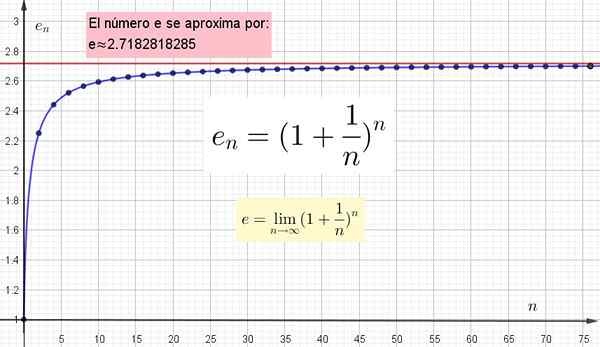Rysunek 4. Jest pokazany graficznie, ponieważ wyższa wartość n jest bliżej E, ale osiągnięcie dokładnej wartości n musi być nieskończone.

Inne transcendentne liczby

Oprócz tych słynnych liczb istnieją na przykład inne transcendentne liczby:

- 2^√2

Każda liczba algebraiczna, która nie jest 0 lub 1, podwyższona do wykładnika irracjonalnego będzie transcendentną liczbą.

-Numer 10 CHAMPERNOWNE: 

C_10 = 0,123456789101112131415161718192021… .

-Numer CHAMPERNOWNE na podstawie 2:

C_2 = 0.110111001011011… .

-Γ lub stała liczba gamma Euler-Mascheroni:

γ ≈ 0,577 215 664 901 532 860 606

To jest uzyskiwane poprzez wykonanie następujących obliczeń:

γ ≈ 1 + ½ + ⅓ + ¼ +… + 1/n - ln (n)

Gdy N Bądź bardzo duży. Mieć dokładną wartość liczby gamma, z którą można by obliczyć N nieskończony. Coś podobnego do tego, co zrobiliśmy powyżej.

I jest o wiele więcej transcendentalnych liczb. Wielki matematyk Georg Cantor, urodzony w Rosji i mieszkał w latach 1845–1918, wykazał, że zestaw liczb transcendentalnych jest znacznie większy niż zestaw liczb algebraicznych.

Wzory, w których pojawia się liczba transcendentna π

Obwód obwodu

P = π d = 2 π r, gdzie p jest obwodem, d średnica i r promień obwodu. Należy pamiętać, że:

Może ci służyć: ile musisz dodać do 3/4, aby uzyskać 6/7?

-Średnica obwodu jest najdłuższym segmentem, który łączy dwa punkty i który zawsze przechodzi przez jego centrum,

-Promień ma połowę średnicy i jest segmentem, który przechodzi od środka do krawędzi.

Obszar okręgu

A = π r² = ¼ π d²

Powierzchnia kuli

S = 4 π r^2.

Tak. Chociaż nie wydaje się, że powierzchnia kuli jest taka sama jak w czterech kręgach o tym samym promieniu co kula.

Objętość kuli

V = 4/3 π r³

Ćwiczenia

- Ćwiczenie 1

„Egzotyczna” pizzeria sprzedaje trzy średnicę pizze: 30 cm małych, mediana 37 cm i dużych 45 cm. Dziecko jest bardzo głodne i zdało sobie sprawę, że dwie małe pizze mają taki sam koszt jak duży. Co będzie dla niego lepsze, kup dwie małe pizze lub duże?

Rysunek 5.- Obszar pizzy jest proporcjonalny do kwadratu promienia, jest stałą proporcjonalności. Źródło: Pixabay.

Rozwiązanie

Im większy obszar, tym większa ilość pizzy, z tego powodu obszar dużej pizzy zostanie obliczona i w porównaniu z dwiema małymi pizzami:

Duży obszar pizzy = ¼ π d² = ¼ ⋅3,1416⋅45² = 1590,44 cm²

Mały obszar pizzy = ¼ π d² = ¼ ⋅3,1416⋅30² = 706,86 cm²

Dlatego dwie małe pizzy będą miały obszar 

2 x 706,86 = 1413,72 cm² .

Jest jasne: będzie więcej pizzy kupujących jedną dużą niż dwa małe.

- Ćwiczenie 2

„Egzotyczna” pizzeria sprzedaje również semi -man promienia 30 cm dla tego samego prostokątnego kształtu po stronie 30 x 40 cm. Które byś wybrał?

Rysunek 6.- Powierzchnia półprzewodnikowa jest dwukrotnie większa od okrągłej powierzchni podstawy. Źródło: f. Zapata.

Rozwiązanie

Jak stwierdzono w poprzednim rozdziale, powierzchnia kuli jest czterokrotnie większa niż powierzchnia okręgu o tej samej średnicy, więc półprzewodnik o średnicy 30 cm będzie miał:

30 cm Semi -Man -pizza: 1413.72 cm² (Dwa razy w okólniku o tej samej średnicy)

Prostokątna pizza: (30 cm) x (40 cm) = 1200 cm² .

Semi -man -pizza ma większy obszar.

Bibliografia

1. Fernández J. Liczba e. Pochodzenie i ciekawostki. Odzyskane z: Matematyka sojowa.com
2. Ciesz się matematyką. Numer Eulera. Odzyskane z: FaveMatimaticas.com.
3. Figuera, J. 2000. Matematyka 1st. Urozmaicony. Edycje CO-Bo.
4. Garcia, m. Liczba E w obliczeniach elementarnych. Odzyskane z: matematyki.Ciens.UCV.Iść.
5. Wikipedia. Numer PI. Odzyskane z: Wikipedia.com
6. Wikipedia. Liczby transcendentne. Odzyskane z: Wikipedia.com