Historia liczb rzeczywistej, przykłady, właściwości, operacje

liczby rzeczywiste Stanowią zestaw liczbowy, który obejmuje liczby naturalne, liczby całkowitowe, racjonalne i irracjonalne. Są oznaczone symbolem ℝ lub po prostu R A zasięg, jaki mają w nauce, inżynierii i gospodarce, jest takie, że podczas mówienia o „liczbie” prawie zakłada się, że jest to liczba prawdziwej.

Liczby rzeczywiste były używane od czasów starożytnych, chociaż nie otrzymały tej nazwy. Od czasów, gdy Pitagoras opracował swoje słynne twierdzenie, pojawiły się liczby, których nie można było uzyskać jako liczby naturalne lub liczby.

Rysunek 1. Schemat Venna pokazujący, w jaki sposób zestaw liczb rzeczywistych zawiera inne zestawy numeryczne. Źródło> Wikimedia Commons.

Przykładami liczb to √2, √3 i π. Te liczby są wywoływane irracjonalny, W przeciwieństwie do liczb racjonalnych, które pochodzą z ilorazów między liczbami całkowitymi. Konieczne było zatem zestaw liczbowy, który obejmuje oba rodzaje liczb.

Termin „liczba rzeczywista” został stworzony przez wielkiego matematyka René Descartes (1596-1650), aby rozróżnić dwa rodzaje korzeni, które mogą wynikać z rozwiązania równania wielomianowego.

Niektóre z tych korzeni mogą być parami liczb ujemnych, te Kartezjusz nazywali je „liczbami wyobrażonymi”, a tymi, którzy nie byli, były liczbami rzeczywistymi.

Nominacja utrzymywała się z czasem, powodując dwa duże zestawy numeryczne: liczby rzeczywiste i liczby złożone, szerszy zestaw, który obejmuje liczby rzeczywiste, wyobrażone i te, które są w rzeczywistości i częściowo wyobrażone.

Ewolucja liczb rzeczywistych kontynuowała swój przebieg do 1872 r Korty Dedekind. Synteza jego pracy została opublikowana w artykule, który widział światło w tym samym roku.

Może ci służyć: zwykłe wielokąty: właściwości, elementy, kąty, przykłady

[TOC]

Przykłady liczb rzeczywistych

Poniższa tabela pokazuje przykłady liczb rzeczywistych. Zestaw ten ma jako podzbiór do liczb naturalnych, liczb całkowitych, racjonalnych i irracjonalnych. Dowolna liczba tych zestawów jest sama w sobie.

Dlatego 0, negatywy, pozytywne, ułamki i dziesiętne są liczbami rzeczywistymi.

Rysunek 2. Przykładami liczb rzeczywistych są tubylcy, liczby całkowite, racjonalne, irracjonalne i transcendenci. Źródło: f. Zapata.

Reprezentacja liczb rzeczywistych na prawdziwej linii 

Liczby rzeczywiste mogą być reprezentowane na prawdziwej linii R, Jak pokazuje zdjęcie. Nie jest konieczne, aby 0 zawsze był obecny, jednak wygodnie jest wiedzieć, że negatywne reais są po lewej i po prawej stronie. Dlatego jest to doskonały punkt odniesienia.

Na prawdziwej linii zbierana jest skala, w której znajdują się liczby całkowite:… 3, -2, -1, 1, 2, 3… . Strzałka wskazuje, że linia rozciąga się na nieskończoność. Ale to nie wszystko, w żadnym rozważanym przedziale, zawsze znajdziemy nieskończone liczby rzeczywiste.

Liczby rzeczywiste są reprezentowane w porządku. Na początek istnieje kolejność liczb całkowitych, w której dodatnie.

To zamówienie pozostaje w liczbach rzeczywistych. Następujące nierówności są pokazane jako przykład:

a) -1/2 < √2

Być < π

c) π> -1/2

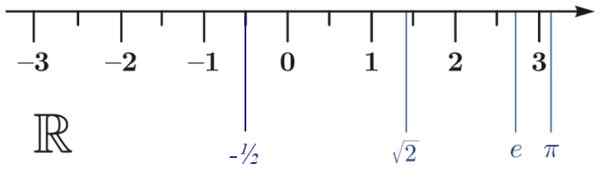Rysunek 3.- Prawdziwa linia. Źródło: Wikimedia Commons.

Właściwości liczb rzeczywistych

-Liczby rzeczywiste obejmują liczby naturalne, liczby całkowite, racjonalne i irracjonalne.

Może ci służyć: jakie są trójkątne liczby? Właściwości i demonstracje

-Własność komutatywna suma jest spełniona: kolejność dodatków nie zmienia sumy. Jeśli A i B są dwiema liczbami rzeczywistymi, zawsze prawdą jest, że:

A + B = B + A

-0 jest neutralnym elementem sumy: a + 0 = a

-Własność asocjacyjna jest spełniona dla suma. Jeśli A, B i C są liczbami rzeczywistymi: (A + B) + C = A + (B + C).

-Przeciwieństwem rzeczywistej liczby A jest -a.

-Odejmowanie jest zdefiniowane jako suma przeciwnego: a - b = a + (-b).

-Własność przemienna produktu jest spełniona: kolejność czynników nie zmienia produktu: a.B = b.Do

-Nieruchomość asocjacyjna jest również stosowana do produktu: (.B).C = a.(B.C)

-1 jest neutralnym elementem mnożenia: a.1 = a

-Własność dystrybucyjna mnożenia w odniesieniu do dodatku jest ważna: a. (b+c) = a.B + a.C

-Podział na 0 nie jest zdefiniowany.

-Dowolna liczba rzeczywisty A, z wyjątkiem 0, ma multiplikatywną odwrotność^-1 Takie, że.Do^-1 = 1.

-Jeśli a jest liczbą rzeczywistą: a⁰ = 1 i a¹ = a.

-Wartość bezwzględna lub moduł liczby rzeczywistej to odległość między wspomnianą liczbą a 0.

Operacje z liczbami rzeczywistymi

Z liczbami rzeczywistymi możesz wykonywać operacje wykonane z innymi zestawami numerycznymi, w tym sumą, odejmowaniem, mnożeniem, podziałem, ulepszeniem, promieniowaniem, logarytmami i innymi.

Jak zawsze, podział na 0 nie jest zdefiniowany, nie ma również logarytmów liczb ujemnych ani 0, chociaż prawdą jest, że log 1 = 0 i że logarytmy liczb między 0 a 1 są ujemne.

Aplikacje

Zastosowania liczb rzeczywistych do wszelkiego rodzaju sytuacji są niezwykle zróżnicowane. Liczby rzeczywiste pojawiają się w odpowiedzi na wiele problemów w naukach dokładnych, komputerowych, inżynierii, ekonomii i nauk społecznych.

Może ci służyć: Hipparco z Nicea: biografia i wkład w naukę

Wszelkiego rodzaju wielkości i kwoty, takie jak odległości, czasy, siły, intensywność dźwięku, pieniądze i wiele innych, mają swoją ekspresję w rzeczywistości.

Transmisja sygnałów telefonicznych, obraz i dźwięk wideo, temperatura klimatyzacji, grzejnik lub lodówka można kontrolować cyfrowo, co oznacza przekształcenie wielkości fizycznej w sekwencje numeryczne.

To samo dzieje się, gdy transakcja bankowa jest dokonywana online lub konsultacja komunikatów informacyjnych. Liczby rzeczywiste są wszędzie.

Ćwiczenie rozwiązane

Zobaczmy z ćwiczeniami, jak te liczby działają w wspólnych sytuacjach, w których jesteśmy codziennie.

Ćwiczenie 1

Post Office akceptuje tylko pakiety, dla których długość, plus pomiar konturu, nie przekracza 108 cali. Dlatego w przypadku akceptowanego pakietu należy spełnić, że:

L + 2 (x + y) ≤ 108

a) Czy przejdziesz paczkę o szerokości 6 cali, o wysokości 8 cali i 5 stóp długości?

b) Co powiesz na taką, która mierzy 2 x 2 x 4 stóp³?

c) Co jest najwyższe dopuszczalne dla opakowania, którego podstawa jest kwadratowa i mierzy 9 x 9 cali²?

Odpowiedz

L = 5 stóp = 60 cali

x = 6 cali

y = 8 cali

Operacja, którą należy rozwiązać, to:

L + 2 (x + y) = 60 + 2 (6 + 8) cali = 60 + 2 x 14 cali = 60 + 28 cali = 88 cali

Pakiet jest akceptowany.

Odpowiedź b

Wymiary tego pakietu są niższe niż w pakiecie A), więc oba zdołają przejść.

Odpowiedź c

W tym pakiecie:

x = l = 9 cali

Należy spełnić, że:

9+ 2 (9+ y) ≤ 108

27 + 2y ≤ 108

2Y ≤ 81

i ≤ 40.5 cali

Bibliografia

1. Carena, m. 2019. Podręcznik matematyki przednicznicy. National University of the Coast.
2. Diego, a. Liczby rzeczywiste i ich właściwości. Odzyskane z: matematyki.Un.Edu.ar.
3. Figuera, J. 2000. Matematyka 9. Stopień. Edycje CO-Bo.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Stewart, J. 2006. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.