Koncepcja liczb ujemnych, przykłady, operacje

liczby ujemne Są one po lewej stronie linii numerycznej, zawsze poprzedzone znakiem -. Za pośrednictwem negatywów można reprezentować ilości, które są poniżej lub po lewej stronie 0.

Liczby te aktywnie uczestniczą w życiu codziennym: na przykład jeśli ktoś ma dług w wysokości 5 USD, ale może zapłacić tylko 3 USD, jest winien 2 USD. Dług jest oznaczony znakiem ujemnym, aby odróżnić go od wypłaconej kwoty.

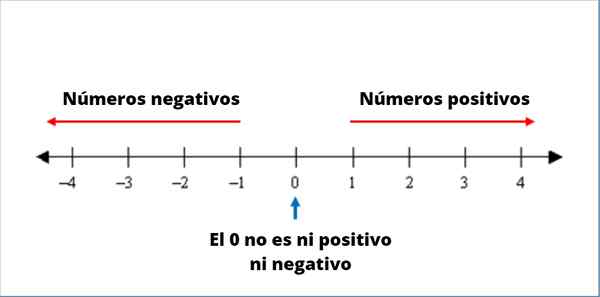
Rysunek 1. Schemat liczby negatywnych i dodatnich

Niskie pozycje na poziomie morza, temperatury poniżej temperatury zamarzania wody i podłóg niższych niż poziom ulicy można oznaczyć liczby ujemne.

[TOC]

Po co są liczby ujemne?

Istnienie negatywów rozszerza możliwe operacje numeryczne. Umieśćmy przykład odejmowania dwóch liczb. Jeśli liczby te należą do tubylców 1, 2, 3, 4, 5 ... Odejmowanie ma sens tylko wtedy, gdy odejmuje inną liczbę mniej niż on.

Wynik operacji 10–7 = 3 jest rozsądny, ponieważ zasadniczo nie możemy odebrać jednej ilości więcej niż reprezentuje.

Jednak w przypadku negatywów ta inna sytuacja zostałaby dobrze opisana: chcemy kupić coś, co jest warte 20 USD, ale mamy tylko 15 USD i poprosiliśmy o 5 USD do przyjaciela. Dług, jak powiedzieliśmy, jest oznaczony znakiem ujemnym, a zatem 15–20 = -5, który jest odczytany jako „mniej 5”.

Zestaw negatywnych liczb całkowitych powiązanych z liczbą tubylców i 0, stanowią najszerszy zestaw liczb całkowych z.

Ale negatywy mogą być również ułamkowe lub dziesiętne i należą do jeszcze szerszego zestawu: liczb rzeczywnych R, który obejmuje racjonalne i irracjonalne.

W przypadku wszystkich z nich przeprowadzane są znane operacje arytmetyczne, dbając o obsługę prostych zasad znaków, które zostały wyjaśnione poniżej.

Operacje z liczbami ujemnymi

Przed wykonywaniem operacji z liczbami ujemnymi należy ustalić pewne proste reguły, aby obsłużyć znak (-), który zawsze należy umieścić wcześniej.

Może ci służyć: różnica między wspólną frakcją a liczbą dziesiętną

Rozważ linię liczbową pokazaną na rysunku, z negatywami po lewej stronie 0 i dodatnimi po prawej stronie.

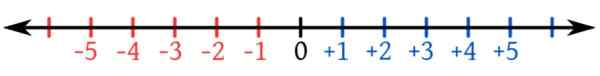Rysunek 2. Linia numeryczna z negatywami na czerwono. Źródło: Wikimedia Commons.

Strzałki linii numerycznej w obu kierunkach wskazują, że istnieją nieskończone liczby. Zauważ również, że numeryczny zestaw liczb całkowitych jest ustawiony, a każda liczba ujemna jest mniejsza niż 0 i że każdy dodatni.

Zatem -4 jest mniej niż 1, a -540 jest mniej niż 84, na przykład.

Całkowita wartość

Odległość między dowolną liczbą a 0 jest wywoływana całkowita wartość. Odległość ta jest zawsze pozytywna i oznacza w ten sposób pionowe pręty:

│-5│ = 5

│+√6│ = √6

│-3/4│ = 3/4

│-10.2│ = 10.2

To znaczy wartość bezwzględna dowolnej liczby, niezależnie od tego, czy dodatnia lub ujemna jest dodatnią liczbą liczby. Ta koncepcja będzie nam służyć później podczas pracy z liczbami ujemnymi.

Podpisać

Kolejnym bardzo ważnym szczegółem jest rozróżnienie między znakiem liczby a znakiem operacji.

Gdy liczba jest dodatnia, liczba liczby jest zwykle pomijana i rozumie się, że i tak jest ona pozytywna, ale z negatywami, które nie są możliwe, dlatego konieczne jest użycie nawiasu, zobaczmy:

-Prawidłowe: 17 - (-6) lub również +17 - (-6)

-Niepoprawnie: 17 - -6

-Niepoprawnie: -5 + +7

-Prawidłowe: - 5 + (+7) lub -5 + 7

Gdy koncepcje wartości bezwzględnej, porządku i znaczenia znaku ujemnego, możemy przejść do operacji podstawowych.

Dodatek

Rozróżniamy następujące przypadki, zaczynając od suma dwóch pozytywów, których procedura jest już bardzo znana:

-Dodaj dwie liczby dodatnie: ( + a) + ( + b) = a + b

Co oznacza, że ​​dodajemy jak zwykle, zobaczmy:

(+8) + (+5) = 8 + 5 = 13

-Dodaj dwie liczby ujemne: (-a) + (-b) =-(a + b)

W takim przypadku dodajemy wartości bezwzględne liczb i do wyniku wynika, że ​​znany jest znak ujemny, tak jak to:

Może ci służyć: rodzaje całek

(-7) + (-11) = - (7+ 11) = - 18

-Dodaj negatywne i pozytywne: ( + a) + (-B)

Dla tej operacji wartości bezwzględne są odjęte, a wynik przenosi znak liczby o najwyższej wartości bezwzględnej. Zróbmy kilka przypadków:

a) (-16) + (+3)

Odpowiednie wartości bezwzględne wynoszą 16 i 3, liczba o najwyższej wartości bezwzględnej wynosi 16, których znak jest ujemny, zatem:

(-16) + (+3) = - (16 - 3) = -13

b) (+8) + (-3) = + (8-3) = +5 = 5

Suma negatywów jest również do pracy, co oznacza, że ​​porządek w reklamach nie jest ważny dla wyniku.

Obowiązują poprzednie reguły, jeśli chcesz dodać więcej niż dwie liczby, co można wykonać z właściwością asocjacyjną: a + b + c = (a + b) + c = a + (b + c).

Przed zobaczeniem w tym przypadku najpierw zobaczmy odejmowanie dwóch liczb całkowitych.

Odejmowanie

Odejmowanie jest zdefiniowane jako suma przeciwnego. Przeciwieństwo liczby A jest -a, taka:

-4 jest przeciwieństwem + 4

½ jest przeciwieństwem -½

Jeśli poprosą nas o wykonanie odejmowania dwóch liczb, niezależnie od znaku, po prostu dodajemy przeciwieństwo drugiego:

a) (-53) -(+8) = (-53)+( -8) = -(53+8) = -61

b) (+7) - (-12) = (+7)+(+12) = 7+12 = 19

c) (+2) - (+π) = (+2)+( - π) = 2 - π

Przykład

Wykonaj następującą operację (+4) + (-7) + (+19)

Przepisujemy to w ten sposób za pomocą kwadratowych nawiasów, aby najpierw wskazać operację, którą należy wykonać:

(+4) + (-7) + (+19) = [(+4) + (-7)] + (+19) = [-(4-7)] + 19 = [-(-3)] + 19 = 19 - (-3) = 19 + (+3) = 22

Mnożenie

Zasady mnożenia jest podsumowane na poniższym rysunku:

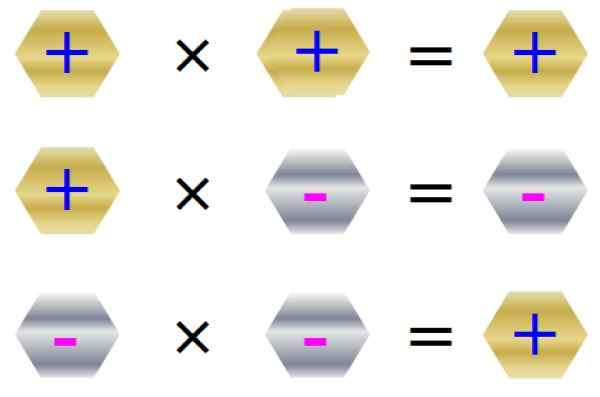Rysunek 3. Znaki reguły mnożenia. Źródło: f. Zapata.

Właściwości mnożenia

-Przekonanie: Kolejność czynników nie zmienia produktu, a zatem ≠ = B.Gdzie A i B są liczby ujemne, całościowe lub ułamkowe.

Może ci służyć: liczby irracjonalne: historia, właściwości, klasyfikacja, przykłady

-Asocjacyjność: Niech liczby A, B i C, to się spełniło (a.B). C = a. (B.C)

-Dystrybucja w odniesieniu do sumy: Niech liczby A, B i C, to ważne. (b+c) = a.B +a.C

Przykład

(-3/2) x [(-5) + (+4)-( + 2)] = (-3/2) x (-5) + (-3/2) x (+4) + (- 3/2) x (-2) = (15 - 12 + 6)/2 = 9/2

Operacja między nawiasami kwadratowymi również mogła zostać rozwiązana, a wynik pomnożony przez (-3/2), tak jak to:

(-3/2) x [-5 + 4-2] = (-3/2) x (-3) = 9/2

Dział

Zasady podziału są odsłonięte na poniższym rysunku:

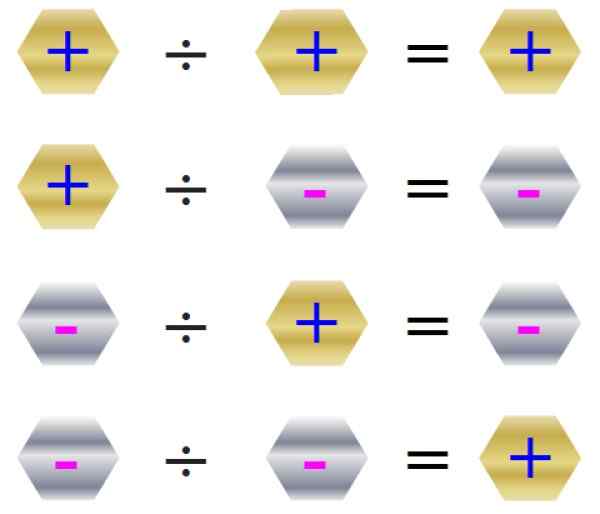Rysunek 4. Znaki reguły dla podziału. Źródło: f. Zapata.

Podział nie jest do pracy i zwykle w oru ≠ B ÷ a, nie dozwolono podziału między 0. Spójrzmy na przykład:

(-54) ÷ (+3) = -18

Aby uzyskać ten wynik, iloraz jest po prostu wykonany, a znak wybierany zgodnie z tabelą pokazaną na rysunku, która odpowiada trzeciej opcji w górę.

Potencjał

Potencjał to działanie formularza^N, Gdzie jest podstawa i n jest wykładnikiem. Podstawa i wykładnik mogą mieć dowolny znak.

-Jeśli podstawa jest ujemna lub pozytywna, a wykładnik jest całość, wynik operacji jest zawsze dodatni.

-Gdy podstawa jest dodatnia, a wykładnik jest całkowicie wynikowy.

-A jeśli podstawa jest ujemna, a wykładnik jest dziwny, wynik jest ujemny.

Wykładniki ułamkowe zostaną wyrażone na przemian jako root, na przykład pierwiastek kwadratowy równoważny frakcyjnego wykładnika ½, korzeń sześcienny równa się wykładnikowi 1/3 i tak dalej.

Spójrzmy na kilka przykładów:

a) (-3)³ = (-3) x (-3) x (-3) = -27

b) 16 ^-1/2 = 1 / √16 = ¼

c) (+8) ^1/3 = korzeń sześcienny 8 = 2

Bibliografia

1. Baldor, a. 1986. Arytmetyka. Codex Editions and Dystrybucje.
2. Figuera, J. 2000. Matematyka 7. Stopień. Edycje CO-Bo.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Matematyka jest zabawna. Jak dodać i odjąć liczby pozytywne i ujemne. Odzyskany z: Mathisfun.com
5. Wikipedia. Liczby ujemne. Odzyskane z: jest.Wikipedia.org.