Historia liczb irracjonalnych, właściwości, klasyfikacja, przykłady

Irracjonalne liczby Są tymi, których ekspresja dziesiętna ma nieskończone postacie bez powtarzającego się wzorca, dlatego nie można ich uzyskać, czyniąc iloraz między dowolnymi dwoma liczbami całkowitych.

Wśród najbardziej znanych irracjonalnych liczb są:

Rysunek 1. Od góry do dołu następujące irracjonalne liczby: PI, liczba Eulera, Aúrea i dwa korzenie kwadratowe. Źródło: Pixabay.

Wśród nich bez wątpienia π (pi) jest najbardziej znane, ale jest ich wiele innych. Wszystkie należą do zestawu liczb rzeczywistych, który jest zestawem liczbowym, który łączy racjonalne i irracjonalne liczby.

Punkty zawiesinowe na rycinie 1 wskazują, że dziesiętne podążają za w nieskończoność, to, że przestrzeń obecnych kalkulatorów pozwala tylko pokazać kilka.

Jeśli spojrzymy uważnie, pod warunkiem, że dokonamy iloraz między dwoma liczbami całkowitych, uzyskuje się dziesiętne z ograniczonymi liczbami lub jeśli nie, z nieskończonymi liczbami, w których jeden lub więcej jest powtarzane. Cóż, nie dzieje się tak z irracjonalnymi liczbami.

[TOC]

Historia liczb irracjonalnych

Wielki matematyk starożytności Pitagoras, urodzony w 582.C w Samos, Grecja, założyła Pitagorean School of Myśli i odkryła słynne twierdzenie, które nosi jego imię. Mamy go w lewo (Babilończycy mogli go już poznać długo).

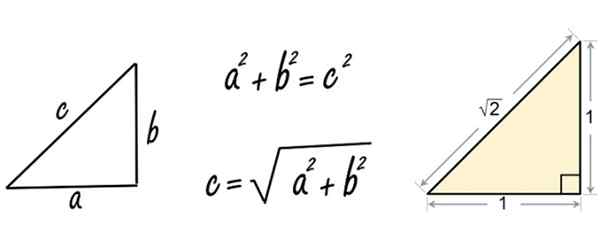Rysunek 2. Twierdzenie Pitagorasa dotyczyło trójkąta boków równych 1. Źródło: Pixabay/Wikimedia Commons.

Cóż, kiedy Pitagoras (lub prawdopodobnie jego uczeń) zastosował twierdzenie do prawego trójkąta stron równych 1, znalazł liczbę irracjonalną √2.

Może ci służyć: linie suszenia

Zrobił to w ten sposób:

C = √1² + 1² = √1+1 = √2

I natychmiast zdał sobie sprawę, że ta nowa liczba nie pochodzi z ilorazu między dwiema innymi liczbami naturalnymi, które były znanymi w tym czasie.

Dlatego nazwał go irracjonalny, A odkrycie spowodowało wielki niepokój i zamieszanie wśród Pitagorejczyków.

Właściwości irracjonalnych liczb

-Zestaw wszystkich irracjonalnych liczb jest oznaczony literą I, a czasem jak Q* lub Q^C. Związek między liczbami irracjonalnymi I lub Q* a liczbami racjonalnymi q, powoduje powstanie zestawu rzeczywistych liczb n.

-Przy liczbach irracjonalnych można wykonać znane operacje arytmetyczne: suma, odejmowanie, mnożenie, podział, potencjał i nie tylko.

-Podział między 0 nie jest zdefiniowany wśród irracjonalnych liczb.

-Suma i produkt między liczbami irracjonalnymi niekoniecznie są kolejną liczbą irracjonalną. Na przykład:

√2 x √8 = √16 = 4

A 4 nie jest liczbą irracjonalną.

-Jednak suma liczby racjonalnej plus irracjonalna powoduje irracjonalne. Tą drogą:

1 + √2 = 2.41421356237…

-Produkt innej liczby racjonalnej od 0 według liczby irracjonalnej jest również irracjonalny. Spójrzmy na ten przykład:

2 x √2 = 2.828427125…

-Odwrotność irracjonalnych powoduje inną irracjonalną liczbę. Spróbujmy trochę:

1 / √2 = 0.707106781…

1 / √3 = 0.577350269…

Liczby te są interesujące, ponieważ są również wartościami niektórych trygonometrycznych przyczyn znanych kątów. Wiele przyczyn trygonometrycznych to liczby irracjonalne, ale istnieją wyjątki, takie jak Sen 30º = 0.5 = ½, co jest racjonalne.

-Podsumowując, właściwości przemienne i asocjacyjne są spełnione. Jeśli A i B są dwiema irracjonalnymi liczbami, oznacza to, że:

Może Ci służyć: funkcja zatrzymywania: definicja, właściwości, przykłady

A + B = B + A.

A jeśli C jest kolejną liczbą irracjonalną, to:

(A + B) + C = A + (B + C).

-Własność dystrybucyjna mnożenia w odniesieniu do sumy to inna znana właściwość, która jest również spełniona dla liczb irracjonalnych. W tym przypadku:

Do.(b+c) = a.B + a.C.

-Irracjonalny ma coś przeciwnego: -a. Po dodaniu wyniku wynosi 0:

A+(-a) = 0

-Pomiędzy dwoma różnymi racjonalnymi, istnieje co najmniej jedna liczba irracjonalna.

Lokalizacja irracjonalnego numeru na prawdziwej linii

Rzeczywista linia to linia pozioma, w której znajdują się liczby rzeczywiste, z których ważna jest irracjonalna.

Aby znaleźć irracjonalną liczbę na prawdziwej linii, w formie geometrycznej, możemy być warte twierdzenia Pitagoras, reguły i kompasu.

Jako przykład zlokalizujemy √5 na prawdziwej linii, dla której rysujemy prostokątny trójkąt boków x = 2 I y = 1, Jak pokazuje zdjęcie:

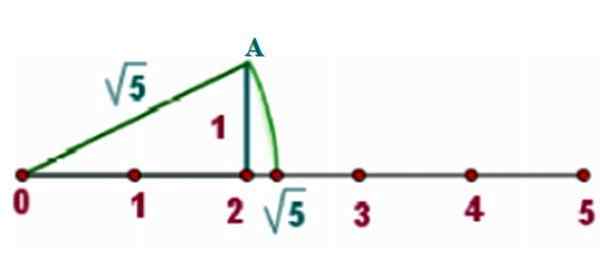Rysunek 3. Metoda lokalizacji irracjonalnej liczby na prawdziwej linii. Źródło: f. Zapata.

W przypadku twierdzenia Pitagorasa hipotenusa takiego trójkąta jest:

C = √2² + 1² = √4+1 = √5

Teraz rytm z końcówką jest umieszczony w 0, gdzie jest również jeden z wierzchołków prawego trójkąta. Czubek ołówka kompasu musi znajdować się w wierzchołku.

Narysowany jest łuk obwodu, który przecina prawdziwą linię. Ponieważ odległość między środkiem obwodu a dowolnym punktem tego samego jest promień, który jest wart √5, punkt przecięcia wynosi również √5 od środka.

Wykresu widać, że √5 wynosi od 2 do 2.5. Kalkulator oferuje nam przybliżoną wartość:

Może ci służyć: współczynnik determinacji: wzory, obliczenia, interpretacja, przykłady

√5 = 2.236068

I tak, budując trójkąt z odpowiednimi stronami, można zlokalizować inne irracjonalne, takie jak √7 i inne.

Klasyfikacja liczb irracjonalnych

Irracjonalne liczby są podzielone na dwie grupy:

-Algebraiczny

-Transcendentne lub transcendentalne

Liczby algebraiczne

Liczby algebraiczne, które mogą być irracjonalne lub nie, są rozwiązaniami równań wielomianowych, których ogólną formą jest:

Do_N X^N + Do_N-1X^N-1 + Do_N-2X^N-2 +.. . +Do₁x + a_albo = 0

Przykładem równania wielomianowego jest takie równanie drugiego stopnia:

X³ - 2x = 0

Łatwo jest wykazać, że liczba irracjonalna √2 jest jednym z roztworów tego równania.

Liczby transcendentne

Zamiast tego liczby transcendentne, choć irracjonalne, nigdy nie powstają jako rozwiązanie równania wielomianowego.

Liczby transcendentne występujące najczęściej w stosowanej matematyce są π, ponieważ ich związek z obwodem i liczbą E lub liczbą Eulera, co jest podstawą neperowskich logarytmów.

Ćwiczenia

Na czarnym kwadratu umieszczono szarość w pozycji wskazanej na rysunku. Wiadomo, że powierzchnia czarnego kwadratu wynosi 64 cm². Ile kosztuje długości obu kwadratów?

Rysunek 4. Dwa kwadraty, z których można znaleźć długość boków. Źródło: f. Zapata.

Odpowiedź

Powierzchnia kwadratu z boku L to:

A = l²

Ponieważ czarny plac ma 64 cm² obszaru, jego strona musi wynosić 8 cm.

Ta miara jest taka sama jak Przekątna szare. Stosując twierdzenie Pitagorasa do tej przekątnej i pamiętając, że boki kwadratowe tak samo, będziemy mieli:

8² = L_G² + L_G²

Gdzie l_G To jest bok szarego kwadratu.

Dlatego: 2l_G² = 8²

Zastosowanie pierwiastka kwadratowego po obu stronach równości:

L_G = (8/√2) cm

Bibliografia

1. Carena, m. 2019. Podręcznik matematyki przednicznicy. National University of the Coast.
2. Figuera, J. 2000. Matematyka 9. Stopień. Edycje CO-Bo.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Portal edukacyjny. Irracjonalne liczby i ich właściwości. Pobrano z: Portaleeducative.internet.
5. Wikipedia. Irracjonalne liczby. Odzyskane z: jest.Wikipedia.org.