Liczby nieparzyste

Co to są liczby nieparzyste?

liczby nieparzyste Są to liczby całkowitym, które nie są podzielne przez 2. Oznacza to, że przy dziwnych ilościach nie możesz na przykład tworzyć grup 2, jeśli ktoś ma 9 cukierków do podzielenia się z przyjacielem i nie chce ich dzielić, dotknie 4 cukierków, a pozostałe 5.

Niektóre liczby nieparzyste są następujące: ... -5, -3, -1, 1, 3, 5, 7, 9, 11, 13 ..  W tym wyrażeniu punkty zawiesinowe wskazują, że istnieje więcej liczb, zarówno w lewo, jak i w prawo.

Rysunek 1: Jak wiedzieć, czy liczba jest dziwna?

Patrząc uważnie, widać, że każdą liczbę nieparzysty można uzyskać, dodając 2 do poprzedniej liczby. Na przykład, jeśli dodamy 2 do -1, otrzymasz 1, jeśli wykonamy 1 + 2, to 3 i tak dalej.

Obserwuje się również, że jeśli pary są przeplatane, w tym 0, co jest uważane za liczbę parzystą, otrzymywany jest zestaw liczb całkowitych Z.

Dlatego każda dziwna liczba naturalna może być napisana w postaci 2n + 1, gdzie n = 0, ± 1, ± 2, ± 3, ± 4, ± 5…, gdzie symbol ± oznacza, że ​​można ją uznać za dodatnie lub jako negatywny.

W przypadku większych liczb można go rozpoznać, gdy jest to dziwne, ponieważ zawsze kończy się na 1, 3, 5, 7 lub 9. Na przykład 1571 jest dziwne, podobnie jak negatywna liczba całkowita -152.489.

Przykłady liczb nieparzystych

Liczby nieparzyste są często prezentowane w naturze, a wśród nich liczba 3 ma szczególne znaczenie. Spójrzmy na kilka przykładów:

-Istnieje wiele kwiatów z nieparzystą liczbą płatków.

-Mamy 5 palców z każdej ręki.

Może ci służyć: zmienna losowa: koncepcja, typy, przykłady

-Ludzie mają 23 pary chromosomów.

-Istnieją 3 prawa Newtona i 3 prawa termodynamiki.

-Jądra atomów, które mają nieparzystą liczbę protonów i neutronów, są mniej stabilne niż te z liczbą pary.

-Mędrcy mają 3.

-W opowieściach i opowiadaniach często pojawia się numer 3, na przykład powieści, takie jak Trzej muszkieterowie autor: Alejandro Dumas i w popularnych historii, takich jak Trzej bracia I Trzy małe świnki.

-Dla kompozycji artystycznej jest wezwanie Dziwna reguła, który ustala, że ​​kompozycja o nieparzystych liczbie elementów jest bardziej atrakcyjna niż jeden z parą. Liczba nieparzystna dodaje dynamizm, a jedna para zapewnia stabilność.

Rysunek 2. Nieparzystą liczbę elementów dodaje dynamizmu do obrazu

-Powszechną strategią, aby ceny obiektów wyglądały tańsze, jest skończenie 9, na przykład 2.99 USD, 39 USD i tak dalej.

-Numer 13 jest przez niektórych uważany za pecha, podczas gdy inne przypisują mistyczne cechy 11, oba liczby nieparzyste.

Liczby Primo

Liczby Primo, ci, którzy przyznają się tylko do sami dzielnicy i 1, są dziwne, z wyjątkiem 2, co jest jedynym momentem liczbowym kuzyna.

Możliwe jest wykazanie, że dowolna liczba może zostać rozbita jako produkt czynników podstawowych (w tym tych mocy) i że ten sposób wyrażania liczby jest unikalny, z wyjątkiem kolejności czynników.

Na przykład liczba 45 można rozbić jako 45 = 3³ x 5.

Operacje liczb nieparzystych

Przy liczbach nieparzystych przeprowadzane są wszystkie operacje arytmetyczne, a niektóre mają wyjątkowe cechy.

Może ci służyć: symbolizacja wyrażeń

- Sum i produkty

-Suma dwóch liczb nieparzystnych powoduje liczbę parzystą: 3+5 = 8; 11+15 = 26; (-10)+ (+6) = - 4.

-Dodając liczbę nieparzystą z jednym momentem obrotowym, wynik jest nieparzysty: 7+2 = 9; 26+ 9 = 35; (-5) + 12 = 7.

-Jeśli N Pierwsze liczby naturalne, dziwne i kolejne N². Zobaczmy to z nieco więcej szczegółów:

Dla n = 2: 1 + 3 = 4 = 2²

Dla n = 3: 1 + 3 + 5 = 9 = 3²

Dla n = 4: 1 + 3 + 5 + 7 = 16 = 4²

-Gdy nieparzyste jest mnożone przez parę, pochodzi równa liczba: 7 x 4 = 28; (-3) x 12 = -36.

-Mnożenie dwóch liczb nieparzystnych uzyskuje się również nieparzyste: 3 x 5 = 15; (-5) x (+11) = -55.

- Uprawnienie

-Gdy liczba dodatnia jest podniesiona do dziwnej mocy, jest to liczba dodatnia, na przykład: 3³ = 27.

-Podnosząc liczbę ujemną do dziwnej mocy, wynik jest ujemny: (-2)³= (-2) x (-2) x (-2) = -8.

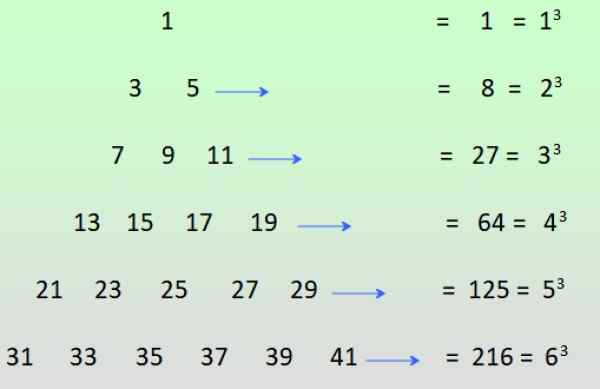
-Dziwne moce dodatnich liczb całkowitych można osiągnąć, jeśli liczby nieparzyste są dostępne, jak pokazano na rysunku i dodano wiersze:

Rysunek 3. Uzyskanie dziwnych mocy z sumy liczb nieparzystych. Źródło: f. Zapata.

Rozwiązane ćwiczenia

- Ćwiczenie 1

Zdecyduj, czy wynik następującej operacji jest równy, czy dziwny:

(53476890083 + 1987628967) x 13567903

Rozwiązanie

Aby uzyskać odpowiedź, nie musisz biegać, aby szukać kalkulatora, ale aby zastosować widoczne właściwości. Spójrzmy na ostatnie cyfry dodatków, które wynoszą odpowiednio 3 i 7:

53476890083  + 1987628967

Oznacza to, że uzależnieni są dziwni i wiemy już, że suma dwóch nieparzystych liczb jest równa.

Dlatego liczba wynikająca z nawiasu jest równa i pomnożymy liczbę, która kończy się na 3:

Może ci służyć: algebra wektorowa

13567903

Co oznacza, że ​​liczba ta jest dziwna.

We właściwościach opisanych powyżej ustalono, że pomnożenie momentu obrotowego x jest liczbą parzystą. Dlatego wynikowa operacja jest równa.

- Ćwiczenie 2

Ile kosztuje suma pierwszych 5 kolejnych liczb nieparzystego? I z pierwszych 50?

Rozwiązanie

Suma pierwszych 5 kolejnych liczb nieparzystego to:

1 + 3 + 5 + 7 + 9 = 25

Ale jeśli chcemy dodać pierwsze 50 w ten sposób, jest to kłopotliwe, więc idziemy do właściwości. Potwierdzają, że suma kolejnych liczb nieparzystych wynosi n². W takim przypadku n = 50, a żądana suma to:

pięćdziesiąt² = 50 x 50 = 2500.

- Ćwiczenie 3

Po dodaniu trzech kolejnych liczb nieparzystych uzyskano 237. Jakie są liczby?

Rozwiązanie

Nazwijmy nasz pierwszy nieparzysty numer, a drugi i Z do trzeciego, zgodnie z stwierdzeniem, że jest spełnione, że:

x + y + z = 237

W języku algebraicznym dowolna liczba nieparzysty może być napisana w postaci 2n +1. Zróbmy naszą pierwszą nieparzystą liczbę:

x = 2n +1

Dodajmy 2, aby uzyskać następujące dziwne:

y = x + 2 = (2n + 1) + 2 = 2n + 3

I wreszcie jest dodawany ponownie 2, aby uzyskać trzeci nieparzysty:

Z = (2n +3) + 2 = 2n + 5

Wszystko to dodaje:

2n + 1 + 2n + 3 + 2n + 5 = 237

6n + 9 = 237

Powoduje to proste równanie liniowe, którego rozwiązaniem jest:

n = 38

A teraz z wartością n = 38 są trzy zamówienia:

x = (2 × 38) + 1 = 77

Dlatego następujące są dziwne:

y = 79

Z = 81

A czytelnik może łatwo sprawdzić, czy suma trzech wynosi 237.

Bibliografia

1. Baldor, a. 1986. Arytmetyka. Codex Editions and Dystrybucje.
2. Dzielnice, l. Liczby nieparzyste i moce liczb naturalnych. Pobrano z: Sinewton.org.
3. Genialny. Liczby nawet i nieparzyste. Odzyskane od: genialne.org.
4. Matematyka 18. Operacje liczb nieparzystych. Źródło: Mathematics18.com.
5. Wikipedia. Liczby nawet i nieparzyste. Odzyskane z: jest.Wikipedia.org.